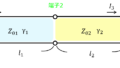
下図のように
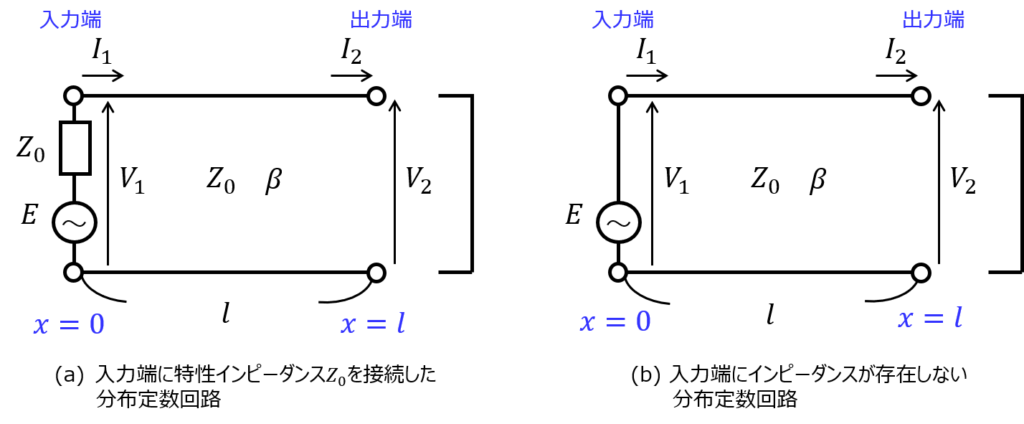
(a) 入力端に特性インピーダンス\(Z_{0}\)を接続した分布定数回路
(b) 入力端にインピーダンスが存在しない分布定数回路
を考える。
電圧源Eを入力端に接続し、出力端を(i)開放、(ii)短絡する。
\(0≦x≦l\)の範囲における電圧、電流の時間変化を(a)(b)の場合それぞれ求めよ。
ただし、伝搬速度を\(v\)とし、回路は無損失とする。
はじめに
今までの記事にて、分布定数回路の問題を複数紹介してきました。しかし、全て定常状態の前提でのお話でした。本記事では、過渡状態における考え方を紹介します。
本記事で覚えたいこと
- 分布定数回路の過渡現象は、ある時間における波の重ね合わせで考える。
- \(t=0\)のとき、入力端での電圧、電流を求める。(入力波)
- \(0≦t≦\dfrac{l}{v}\)のとき、2.で求めた電流、電圧が\(x=vt\)まで伝搬する。
- \(t=\dfrac{l}{v}\)のとき、出力端の反射係数に基づき、入力波と反射波を重ね合わせる。
- \(t=\dfrac{2l}{v}\)のとき、入力端の反射係数に基づき、入力波と反射波を重ね合わせる。
- \(t=\dfrac{3l}{v}\)のとき、出力端の反射係数に基づき、同じことを繰り返す。
以前の記事でお話しした通り、分布定数回路は、集中定数回路のように短い距離を想定していません。長い距離を想定しているため、出力端まで電流、電圧が届くまでに時間があります。
出力端まで届いたときも、それで定常状態になるわけではありません。反射係数が0でないとき、反射波が発生します。これにより、入射波と反射波の重ね合わせが発生し、波の大きさは変化します。
これが、反射波が0になるまで減衰するまで続きます。
反射係数が\(|\Gamma|<1\)のときは、反射波が入射波に対し\(\Gamma\)倍することを繰り返すので、いずれ0に収束します。
しかし、反射係数が\(|\Gamma|=1\)のときは、反射波の絶対値は入力波と同じのため、計算収束しません。これを、次章で見ていきます。
解答例
(a) 入力端に特性インピーダンス\(Z_{0}\)が接続されているとき
入力端の電圧反射係数は\begin{eqnarray}|\Gamma_{0}|=\dfrac{Z_{0}-Z_{0}}{Z_{0}+Z_{0}}=0\end{eqnarray}
です。これに対し、出力端の反射係数は、(i)開放 (ii)短絡 で変わります。
それぞれの振る舞いを下記で見ていきましょう。
(i) 出力端を開放したとき
出力端の電圧反射係数は、\(Z=∞\)なので、\begin{eqnarray}|\Gamma_{l}|=\dfrac{Z-Z_{0}}{Z+Z_{0}}=1\end{eqnarray}である。
\(t=0\)のとき、入力端に接続している特性インピーダンス\(Z_{0}\)と分布定数回路の特性インピーダンス\(Z_{0}\)の直列接続と考える。入力端に入射する波(電圧\(v\)、電流)\(i\)は、下記で与えられる。
\begin{align} &v=\dfrac{Z_{0}}{Z_{0}+Z_{0}}E=\dfrac{E}{2Z_{0}} \\ &i=\dfrac{E}{2Z_{0}} \end{align}

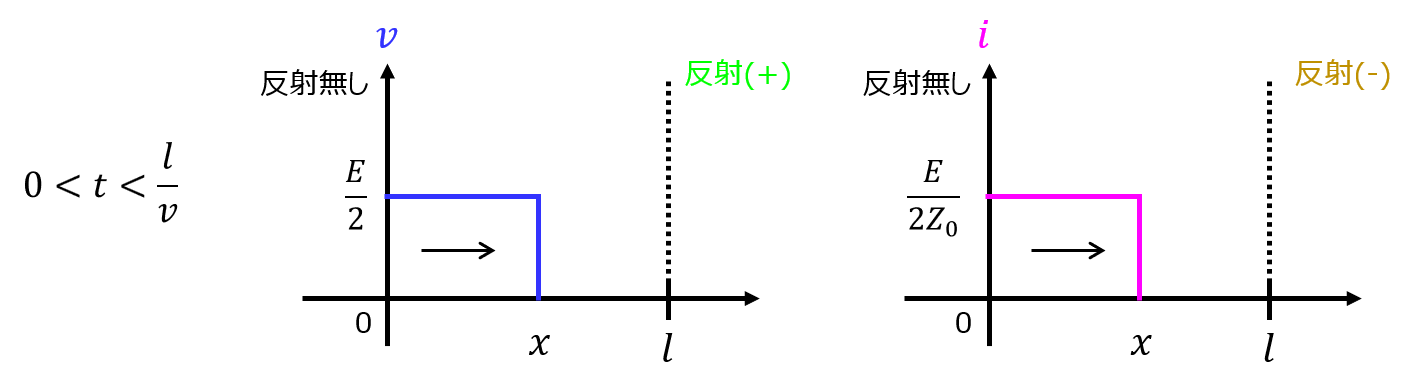
これが、出力端まで到達する\(0<t<\dfrac{l}{v}\)まで、位置\(x=vt\)まで伝搬する。
次に、\(\dfrac{l}{v}<t<\dfrac{2l}{v}\)を考える。出力端の電圧反射係数1なので、入射波と同じ位相、大きさの反射波が発生する。よって、入力波と反射波を重ねた波(電圧)は入力波の2倍になる。
一方で、電流の場合を考える。出力端は開放されているため、反射波(電流)は発生しない。\(I=0\)になるため、位相が入力波と逆の反射波が発生する。
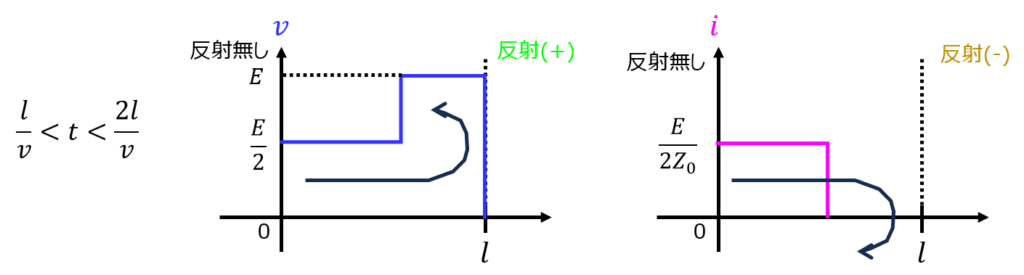
最後に、\(\dfrac{2l}{v}<t\)を考える。反射波が入力端まで到達した後である。電圧反射係数が0のため、これ以上反射波は発生しない。
よって、定常状態となり、以下のように図示できる。
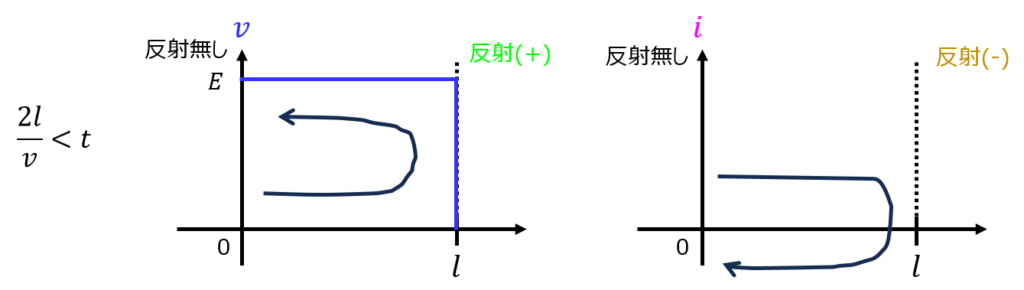
全区間\(0≦x≦l\)において、電圧は\(E\)、電流\(I\)は0。
(ii) 出力端を短絡したとき
出力端の反射係数が変化し、
\begin{eqnarray}|\Gamma_{l}|=\dfrac{0-Z_{0}}{0+Z_{0}}=-1\end{eqnarray}
となり、\(\dfrac{l}{v}<t<\dfrac{2l}{v}\)以降の波形が変わります。
\(0<t<\dfrac{l}{v}\)のとき、(i)と同じ

\(\dfrac{l}{v}<t<\dfrac{2l}{v}\)のとき、反射波(電圧)は入力波と逆の位相で同じ大きさで発生する。
一方で、反射波(電流)は、入力波と同じ位相で同じ大きさで発生する。
よって、入力波と反射波を重ね合わせた合成波(電圧)は0。合成波(電流)は入力波の2倍になる。
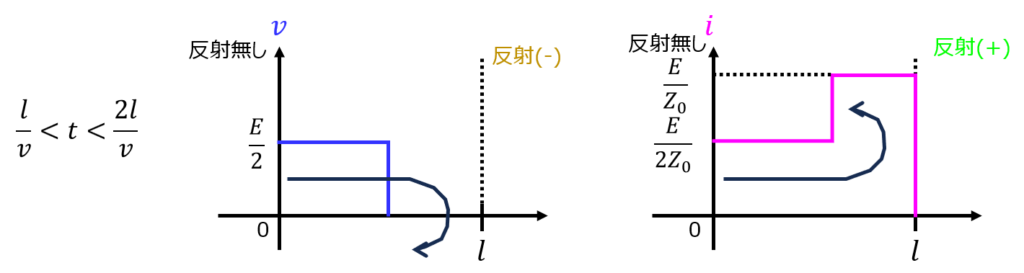
\(\dfrac{2l}{v}<t\)のとき、定常状態となり、下記の図になる。

このように、(i)と(ii)で電圧と電流の関係が逆になることが分かりました。
(b) 入力端にインピーダンスが存在しないとき
入力端の電圧反射係数は、\begin{eqnarray}\Gamma_{0}=\dfrac{0-Z_{0}}{0+Z_{0}}=-1\end{eqnarray}
前節より、出力端を (i)開放 (ii)短絡 にしたとき、それぞれの反射係数は\(\Gamma=1,-1\)になります。絶対値を取ると1のため、ある値に収束しないことが予想されます。
(i) 出力端を開放したとき
入力端は、\(\Gamma_{0}=-1\)、出力端は、\(\Gamma_{l}=1\)のため入力波の増幅と打消しを繰り返す。
\(0<t<\dfrac{l}{v}\),\(\dfrac{l}{v}<t<\dfrac{2l}{v}\)までは、(a)(i)と同じ。
ただし、\(t=0\)での入力端における電圧、電流は、特性インピーダンス\(Z_{0}\)が無くなった分2倍になる。
\begin{align}&v=\dfrac{Z_{0}}{Z_{0}}E=\dfrac{E}{Z_{0}} \\ &i=\dfrac{E}{Z_{0}} \end{align}
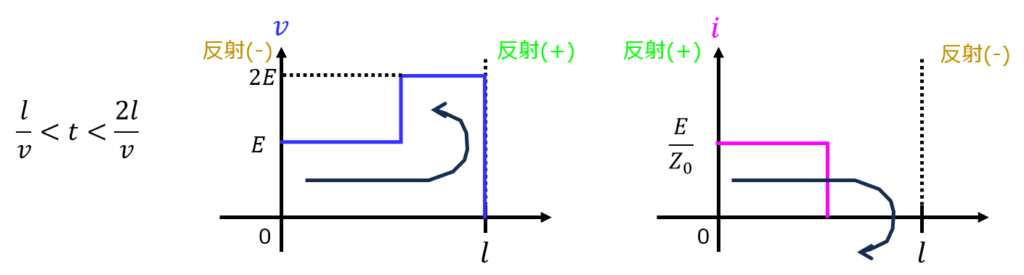
\(\dfrac{2l}{v}<t<\dfrac{3l}{v}\)のとき、入力端で逆向きの位相の反射波(電圧)が発生する。このため、入力波に対して反射波は打ち消しあう。
一方で、電流の場合は同じ位相のため、増幅し合う。
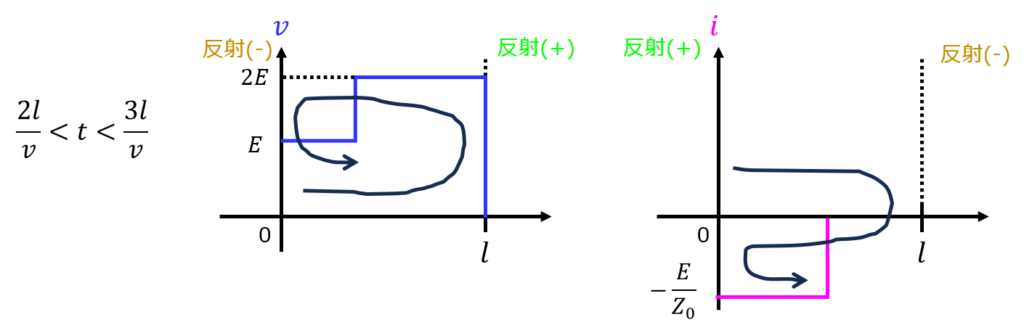
\(\dfrac{3l}{v}<t<\dfrac{4l}{v}\)のとき、
出力端で波の反射が発生する。入力波(電圧)を増幅する。負の方向のため、反射波も負
入力波(電流)は打ち消し合うため、以下のような波形になる。
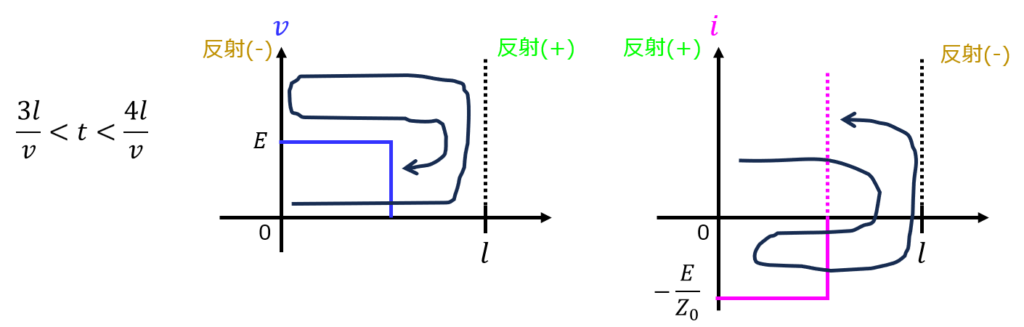
\(\dfrac{4l}{v}<t<\dfrac{5l}{v}\)のとき、\(0<t<\dfrac{l}{v}\)と同じになります。
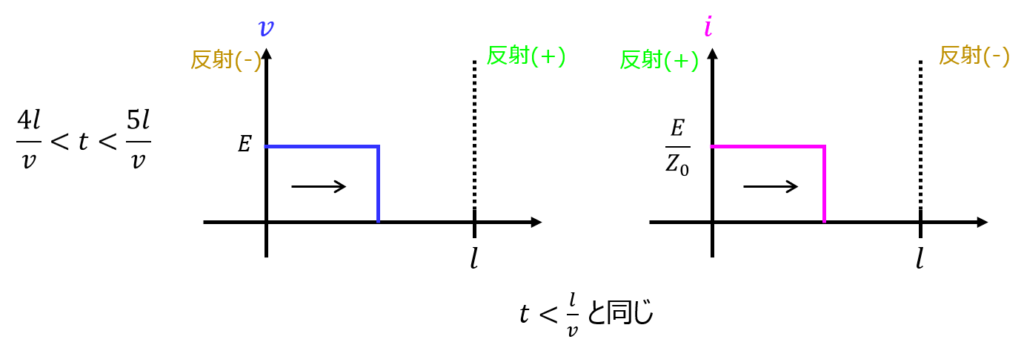
以降、上記を繰り返します。
(ii) 出力端を短絡したとき
入力端は、\(\Gamma_{0}=-1\)、出力端は、\(\Gamma_{l}=-1\)になる。
入力波(電圧)は、増幅と打消しを繰り返す。
入力波(電流)は、増幅を繰り返す。
\(t=\dfrac{l}{v}\)ごとに増幅するため、以下のような波形になる。
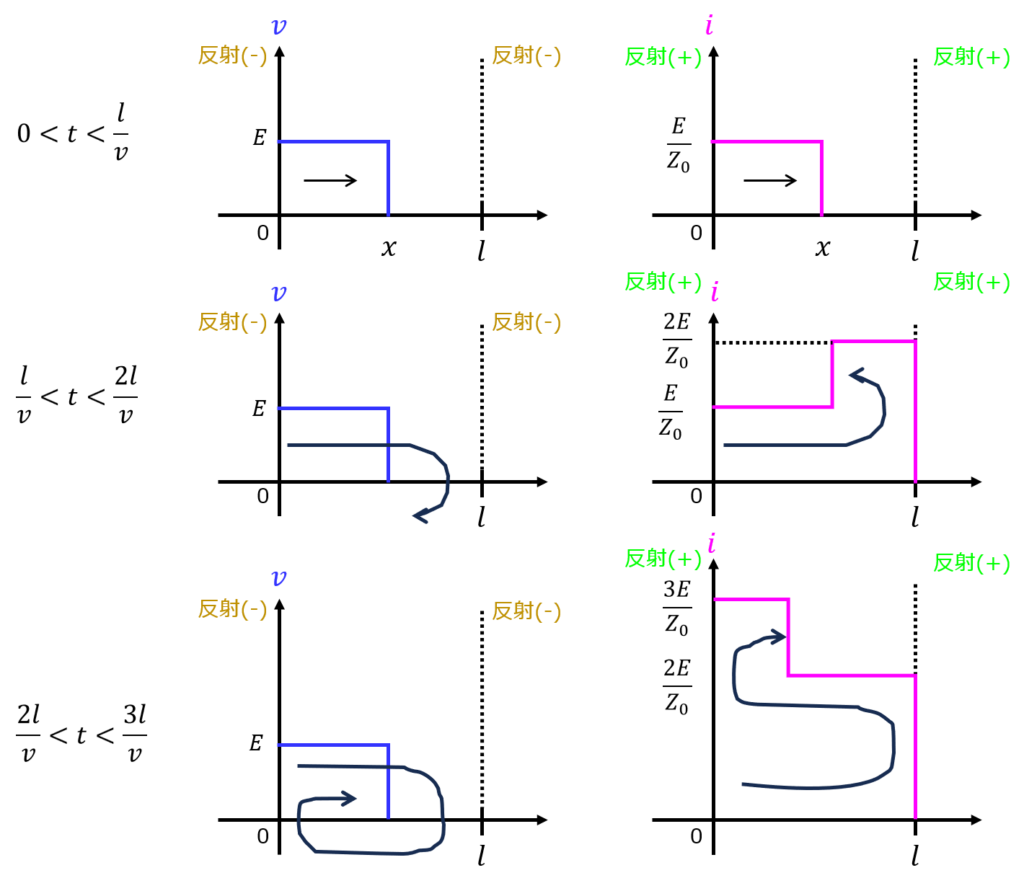
電流が増幅し続け、収束しないことが分かりました。
最後に
分布定数回路の過渡現象を考える問題でオーソドックスなものになります。よって、本問が解けるようになる=汎用性の高い解法を覚えることができます。繰り返し計算することで、是非自身のものにしてください。
参考文献
詳解 電気回路演習(下):大下 眞二郎(著) P304-307