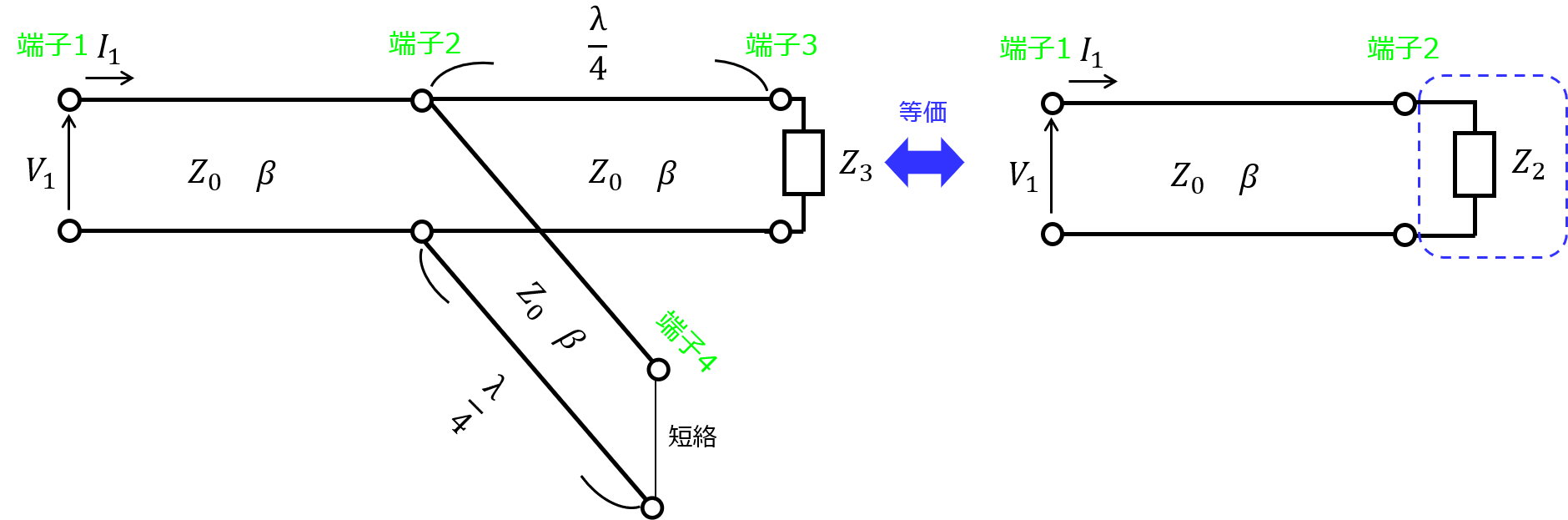
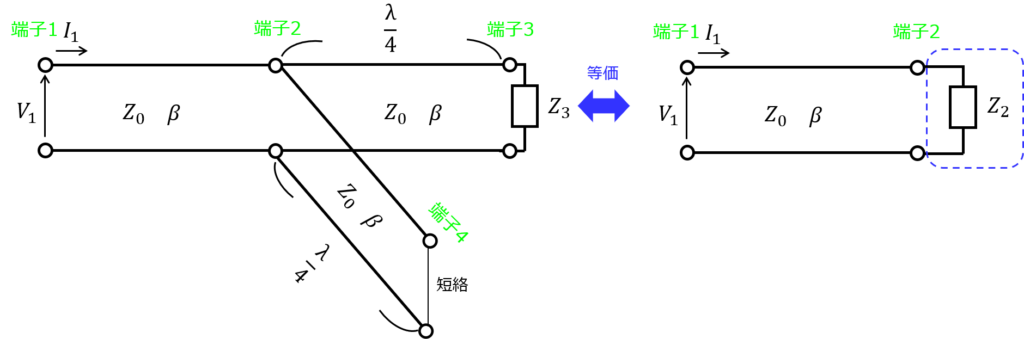
下図(左)のように、端子2から二手に分岐する分布定数回路(無損失)を考える。
これを下図(右)のように\(Z_{2}\)で終端したインピーダンスと等価であると考えると、\(Z_{2}\)はどのような式で表されるか?また、端子2で反射波が発生しないために、\(Z_{3}\)が満たすべき条件は何か。
なお、どの地点でも特性インピーダンスは\(Z_{0}\)とし、端子2-3、端子2-4の距離は\(\frac{\lambda}{4}\)とする。
はじめに
分布定数回路と検索してのアクセスが多いので、さらに類題を紹介します。今回は、並列回路について紹介します。
見た目が仰々しいですが、今までの記事で紹介した考え方を基本として解くことができます。
本記事で覚えてほしいこと
- 端子2から3を見たインピーダンス\(Z_{23}\)、端子2から4を見たインピーダンス\(Z_{24}\)を並列し、端子2におけるインピーダンスを求める。
- 位相定数\(\beta = \frac{2 \pi}{\lambda}\)で表すことができる。
- \(\beta\frac{\lambda}{4}=\frac{\pi}{2}\)により、F行列の\(\cos\)項を削除する。
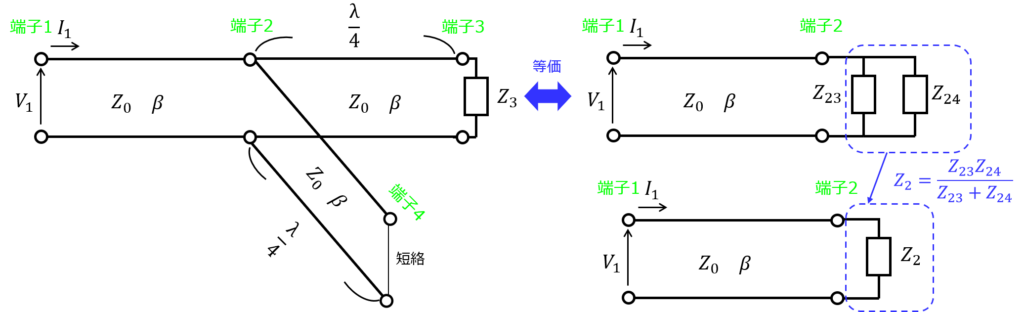
分布定数回路と言えども、基準点からある地点を見た時のインピーダンスは集中定数で表すことができます。このため、端子2から分岐していようとも、分岐先を見たインピーダンスを並列することで、インピーダンス\(Z_{2}\)を表すことが出来ます。
位相定数\(\beta = \frac{2 \pi}{\lambda}\)は、物理学での波数を表しています。これに距離xをかけると位相が分かります。今回は、端子2から3,4への距離は\(\frac{\lambda}{4}\)のため、掛け合わせると\frac{\pi}{2}になります。
以前の記事で紹介したように、無損失分布定数回路のF行列は以下で表されます。
\begin{eqnarray}\begin{pmatrix} \cos \beta x & jZ_{0}\sin \beta x \\ j\dfrac{1}{Z_{0}}\sin \beta x & \cos \beta x \end{pmatrix}\end{eqnarray}
\(\cos \dfrac{\pi }{2}=0,\sin \dfrac{\pi }{2}=1\)のため、F行列は下記のようになります。
\begin{eqnarray}\begin{pmatrix} 0 & jZ_{0} \\ j\dfrac{1}{Z_{0}} & 0 \end{pmatrix}\end{eqnarray}
反射波が発生しない条件は、こちらの記事で説明しています。端子2におけるインピーダンス\(Z_{2}\)が特性インピーダンスに等しいとき、反射係数=0で題意を満たします。
解答例
端子2から3を見たインピーダンス
端子3に流れる電流を\(I_{3}\)、電圧を\(V_{3}\)とする。
前章のF行列の関係から、下記の式で表すことができる。
\begin{eqnarray}\begin{pmatrix} V_{23} \\ I_{23} \end{pmatrix}=\begin{pmatrix} 0 & jZ_{0} \\ j\dfrac{1}{Z} & 0 \end{pmatrix}\begin{pmatrix} V_{3} \\ I_{3} \end{pmatrix}\end{eqnarray}
抵抗\(Z_{3}\)が接続されているので、\(V_{3}=Z_{3}I_{3}\)
\begin{cases}V_{23}=jZ_{0}I_{3}\\ I_{23}=j\dfrac{Z_{3}I_{3}}{Z_{0}}\end{cases}
と連立できるので、\(Z_{23}=\dfrac{V_{23}}{I_{23}}=\dfrac{Z_{0}^{2}}{Z_{3}}\)
端子2から4を見たインピーダンス
端子4は短絡しているので、\(V_{4}=0\)
よって、F行列は以下の式で表される。
\begin{cases}V_{24}=jZ_{0}I_{4}\\ I_{24}=j\dfrac{V_{4}}{Z_{0}}=0\end{cases}
これより、\(Z_{24}=\dfrac{V_{24}}{I_{24}}=\dfrac{jZ_{0}I_{4}}{0}=∞\)
端子2における等価インピーダンス
前節までの経過から、\(Z_{23},Z_{24}\)が求められた。
これを並列することを考える。\(Z_{24}=∞\)の条件に注目し
\begin{eqnarray}Z_{2}=\dfrac{Z_{23}Z_{24}}{Z_{23}+Z_{24}}=Z_{23}=\dfrac{Z_{0}^{2}}{Z_{3}}\end{eqnarray}
であることが分かった。
端子2で反射波が発生しない条件
\(Z_{2}\)が特性インピーダンスと等しければ良いので
\begin{eqnarray}\dfrac{Z_{0}^{2}}{Z_{3}}=Z_{0}\Leftrightarrow Z_{3}=Z_{0}\end{eqnarray}
発展:反射波が発生しないとき、出力端で消費する電力は最大
本問の補足で、以下の回路を考えます。このとき、出力端での消費電力\(P\)を考えます。
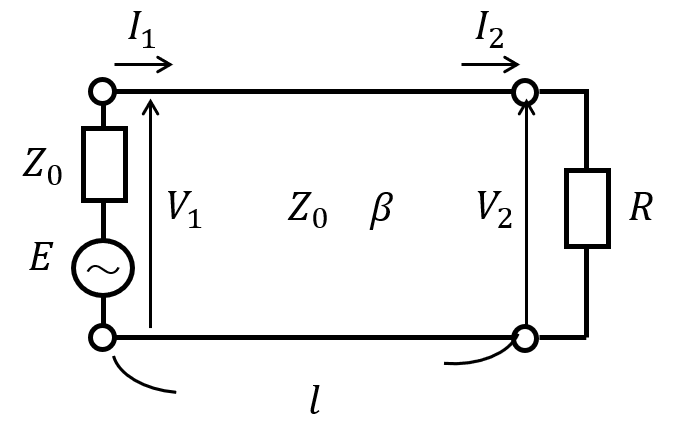
(1)式より
\begin{cases}V_{1}=RI_{2}\cos \beta l+jZ_{0}I_{2}\sin \beta l\\ I_{1}=j\dfrac{RI_{2}}{Z_{0}}\sin \beta l+I_{2}\cos \beta l\end{cases}
\(V_{1}=E-Z_{0}I_{1}\)より、入力電圧と出力電流は下記の関係で整理できる。
\begin{align}E&=\left\{ \left( R+Z_{0}\right) \cos \beta l+j\left( R+Z_{0}\right) \sin \beta l\right\} I_{2} \\ &= I_{2}=\dfrac{E_{0}}{\left( R+Z_{0}\right) \cos \beta l+j\left( R+Z_{0}\right) \sin \beta l}\end{align}
このときの出力端における消費電力は、\(P=R|I_{2}|^{2}\)より
\begin{eqnarray}P=\dfrac{R\left| E\right| ^{2}}{\left( R+Z_{0}\right) ^{2}}\end{eqnarray}
消費電力の最大値は、相加相乗平均の関係より、\(R=Z_{0}\)のとき
\begin{eqnarray}P_{\max }=\dfrac{\left| E\right| ^{2}}{4Z_{0}^{2}}\end{eqnarray}になり、反射波が発生しない条件(インピーダンス整合)と一致します。
物理的には、入力波が全て抵抗で消費される状態を表しており、計算結果とつじつまが合います。
最後に
F行列に対し、回路の条件を代入して最終的に答えを求める方針は、以前の記事から変わりません。暗記がまだの方は、是非とも覚えることを推奨します。