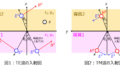
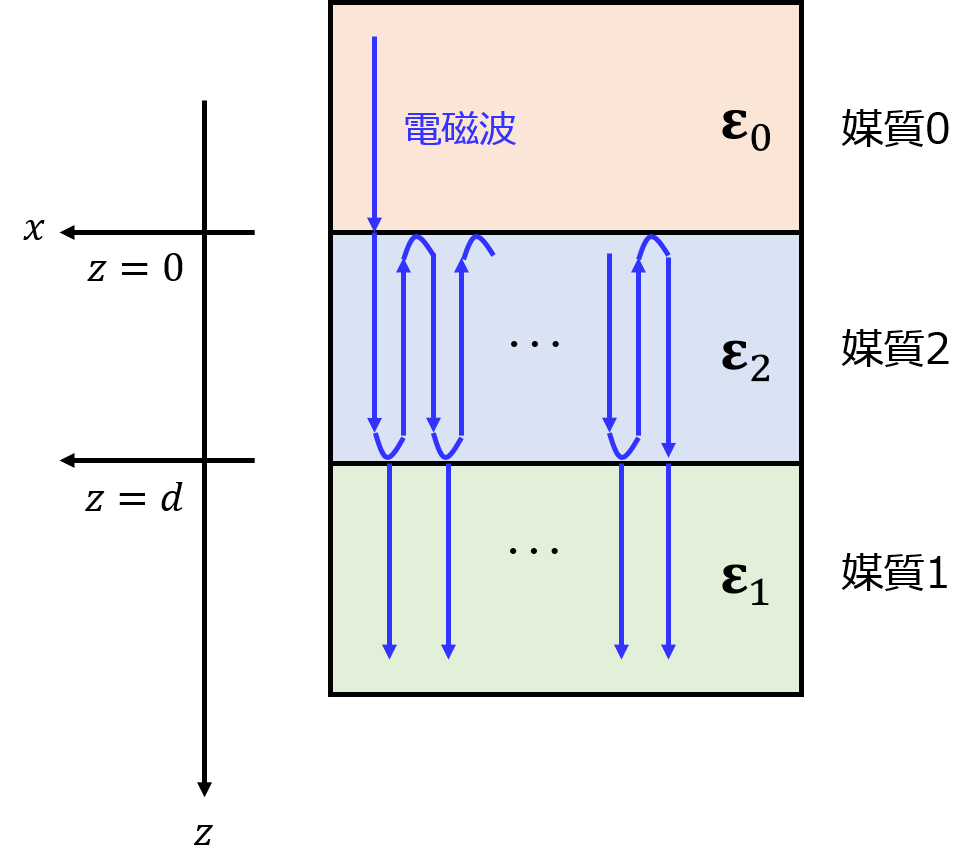
下記のように、誘電体媒質0から2、2から1へ垂直に電磁波を入射する。電場をx方向、磁場をy方向、電磁波の進行方向をzとする。透磁率は共通で\(\mu_{0}\)、誘電率は媒質の添え字番号と対応し、\(\varepsilon_{0},\varepsilon_{1},\varepsilon_{2}\)とする。
(1)まず、誘電体媒質0,2のみを考える。媒質0→2へ電磁波を入射する。媒質2に透過する波の電場\(E_{i2}\)、磁場\(H_{i2}\)媒質0に反射する波の電場\(E_{r0}\)、磁場\(H_{r0}\)を求めよ。
(2)媒質0に反射波が生じない媒質2(厚み\(d\)、誘電率\(\varepsilon_{2}\))の条件を求めよ。但し、\(\varepsilon_{0}≠\varepsilon_{1}\)とする。
はじめに
本問は有名問題です。詳解電磁気学演習でも類題が取り上げられています。
解法の方針として、過去の記事で紹介したように、境界条件を用います。
入射波、反射波、透過波の関係を電場、磁場それぞれ=で結び、式を連立します。
その後、未知数を消去していき、問で求められている式まで計算して答えを求めます。(解答例1)
ただ、実際にやってみると計算が非常に煩雑になります。過去の記事で紹介したブリュースター角の導出以上に時間がかかります。
そこで、本記事では、無限等比級数を用いて解く方法も紹介します。(解答例2)
解答例2では、連立する式が少なく、一本道の計算で求めることができます。管理人としてはこちらをオススメします。是非、これだけでも覗いてみて下さい。
解答例
共通
まず、媒質1から媒質2に電磁波を入力したときの反射係数、透過係数を考えます。
入射波の電場、磁場の振幅を\(E_{i0},H_{i0}\)とすると、電磁波の式は下記で表すことができる。
\begin{aligned}\boldsymbol{E_{i0}}=E_{i0}e^{-jk_{0} z}\boldsymbol{\widehat{x}} \\ \boldsymbol{H_{i0}} = H_{i0} e^{-jk_{0} z}\boldsymbol{\widehat{y}}\end{aligned}
反射波の電場、磁場の振幅を\(E_{r0},H_{r0}\)。媒質2の電場、磁場の振幅を\(E_{i2},H_{i2}\)とすると、\(z=0\)の境界条件より
\begin{cases}E_{i0}+E_{r0}=E_{i2} \\ H_{i0}-H_{r0}=H_{i2}\end{cases}
各媒質中のインピーダンスを\(Z_{0},Z_{1}\)とすると
\begin{aligned}Z_{0}=\dfrac{E_{i0}}{H_{i0}}=\dfrac{E_{r0}}{H_{r0}}=\sqrt{\dfrac{\mu_{0}}{\varepsilon_{0}}},Z_{2}=\dfrac{E_{i2}}{H_{i2}}=\sqrt{\dfrac{\mu_{2}}{\varepsilon_{2}}}\end{aligned}
これを(1)式に代入し、求める反射波は
\begin{aligned}\dfrac{Z_{0}-Z_{2}}{Z_{0}}E_{i0}+\dfrac{Z_{0}+Z_{2}}{Z_{0}}E_{r0}=0 \\ E_{r0}=\dfrac{Z_{2}-Z_{0}}{Z_{2}+Z_{0}}E_{i0}=\dfrac{\sqrt{\varepsilon_{0}}-\sqrt{\varepsilon_{2}}}{\sqrt{\varepsilon_{0}}+\sqrt{\varepsilon_{2}}} \end{aligned}
続いて、透過波は
\begin{aligned}2E_{i0}&=\dfrac{Z_{0}+Z_{2}}{Z_{2}}E_{i2} \\ E_{i2}&=\dfrac{2Z_{2}}{Z_{0}+Z_{2}}E_{i0}\\ &=\dfrac{2\sqrt{\varepsilon_{0}}}{\sqrt{\varepsilon_{0}}+\sqrt{\varepsilon_{2}}}E_{i0}\end{aligned}
\(H_{i2}\)について、\(H_{i2}=\dfrac{E_{i2}}{Z_{2}}=\sqrt{\dfrac{\varepsilon_{2}}{\mu_{2}}}\)より
\begin{aligned}H_{i2}=\sqrt{\dfrac{\varepsilon_{2}}{\mu_{2}}}\dfrac{2\sqrt{\varepsilon_{0}}}{\sqrt{\varepsilon_{0}}+\sqrt{\varepsilon_{2}}}E_{i0}\end{aligned}
解答例1:連立方程式を解く方法
(1)と同様にして、媒質間の電場、磁場の関係を考える。
\(z=0\)に媒質0,2が存在する。境界条件は
\begin{cases}E_{i0}+E_{r0}=E_{i2}+E_{r2} \\ \sqrt{\dfrac{\varepsilon_{0}}{\mu_{0}}}E_{i0}- \sqrt{\dfrac{\varepsilon_{0}}{\mu_{0}}}E_{r0}=\sqrt{\dfrac{\varepsilon_{2}}{\mu_{0}}}E_{i2}+\sqrt{\dfrac{\varepsilon_{2}}{\mu_{0}}}E_{r2}\end{cases}
これを整理して
\begin{aligned}E_{i0}=\dfrac{1}{2}\left(1+\sqrt{\dfrac{\varepsilon_{2}}{\varepsilon_{0}}}\right)E_{i2}+\dfrac{1}{2}\left(1-\sqrt{\dfrac{\varepsilon_{2}}{\varepsilon_{0}}}\right)E_{r2} \\ E_{r0}=\dfrac{1}{2}\left(1-\sqrt{\dfrac{\varepsilon_{2}}{\varepsilon_{0}}}\right)E_{i2}+\dfrac{1}{2}\left(1+\sqrt{\dfrac{\varepsilon_{2}}{\varepsilon_{0}}}\right)E_{r2} \end{aligned}
次に、\(z=d\)での媒質1,2間の境界条件は
\begin{cases}E_{i2}e^{-jk_{2}d}+E_{r2}e^{jk_{2}d}=E_{i1}e^{-jk_{1}d} \\ \sqrt{\dfrac{\varepsilon_{2}}{\mu_{0}}}E_{i2}e^{-jk_{2}d}-\sqrt{\dfrac{\varepsilon_{2}}{\mu_{0}}}E_{r2}e^{jk_{2}d}=\sqrt{\dfrac{\varepsilon_{1}}{\mu_{0}}}E_{i1}e^{-jk_{1}d} \end{cases}
(1)と同じようにして
\begin{aligned}E_{i2}=\dfrac{1}{2}\left(1+\sqrt{\dfrac{\varepsilon_{1}}{\varepsilon_{2}}}\right)E_{i1}e^{-j(k_{1}-k_{2})d} \\ E_{r2}=\dfrac{1}{2}\left(1-\sqrt{\dfrac{\varepsilon_{1}}{\varepsilon_{2}}}\right)E_{i1}e^{-j(k_{1}+k_{2})d}\end{aligned}
を得る。
(8)に(10)を代入すると
\begin{align}E_{i0}=\dfrac{1}{4} \left( \left( 1+\sqrt{\dfrac{\varepsilon_{2}}{\varepsilon _{0}}} \right) \left( 1+\sqrt{\dfrac{\varepsilon_{1}}{\varepsilon_{2}}}\right) e^{jk_{2}d}+\left( 1-\sqrt{\dfrac{\varepsilon_{2}}{\varepsilon_{0}}} \right) \left( 1-\sqrt{\dfrac{\varepsilon_{1}}{\varepsilon_{2}}} \right) e^{-jk_{2}d} \right) e^{-jk_{1}d} E_{i1} \\ E_{r0}=\dfrac{1}{4} \left( \left( 1-\sqrt{\dfrac{\varepsilon_{2}}{\varepsilon _{0}}} \right) \left( 1+\sqrt{\dfrac{\varepsilon_{0}}{\varepsilon_{2}}}\right) e^{jk_{2}d}+\left( 1+\sqrt{\dfrac{\varepsilon_{2}}{\varepsilon_{0}}} \right) \left( 1-\sqrt{\dfrac{\varepsilon_{1}}{\varepsilon_{2}}} \right) e^{-jk_{2}d} \right) e^{-jk_{1}d} E_{i1} \end{align}
を得る。
(11)を変形し
\begin{aligned}E_{i1}=\dfrac{4e^{jk_{1}d}}{\left( \left( 1+\sqrt{\dfrac{\varepsilon_{2}}{\varepsilon _{0}}} \right) \left( 1+\sqrt{\dfrac{\varepsilon_{1}}{\varepsilon_{2}}}\right) e^{jk_{2}d}+\left( 1-\sqrt{\dfrac{\varepsilon_{2}}{\varepsilon_{0}}} \right) \left( 1-\sqrt{\dfrac{\varepsilon_{1}}{\varepsilon_{2}}} \right) e^{-jk_{2}d} \right)}E_{i0} \end{aligned}
\begin{align}H_{i1}=\sqrt{\dfrac{\varepsilon_{1}}{\mu_{0}}}\dfrac{4e^{jk_{1}d}}{\left( \left( 1+\sqrt{\dfrac{\varepsilon_{2}}{\varepsilon _{0}}} \right) \left( 1+\sqrt{\dfrac{\varepsilon_{1}}{\varepsilon_{2}}}\right) e^{jk_{2}d}+\left( 1-\sqrt{\dfrac{\varepsilon_{2}}{\varepsilon_{0}}} \right) \left( 1-\sqrt{\dfrac{\varepsilon_{1}}{\varepsilon_{2}}} \right) e^{-jk_{2}d} \right)}E_{i0}\end{align}
(12)に(13),(14)をそれぞれ代入し、求める反射波(電場、磁場)は下記になる。
\begin{aligned}E_{r0}=\dfrac{\left( \left( 1-\sqrt{\dfrac{\varepsilon_{2}}{\varepsilon _{0}}} \right) \left( 1+\sqrt{\dfrac{\varepsilon_{1}}{\varepsilon_{2}}}\right) e^{jk_{2}d}+\left( 1+\sqrt{\dfrac{\varepsilon_{2}}{\varepsilon_{0}}} \right) \left( 1-\sqrt{\dfrac{\varepsilon_{1}}{\varepsilon_{2}}} \right) e^{-jk_{2}d} \right)}{{\left( \left( 1+\sqrt{\dfrac{\varepsilon_{2}}{\varepsilon _{0}}} \right) \left( 1+\sqrt{\dfrac{\varepsilon_{1}}{\varepsilon_{2}}}\right) e^{jk_{2}d}+\left( 1-\sqrt{\dfrac{\varepsilon_{2}}{\varepsilon_{0}}} \right) \left( 1-\sqrt{\dfrac{\varepsilon_{1}}{\varepsilon_{2}}} \right) e^{-jk_{2}d} \right)}}E_{i0}\end{aligned}
\begin{aligned}H_{r0}=\sqrt{\dfrac{\varepsilon_{0}}{\mu_{0}}}E_{r0}\end{aligned}
反射波が0になるとき、(15)式の分子が0になれば良いので
\begin{aligned} \left( 1-\sqrt{\dfrac{\varepsilon_{2}}{\varepsilon _{0}}} \right) \left( 1+\sqrt{\dfrac{\varepsilon_{1}}{\varepsilon_{2}}}\right) e^{jk_{2}d}=±\left( 1+\sqrt{\dfrac{\varepsilon_{2}}{\varepsilon_{0}}} \right) \left( 1-\sqrt{\dfrac{\varepsilon_{1}}{\varepsilon_{2}}} \right) e^{-jk_{2}d} \end{aligned}
を考える。
(i)右辺が+のとき、\(e^{-jk_{2}d}=-j\)なので、\(k_{2}d=(n+\frac{1}{2})\pi\)
このとき、\begin{aligned}2\sqrt{\dfrac{\varepsilon_{1}}{\varepsilon_{2}}}=2\sqrt{\dfrac{\varepsilon_{2}}{\varepsilon_{0}}}\end{aligned}
で、これを解くと\(\varepsilon_{2}=\sqrt{\varepsilon_{0}\varepsilon_{1}}\)
問題の条件と反さないので、適する。
(ii)右辺が-のとき、\(e^{-jk_{2}d}=1\)なので、\(k_{2}d=n\pi\)
\begin{aligned}1+\sqrt{\dfrac{\varepsilon_{1}}{\varepsilon_{2}}}-\sqrt{\dfrac{\varepsilon_{2}}{\varepsilon_{0}}}-\sqrt{\dfrac{\varepsilon_{1}}{\varepsilon_{0}}}=-1+\sqrt{\dfrac{\varepsilon_{1}}{\varepsilon_{2}}}-\sqrt{\dfrac{\varepsilon_{2}}{\varepsilon_{0}}}+\sqrt{\dfrac{\varepsilon_{1}}{\varepsilon_{0}}}\end{aligned}
\(2=2\sqrt{\dfrac{\varepsilon_{1}}{\varepsilon_{0}}}\)より、\(\varepsilon_{0}=\varepsilon_{1}\)が得られるが、問題の条件と反するので不適。
結論
前節より、反射波が発生しない条件は
\begin{cases}d=\dfrac{2n+1}{2k_{2}}π \\ \varepsilon_{2}=\sqrt{\varepsilon_{0}\varepsilon_{1}}\end{cases}
・・・途中計算をなるべく端折って書きましたが、それでもこれだけの計算をしなければなりません。
読者の方も、読んでいて疲れたのではないでしょうか。
符号の関係も気を付けなければならず、一つでも間違えてしまうと正しい答えにはたどり着けません。
計算が難しくなる理由の一つに、長い連立方程式をひたすら解き続ける必要があります。
次に紹介する方法2では、これをスキップすることができます。
解答例2:無限等比級数を用いた解法
(1)の結果より、各媒質間の反射率、透過率を考える。
媒質0から2に対する反射率を\(r_{0}\)、透過率を\(t_{0}\)とすると
\begin{cases}r_{0}=\dfrac{n_{0}-n_{2}}{n_{0}+n_{2}} \\ t_{0}=\dfrac{2n_{0}}{n_{0}+n_{2}}\end{cases}
ただし、\(n_{0},n_{1},n_{2}\)は媒質中の屈折率です。
真空中での光速\(c\)と、その媒質中での光速\(v\)の比を考えて、下記で表すことができます。
\begin{cases}n_{0}=\dfrac{v_{0}}{c}=\sqrt{\dfrac{\varepsilon_{0}\mu_{0}}{\varepsilon_{0}\mu_{0}}}=1 \\ n_{1}=\dfrac{v_{1}}{c}=\sqrt{\dfrac{\varepsilon_{0}\mu_{0}}{\varepsilon_{1}\mu_{0}}}=\sqrt{\dfrac{\varepsilon_{0}}{\varepsilon_{1}}} \\ n_{2}=\dfrac{v_{2}}{c}=\sqrt{\dfrac{\varepsilon_{0}\mu_{0}}{\varepsilon_{2}\mu_{0}}}=\sqrt{\dfrac{\varepsilon_{0}}{\varepsilon_{2}}}\end{cases}
媒質2から0に対する反射率を\(r_{1}\)、透過率を\(t_{1}\)とすると、(21)式の\(n_{0},n_{2}\)を入れ替えれば良いので
\begin{cases}r_{1}=\dfrac{n_{2}-n_{0}}{n_{0}+n_{2}} \\ t_{1}=\dfrac{2n_{2}}{n_{0}+n_{2}}\end{cases}
媒質2から1に対する反射率を\(r_{2}\)、透過率を\(t_{2}\)とすると、
\begin{cases} r_{2}= \dfrac{n_{2}-n_{1}}{n_{1}+n_{2}} \\ t_{2}=\dfrac{2n_{2}}{n_{1}+n_{2}}\end{cases}
媒質0に生じる反射波の電場成分\(E_{r0}\)を求める。
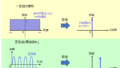
媒質0→2に入射したとき、直接反射する波
媒質0→2へ一度透過してから媒質1の界面で一度反射し、媒質2→0へ透過し戻ってくる波
二度反射する場合、三度反射する場合、、、n度反射してから媒質2→0へ透過する波の重ね合わせである。
これを級数として表すと
\begin{aligned}E_{r0}=E_{i0}r_{0}+E_{i0}t_{0}r_{2}t_{1}e^{j2k_{2}d}+E_{i0}t_{0}r_{2}r_{1}r_{2}t_{1}e^{j4k_{2}d}+\cdots +E_{i0}t_{0}(r_{2}r_{1})^{n-1}r_{2}t_{1}e^{j2nk_{2}d} \end{aligned}
公比\(r_{1}r_{2}e^{2k_{2}d}\)の数列として考えられるので、\(n→∞\)の極限を考えると
\begin{aligned}E_{r0}&=E_{i0}r_{0}+\dfrac{t_{0}t_{1}r_{2}e^{j2k_{2}d}}{1-r_{1}r_{2}e^{2k_{2}d}}E_{i0} \\ &=\dfrac{r_{0}-r_{1}r_{2}r_{0}e^{j2k_{2}d}+t_{0}t_{1}r_{2}e^{j2k_{2}d}}{1-r_{1}r_{2}e^{2k_{2}d}}E_{i0} \end{aligned}
反射波が生じないためには、(26)式の分子が0になれば良い
実部も虚部も0になる必要があり、オイラーの公式より
\begin{aligned}e^{2k_{2}d}=\cos(2k_{2}d)+j\sin(2k_{2}d)\end{aligned}だから
\begin{cases}\sin(2k_{2}d)=0 \\ \cos(2k_{2}d)=-1\end{cases}
を同時に満たせば良い。(\(\cos(2k_{2}d)=1\) の場合は、分子が0より大きくなるので不適)
これを実現するには、\(2k_{2}d=(2n+1)\pi\)を満たせば良い。
このとき、(26)式は、
\begin{aligned}E_{r0}=\dfrac{r_{0}+r_{2}(r_{0}r_{1}-t_{0}t_{1})}{1-r_{1}r_{2}e^{2k_{2}d}}\end{aligned}
\begin{aligned}r_{0}r_{1}-t_{0}t_{1}=\dfrac{n_{0}-n_{2}}{n_{0}+n_{2}}\dfrac{n_{2}-n_{0}}{n_{0}+n_{2}}-\dfrac{2n_{0}}{n_{0}+n_{2}}\dfrac{2n_{2}}{n_{0}+n_{2}}=-1\end{aligned}
なので、
\begin{aligned}E_{r0}=(r_{0}-r_{2})E_{i0}\end{aligned}
反射波が生じない時、\(r_{0}-r_{2}\)であれば良いので
\begin{aligned}\dfrac{n_{0}-n_{2}}{n_{0}+n_{2}}-\dfrac{n_{2}-n_{1}}{n_{1}+n_{2}}=0 \end{aligned}
これを簡単にして
\begin{aligned} n^{2}_{2}=n_{0}n_{1}\end{aligned}
\begin{aligned}\dfrac{\varepsilon_{0}}{\varepsilon_{2}}=\sqrt{\dfrac{\varepsilon_{0}}{\varepsilon_{1}}}\end{aligned}
\begin{aligned}\varepsilon_{2}=\sqrt{\varepsilon_{0}\varepsilon_{1}}\end{aligned}
を得る。
いかがでしょうか。解答例1のように、長い式変形が無いことが分かります。
等比級数の合計値が0になれば良いという発想を用いることで、楽に解くことができました。
限りある試験時間です。万が一本問が出題された際は、解答例2で解くことができるよう、日ごろから訓練することをオススメします。
参考文献
詳解電磁気学演習 P334