はじめに
本記事では、半導体デバイスの序盤で勉強するフェルミディラックの分布関数の説明と、電子密度の導出方法についてまとめていきます。
実を言うと、本内容は院試で何かと出題されます。頻出分野のMOSFET、PN接合トランジスタばかりの勉強だと足元をすくわれることがあります。そんなことが無いように、本記事では院試の頻出事項を中心にまとめていきます。
フェルミ・ディラックの分布関数とは
電子のエネルギー準位ごとの存在確率を表します。エネルギー\(E\)を変数とした記号\(F(E)\)を用いて下記の式で表されることが多いです。(\(k\)はボルツマン定数、\(T\)は温度、\(E_{F}\)はフェルミエネルギー)
\begin{aligned}F(E)=\dfrac{1}{1+\exp\left(\dfrac{E-E_{F}}{kT}\right)}\end{aligned}
他記事でも頻繁に使用していますが、半導体の特性解析を行う上で不可欠な分布関数になります。理由は、金属(またはそれに近い性質を持つ物質)中の電子の振る舞いを最も忠実に表しているからです。
マクスウェル-ボルツマン分布関数の場合
| 分布関数 | 粒子 | パウリの排他原理 | 使用用途 |
| フェルミ・ディラック | フェルミ粒子(電子) | 適用可能 | 半導体解析 |
| マクスウェル・ボルツマン | 古典粒子 | 無視 | 気体 |
| ボーズ・アインシュタイン | ボーズ粒子(光子、フォノン) | 適用不可 | レーザー |
フェルミ・ディラックの分布関数以外に使用される分布関数のうち、最も代表的なものになります。標記の分布関数は、下記のように表されます。
\begin{aligned}F(E)=\exp\left(\dfrac{E}{kT}\right)\end{aligned}
マクスウェル-ボルツマン分布関数は、気体分子の密度を考えるために使用されることが多いです。気体分子密度のオーダーは10^25m^-3に対し、金属中の電子密度は10^28~29m^-3あります。対象とするオーダーが違うため、ボルツマン分布を使用すると誤差が大きくなってしまいます。
また、電子はパウリの排他原理に従い、一つの準位に存在する電子は共通の量子状態を持てない性質があります。マクスウェル-ボルツマン分布は古典粒子を対象としており、パウリの排他原理は適用できないため、ここでも正確に評価ができなくなります。
同じことがボーズ・アインシュタイン分布にも言えます。一方で、フェルミ・ディラックの分布関数の場合、ここで紹介したデメリットは起こらないので、使用することは適切だと考えられます。
分布関数の比較
前章で述べた3つの分布関数を、横軸をエネルギーとして実際にプロットしてみましょう。(温度は、常温の想定)
結論、下記のようになります。高エネルギー帯ではどれも似たり寄ったりですが、低エネルギー帯になるにつれ、フェルミ・ディラックの分布関数のみ1を示すことが分かります。他の分布関数は発散しており、フェルミ・ディラックの分布関数が最も高精度なことが分かりました。

絶対零度下でのフェルミ・ディラック分布関数
絶対零度下では、(1)式exp項の分母が∞になります。よって、分子の正負によりexp項が0になるか発散するか決まります。
- 0の場合(\(E<E_{F}\))は、\(F(E)=1\)となり、存在確率が1
- 発散する場合(\(E>E_{F}\))は、\(F(E)=0\)となり、存在確率が0
となり、\(E_{F}\)次第で\(F(E)\)の値が離散的に変わります。ステップ状の振る舞いをすることから、下記のグラフになります。同様にテストで出てくるので覚えておきましょう。

状態密度と電子密度
あるエネルギー準位における電子密度\(n(E)\)は、状態密度\(g(E)\)とフェルミ・ディラックの分布関数\(F(E)\)の積で表されます。
\begin{aligned}n(E)=g(E)F(E)\end{aligned}
状態密度\(g(E)\)とは
あるエネルギーに存在できる量子状態の数を言います。前述した通り、電子はパウリの排他原理に従うことから、離散的なエネルギー状態を取ります。単位長さの立方体を考える場合、エネルギー状態は下記のようになります。
\begin{aligned}E_{n}=\dfrac{1}{2m}\left(\dfrac{h}{2}\right)^{2}\cdot(n_{x}^{2}+n_{y}^{2}+n_{z}^{2})\end{aligned}
\(r=\sqrt{n_{x}^{2}+n_{y}^{2}+n_{z}^{2}}\)であり、スピン状態としては↑↓の2種類存在するため、エネルギーが0からEまでの間にある状態の総数を\(N(E)\)とすると
\begin{aligned}N(E)&=2\cdot\dfrac{1}{8}\cdot \dfrac{4}{3}\pi r^{3} \\ &=\dfrac{\pi}{3}\left(2m\left(\dfrac{2}{h}\right)^{2}\cdot E\right)^{\frac{3}{2}}\end{aligned}
上式をエネルギーで微分すると、あるエネルギー準位Eから+dEの領域における状態数\(g(E)\)が出てくるので
\begin{aligned}g(E)=\dfrac{\pi}{2}\left(2m\left(\dfrac{2}{h}\right)^{2} \right)^{\frac{3}{2}}E^{\frac{1}{2}}\end{aligned}
エネルギー\(E\)の1/2乗に比例することから、エネルギーが多くなるほど収容可能な状態数が増えることが分かりました。
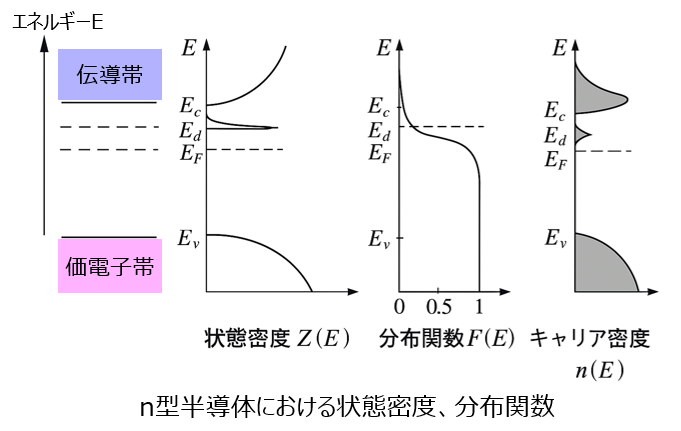
参考:n型半導体の各種関数
n型半導体は、価電子数が5の不純物(P:リンなど)をシリコン中にドープしたものになります。フェルミ準位は伝導帯寄りに存在(ドナー準位)し、状態密度\(Z(E)\)、分布関数\(F(E)\)、キャリア密度\(n(E)\)は下記のようになります。

※\(E_{d}\)はドナー準位です。
最後に
本記事の内容は、実際に東大の院試で出題されたことがあります。最高学府の院試でも問われることがありますので、他の大学の院試を受ける方も是非覚えましょう。
また、