npnバイポーラトランジスタの動作原理をバンド図を使用して説明せよ。
また、特性を向上させるための施策、制約について述べよ。
はじめに
npnバイポーラトランジスタに関する問題は、論述形式で出題されることが多いです。本記事も、論述ベースで作成していきます。
よって、覚えてほしいことは解答例の内容全てになります。
解答例
npnバイポーラトランジスタの構造
下記のように、エミッタ、ベース、コレクタで構成されます。
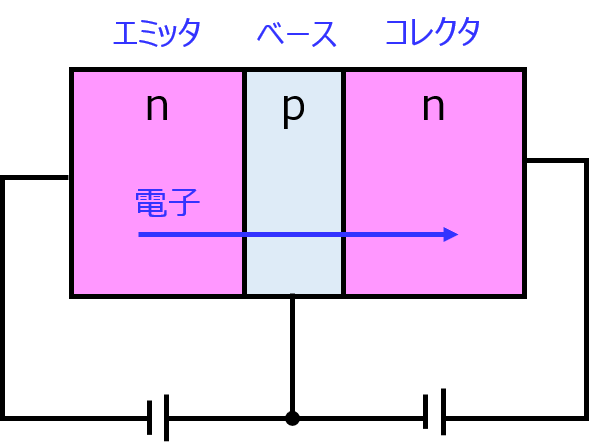
エミッタは、電子を放出する場所。ベースは電子の放出を制御する場所。コレクタは電子を受け取る場所です。
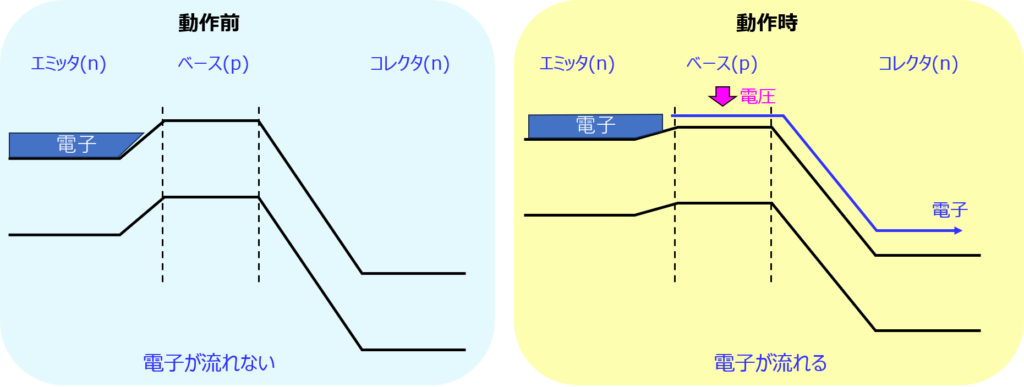
バンド図では、上記のように表されます。ベースに電圧をかけていない状態では、ベースがエネルギー障壁になり、コレクタへ電子が流れません。
そこで、ベースに順方向電圧をかけます。すると、エミッタからベースを介し、コレクタへ電子が流れる構造になっています。
ベース幅は狭いため、コレクタと正孔はあまり結合せず、損失少なくコレクタへ電子を流すことができます。
特性向上のための施策
特性向上=コレクタへ電子が流れる量が増える。という考え方で説明していきます。
- そもそもの流れる電子の量を上げる
- ベースでの再結合確率を下げる
以上2点を考えると良いので、以下の施策が考えられます。
- エミッタの不純物電子濃度を上げる
- ベース幅を狭くし、再結合確率を低減する
確かに、理屈で言えば上記1.2.で達成できそうです。しかし、際限なく特性向上できるのでしょうか。次節では、特性向上を考える際の制約について紹介していきます。
制約について
前節の説明から、BPPの特性が向上するほど、大電流が流れ、印加する電圧も大きくなります。そうなると、今まで無視できた要素が無視できなくなります。本節では、4つ説明していきます。
エミッタ,ベース,コレクタ抵抗による特性の変化
前節までの説明では、エミッタ,ベース,コレクタの抵抗は無視していました。
しかし、実際にはそれぞれの部位に内部抵抗(拡散層抵抗)を持ち、エミッタ-ベース間、ベース-コレクタ間には接触抵抗が存在します。
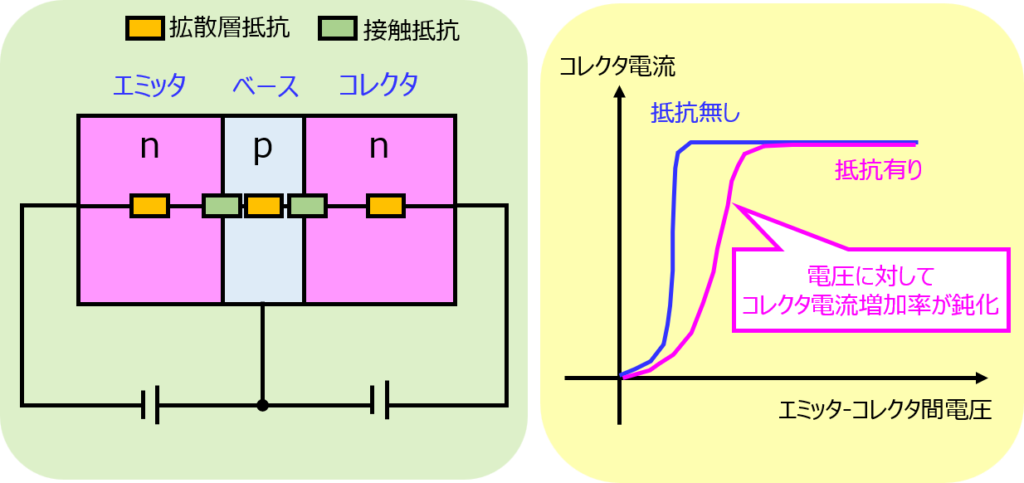
電流が小さいときは、電圧降下が小さかったため影響を無視できましたが、大電流になるにつれて無視できなくなります。
ですので、理論値通りに電流が流れない事象が発生します。
アーリー効果(ベース幅変調効果)
コレクタ電圧を大きくしたときに発生する現象です。
ベース-コレクタ間のバンドギャップが大きくなり、空乏層幅が大きくなった結果ベース幅が狭くなります。
これだけ考えると、「電子と正孔の再結合確率が低下するので、特性向上に寄与するのでは?」と考えるかもしれません。しかし、それよりも大きな問題があります。
本来、ベース電圧によって制御すべきトランジスタが正常動作しなくなります。コレクタ電流で動作するようになると、誤動作の原因になり、思った通りの特性が出なくなります。
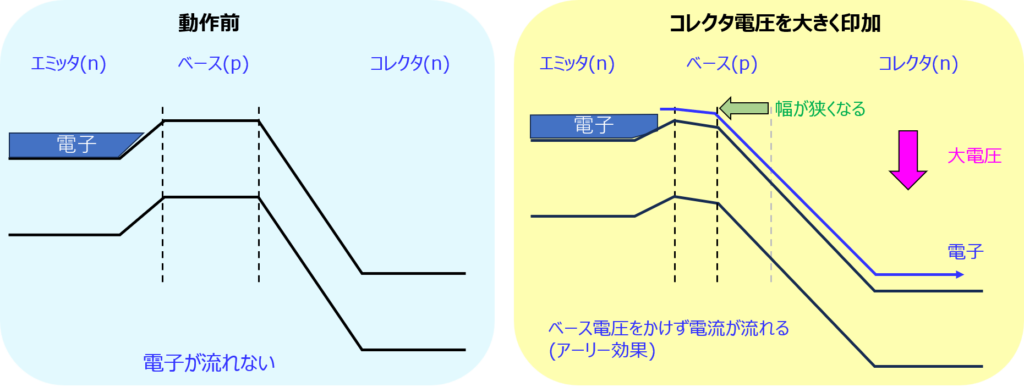
対策として、コレクタの不純物濃度は、ベースよりも小さくし、空乏層をなるべく発生させない方法があります。
高水準濃度の電子をベースに注入したときの制約
今度は、エミッタ-ベース間の電圧を大きくした場合です。
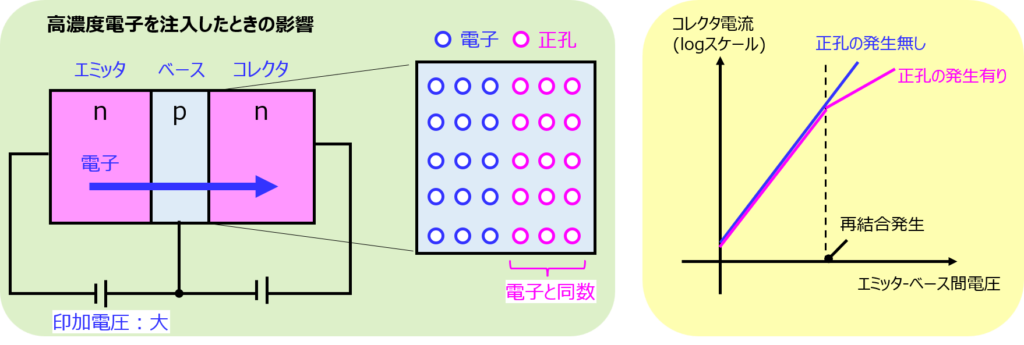
印加電圧を大きくするほど、エミッタ⇒ベースへ流れる電流値が大きくなります。しかし、ベースの不純物濃度以上にエミッタから電子を流した際に出てくる影響があります。
電気的に中性になるように、注入された電子と同じ数の正孔がベースから出てくるようになり、再結合確率が上昇します。
その結果、コレクタ電流の上昇が鈍化し、印可した電圧ほどの効果が出てこなくなります。
アバランジェ破壊
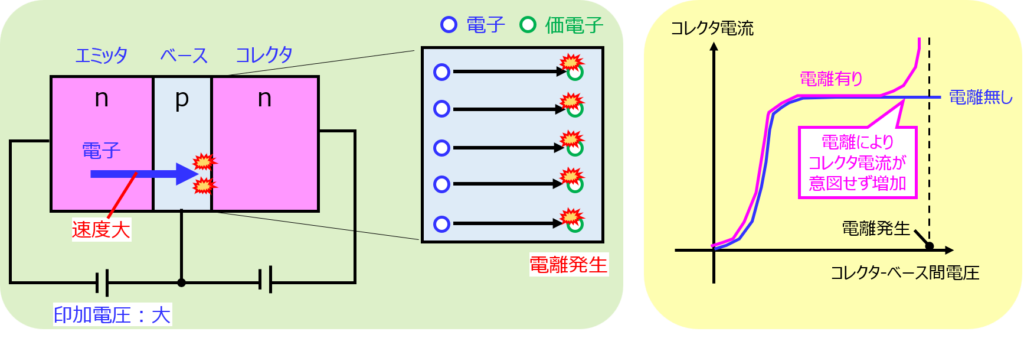
印加電圧を大きくすると、エミッタからベースに流れる電子の速度が大きくなります。よって、電子の持つエネルギーが多くなります。
このときに、ベースの価電子と衝突した際に発生する現象です。バンドギャップ以上のエネルギーを持つ状態で衝突すると、電離が発生します。
これが繰り返されることで、非常に大きなコレクタ電流が流れます。結果、非常に大きなジュール熱が発生し、素子の破壊に繋がる可能性があります。
電離に関しては、下記記事でも説明しています。
増幅の3条件
前節まではトランジスタ単体での増幅を考えてきました。
最後に、電気回路としてみた時の増幅条件を考えます。
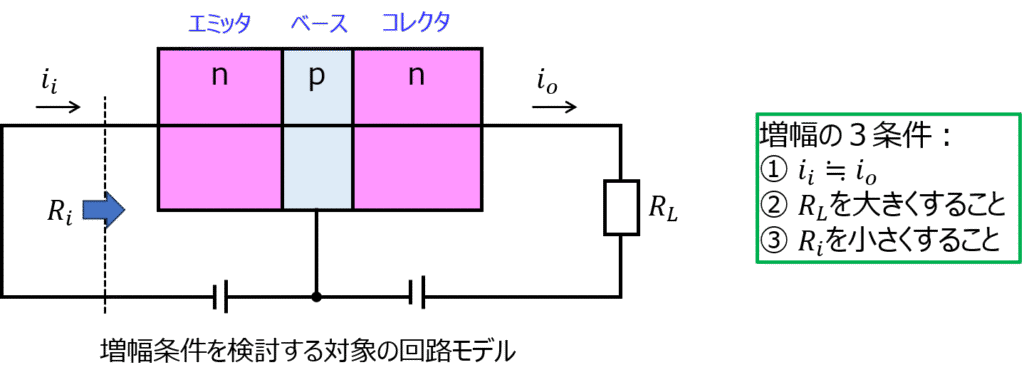
- 入力電流と出力電流がなるべく等しいこと
- 出力抵抗をなるべく大きくすること
- 入力抵抗をなるべく小さくすること
理由を見ていきましょう。
与えられたパラメータより、入力電力\(P_{i}\)と出力電力\(P_{o}\)は
\begin{aligned}P_{i}=R_{i}i_{i}^{2} \\ P_{o}=R_{L}i_{o}^{2}\end{aligned}
よって、この場合の電力利得\(G\)は
\begin{aligned}G=\dfrac{P_{o}}{P_{i}}=\dfrac{R_{i}i_{i}^{2}}{R_{L}i_{o}^{2}}\end{aligned}
入力電流があまり減衰せずに出力電流と等しくなるとき、\(i_{i}=i_{o}\)であり
\begin{aligned}G=\dfrac{R_{L}}{R_{i}}\end{aligned}
になります。
よって、出力抵抗\(R_{L}\)が大きく、入力抵抗\(R_{i}\)が小さくなるほど、利得\(G\)が大きくなることが分かります。
増幅の3条件:①入力電流と出力電流を等しくするための方策
前節で述べたように、ベース幅を狭くすると良いです。
電子の再結合確率が小さくなるので入力電流が減衰することなく出力端までたどり着きます。
ただし、アーリー効果には注意しましょう。
増幅の3条件:②出力抵抗を大きくするための方策
ベース-コレクタ間の抵抗値を大きくすると良いです。
よって、ベース-コレクタ間の逆バイアス電圧を大きくするほど空乏層が大きくなり、接合抵抗(容量)が大きくなります。
増幅の3条件:③入力抵抗を小さくするための方策
方策②と逆の操作をすればよいです。
エミッタ-ベース間の順バイアス電圧をかけて、なるべく空乏層を小さくします。
まとめ
増幅の3条件は、トランジスタがnpnでもpnpでもやることは変わりません。
ベース-コレクタ間は逆バイアス。エミッタ-ベース間は順バイアス電圧をかけることがポイントです。
最後に
半導体デバイスの院試問題では、論述が出題されることがよくあります。MOSトランジスタの動作については、下記の記事で詳しく紹介しています。
参考文献
半導体デバイス 絵から学ぶ:谷口 研二(著) 宇野 重康(著)第4章
半導体デバイス(series電気・電子・情報系):松波 弘之(著) P107-111