例題を用いたグラムシュミットの直交化法の解説

数学

2024.03.142024.12.06

問題

3次元実ベクトル空間の元 $a = (\begin{matrix} 2 \\ 0 \\ 0 \end{matrix}), b = (\begin{matrix} 0 \\ - 1 \\ 0 \end{matrix}), c = (\begin{matrix} 1 \\ 1 \\ 1 \end{matrix})$ を考える。
3つのベクトルは全て線形独立であり、 $a と b$ は互いに直交している。 $a 、 b$ を基底の一部とし、正規直交基底を作成せよ。

グラムシュミットの直交化とは
本記事で覚えたいこと
解答例
最後に
参考文献

グラムシュミットの直交化とは

あるベクトル群を直交座標に変換する手法です。

これにより、複雑な関数を人間が理解しやすい形に変換することができます。

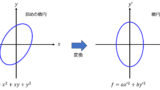
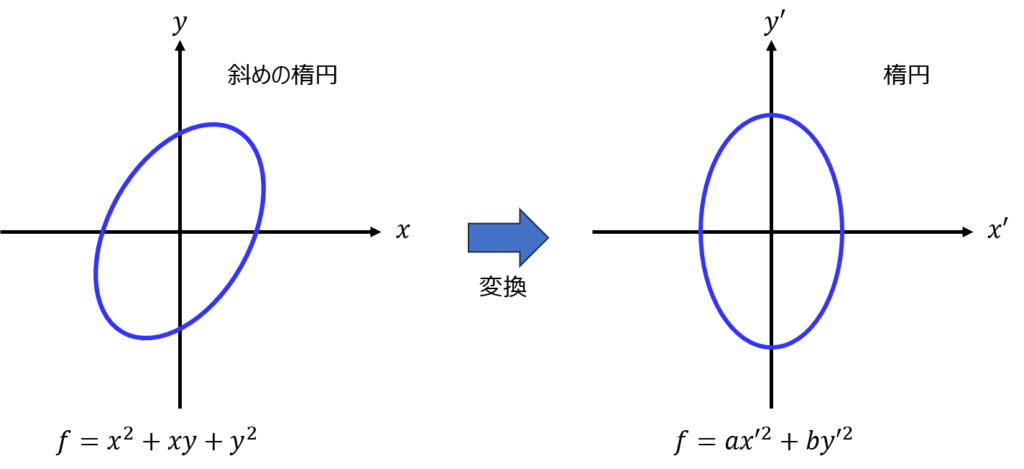
例えば、xy項が含まれている2次形式の関数を座標変換し、x,yそれぞれの式の楕円体で表すことができます。

本記事で覚えたいこと

正規直交化の手順

既に直交しているベクトルを単位ベクトル $u_{1}, u_{2} \dots$ に変換する
グラムシュミットの直交化法により、新たに直交ベクトル $v_{3}$ を以下の式で求める
$v_{3} = c - (u_{1} ･ c) ･ u_{1} - (u_{2} ･ c) ･ u_{2} \dots$
$v_{3}$ を単位ベクトルにする

補足

グラムシュミットの直交化法を平易な言語として置き換えると以上のようになりました。
式の意味は他サイト様の解説が充実しています。

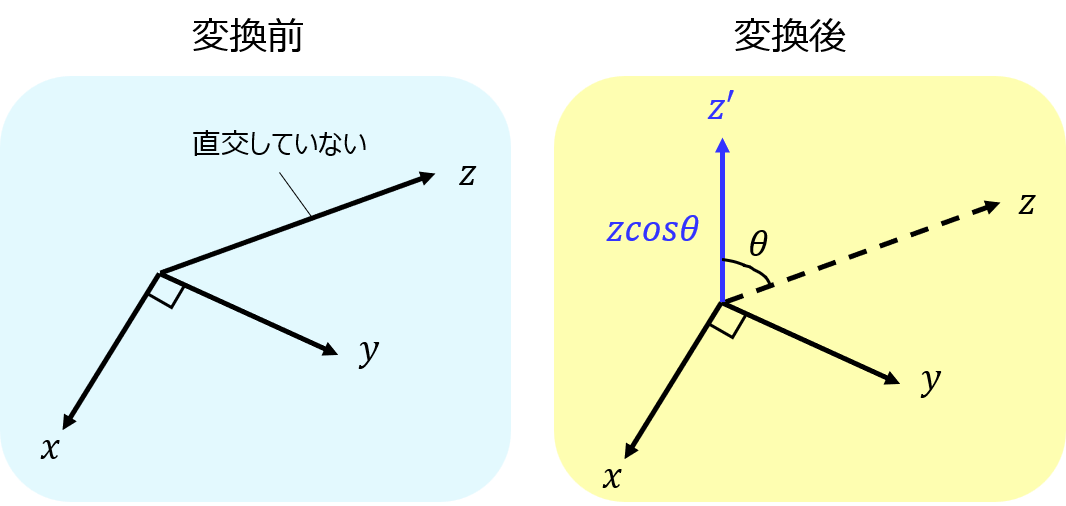
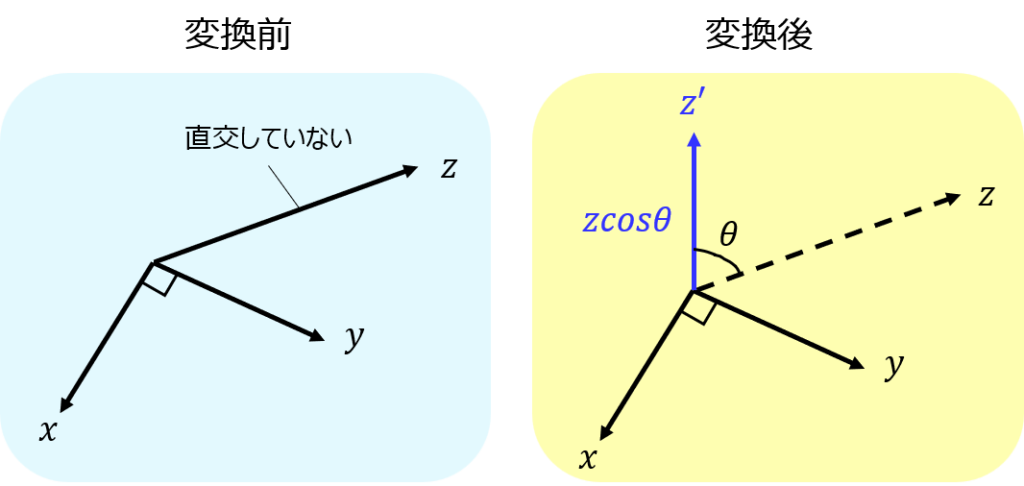
一言で申し上げると、下図のようになります。正規直交基底に変換対象のベクトル $c$ を、自身の正射影と引くと、直交ベクトルになります。

解答例

まず、 $a$ , $b$ を単位ベクトル $u_{1}, u_{2}$ に変換する。

$u_{1} = \frac{1}{2} (\begin{matrix} 2 \\ 0 \\ 0 \end{matrix}) = (\begin{matrix} 1 \\ 0 \\ 0 \end{matrix})$

$u_{2} = b = (\begin{matrix} 0 \\ - 1 \\ 0 \end{matrix})$

この2つの単位ベクトルを用いて、 $c$ を正規直交基底 $v_{3}$ に変換する。

$\begin{aligned} (1) & v_{3} & = (\begin{array}{c} 2 \\ 2 \\ 2 \end{array}) - ((\begin{array}{c} 1 \\ 0 \\ 0 \end{array}) \cdot (\begin{array}{c} 2 \\ 2 \\ 2 \end{array})) \cdot (\begin{array}{c} 1 \\ 0 \\ 0 \end{array}) - ((\begin{array}{c} 0 \\ - 1 \\ 0 \end{array}) \cdot (\begin{array}{c} 2 \\ 2 \\ 2 \end{array})) \cdot (\begin{array}{c} 0 \\ - 1 \\ 0 \end{array}) \\ (2) & = (\begin{array}{c} 2 \\ 2 \\ 2 \end{array}) - (\begin{array}{c} 1 \\ 0 \\ 0 \end{array}) - (\begin{array}{c} 0 \\ 1 \\ 0 \end{array}) \\ (3) & = (\begin{array}{c} 0 \\ 0 \\ 2 \end{array}) \end{aligned}$

$v_{3}$ を単位ベクトル $u_{3}$ に変換すると、 $u_{3} = (\begin{matrix} 0 \\ 0 \\ 1 \end{matrix})$

よって、求める正規直交基底 $u_{1}, u_{2}, u_{3}$ は、 $u_{1} = (\begin{matrix} 1 \\ 0 \\ 0 \end{matrix}), u_{2} = (\begin{matrix} 0 \\ - 1 \\ 0 \end{matrix}), u_{1} = (\begin{matrix} 0 \\ 0 \\ 1 \end{matrix})$