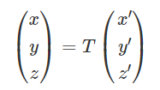【2次形式】標準形の変換問題

例題

対称行列 $A = (\begin{matrix} 3 & 1 & 1 \\ 1 & 3 & 1 \\ 1 & 1 & 3 \end{matrix})$ を用いて、関数 $f (x, y, z) = 3 x^{2} + 3 y^{2} + 3 z^{2} + 2 x y + 2 y z + 2 z x$ を標準形 $f (x^{'}, y^{'}, z^{'}) = A x^{2} + B y^{2} + C z^{2}$ に変換せよ。

2次形式とは
本記事で覚えたいこと
解答例
最後に
追記(発展問題)

2次形式とは

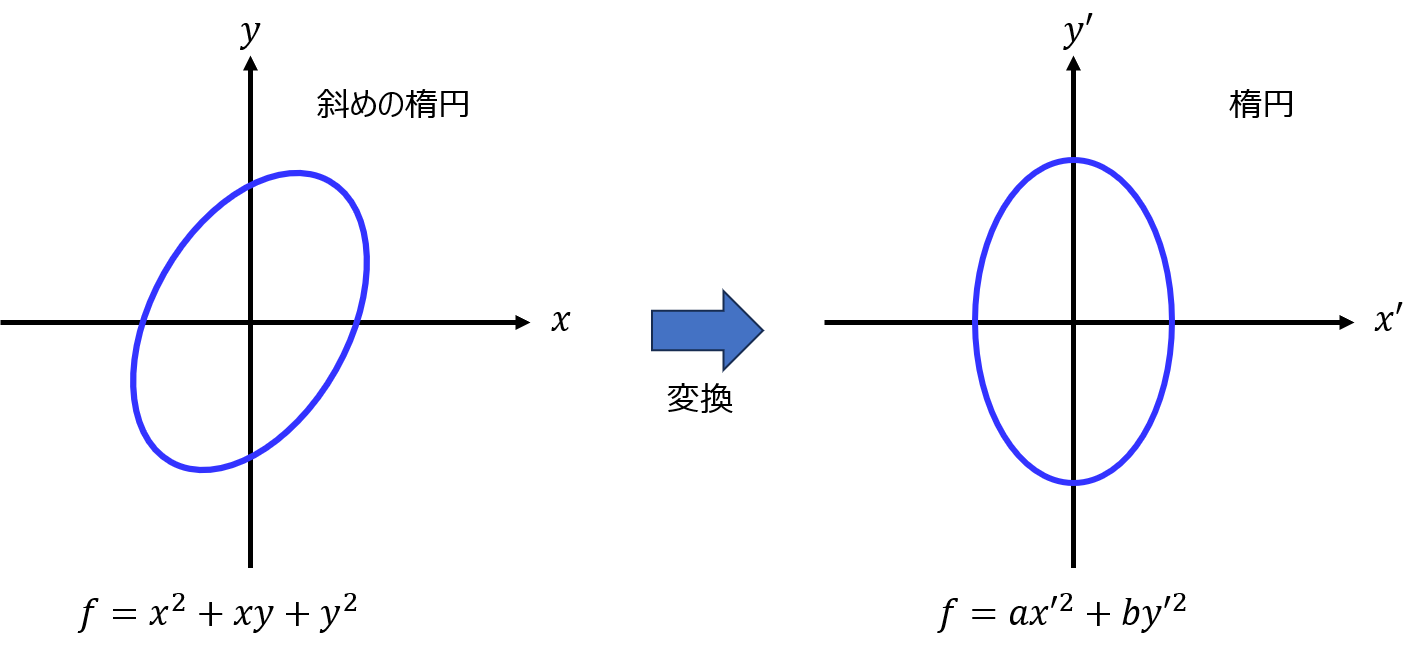
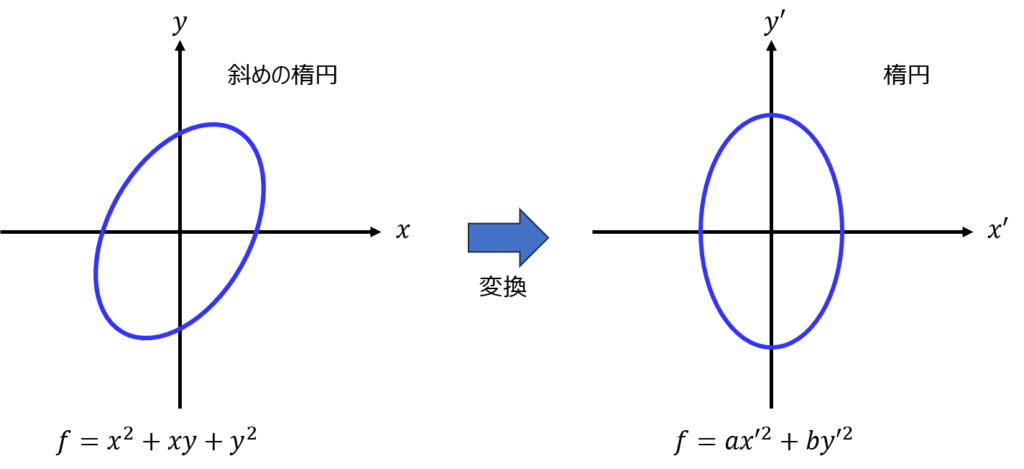
斜めの楕円を楕円形に変換することです。

例題の関数は、xy項が混じっています。この影響でグラフにプロットすると斜めの形になっていますが、座標軸を適切に変換することで、x,y軸に対して対称な楕円形に変換できます。

院試では、標準形に変換した後に、関数の最大最小値、領域の面積を求めることもあります。こちらについては次回以降の記事で紹介します。

本記事で覚えたいこと

$f (x, y, z) = a x^{2} + b y^{2} + c z^{2} + d x y + e y z + f z x$ 型の2次曲線は、 $(\begin{matrix} a & \frac{d}{2} & \frac{f}{2} \\ \frac{d}{2} & h & \frac{e}{2} \\ \frac{f}{2} & \frac{e}{2} & c \end{matrix})$ で表すことができる。
対称行列Aを直交行列Tを用いて、 $T^{t} A T^{t} = D$ と対角化する。(ただし、Tの各列ベクトルは正規直交基底であること)
$D = (\begin{matrix} λ_{1} & 0 & 0 \\ 0 & λ_{2} & 0 \\ 0 & 0 & λ_{3} \end{matrix})$ のとき、 $f (x^{'}, y^{'}, z^{'}) = λ_{1} x^{2} + λ_{2} y^{2} + λ_{3} z^{3}$ と標準形変換できる。

どれも重要ですが、1番目の事項(行列の形)については是非とも押さえておきたいです。与えられた2次曲線を、 $x^{t} A x$ で表そうとすると導出できます。

他、3番目の事項については、以下の関係式から標準形変換できます。

$f (x, y, z) = x^{t} A x = (T x^{'})^{t} A (T x) = x^{' t} T^{t} A T x^{'} = x^{' t} D x^{'} = λ_{1} x^{2} + λ_{2} y^{2} + λ_{3} z^{3}$

特に、 $x = T x^{'}$ で座標変換することがミソです。2式目→3式目と変更する部分に使用しています。

このように変換することで、対角行列与えられた2次形式を対角行列 $D$ を用いたシンプルなものに置き換えることができます。

解答例

与えられた対称行列 $A = (\begin{matrix} 3 & 1 & 1 \\ 1 & 3 & 1 \\ 1 & 1 & 3 \end{matrix})$ は、関数 $f (x, y, z)$ の2次形式である。

よって、 $A$ を対角化し、対角行列 $D$ を求める。固有値を $λ$ とすると、行列式は

$\begin{aligned} (1) & | \begin{array}{c} 3 - λ & 1 & 1 \\ 1 & 3 - λ & 1 \\ 1 & 1 & 3 - λ \end{array} | \\ (2) & = - λ^{3} + 9 λ^{2} - 24 λ + 20 \\ (3) & = - (λ - 2) (λ^{2} - 7 λ + 10) \\ (4) & = - (λ - 2)^{2} (λ - 5) \end{aligned}$

以上より、固有値は $λ = 2$ (重解)、 $5$

(i) $λ = 2$ のとき、固有ベクトルは、 $x + y + z = 0$ より、 $p_{1} = (\begin{matrix} - 1 \\ 0 \\ 1 \end{matrix}), p_{2} = (\begin{matrix} - 1 \\ 1 \\ 0 \end{matrix})$

$p_{1} ･ p_{2} \neq 0$ より、正規直交基底にすることを考える。

まず、 $p_{1}$ を単位ベクトル $v_{1}$ に変換すると、 $v_{1} = (\begin{matrix} \frac{- 1}{\sqrt 2} \\ 0 \\ \frac{1}{\sqrt 2} \end{matrix})$

次に、 $v_{1}$ の直交行列 $u_{2}$ を考える。グラムシュミットの直交化法より

$\begin{aligned} (5) & u_{2} & = p_{2} - (p_{2} ･ v_{1}) v_{1} \\ (6) & = (\begin{array}{c} - 1 \\ 1 \\ 0 \end{array}) \cdot ((\begin{array}{c} - 1 \\ 1 \\ 0 \end{array}) \cdot \frac{1}{\sqrt 2} (\begin{array}{c} - 1 \\ 0 \\ 1 \end{array})) \cdot \frac{1}{\sqrt 2} (\begin{array}{c} - 1 \\ 0 \\ 1 \end{array}) \\ (7) & = (\begin{array}{c} - 1 \\ 1 \\ 0 \end{array}) - \frac{1}{2} (\begin{array}{c} - 1 \\ 0 \\ 1 \end{array}) \\ (8) & = (\begin{array}{c} \frac{- 1}{2} \\ 1 \\ \frac{1}{2} \end{array}) \end{aligned}$

これを単位ベクトルにすると、 $v_{2} = \frac{1}{\sqrt 6} (\begin{matrix} - 1 \\ 2 \\ - 1 \end{matrix})$

(ii) $λ = 5$ のとき、固有ベクトルは、 $(\begin{matrix} 1 \\ 1 \\ 1 \end{matrix})$ で、単位ベクトル $v_{3} = (\begin{matrix} \frac{1}{\sqrt 3} \\ \frac{1}{\sqrt 3} \\ \frac{1}{\sqrt 3} \end{matrix})$ になる。

$v_{1} ･ v_{2} = v_{2} ･ v_{3} = v_{3} ･ v_{1} = 0$ より、それぞれの列ベクトルは正規直交基底である。

よって、 $T = (\begin{matrix} \frac{- 1}{\sqrt 2} & \frac{- 1}{\sqrt 6} & \frac{1}{\sqrt 3} \\ 0 & \frac{2}{\sqrt 6} & \frac{1}{\sqrt 3} \\ \frac{1}{\sqrt 2} & \frac{- 1}{\sqrt 6} & \frac{1}{\sqrt 3} \end{matrix})$ とすると

$(\begin{matrix} x \\ y \\ z \end{matrix}) = T (\begin{matrix} x^{'} \\ y^{'} \\ z^{'} \end{matrix}) = (\begin{matrix} \frac{- 1}{\sqrt 2} & \frac{- 1}{\sqrt 6} & \frac{1}{\sqrt 3} \\ 0 & \frac{2}{\sqrt 6} & \frac{1}{\sqrt 3} \\ \frac{1}{\sqrt 2} & \frac{- 1}{\sqrt 6} & \frac{1}{\sqrt 3} \end{matrix}) (\begin{matrix} x^{'} \\ y^{'} \\ z^{'} \end{matrix})$ に変換できる。