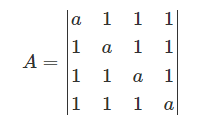対角成分のみ異なる行列の行列式の演算

下記の行列1,2の固有値を求めよ。
<行列1>
$$\begin{array}{}\text{(1)}& A=\left|\begin{array}{cccc}a& 1& 1& 1\\ 1& a& 1& 1\\ 1& 1& a& 1\\ 1& 1& 1& a\end{array}\right|\end{array}$$
<行列2>
$$\begin{array}{}\text{(2)}& {\displaystyle \frac{1}{2}}\left|\begin{array}{ccc}a+b+c& -c& -b\\ -c& a+b+c& -a\\ -b& -a& a+b+c\end{array}\right|\end{array}$$

はじめに

こちらの問題、まじめに計算すると途方もない時間がかかります。1行目をサラスの式で3*3行列に展開し、演算を続ける。。。限りある試験時間で行うものではありません。

にもかかわらず、大学によっては意外と上記の形式の行列は出てきます。こういったときに効率よく計算する方法を本記事では紹介します。

本問で覚えたいこと

下記のように、工夫して行列式を求めます。

特に重要な項目は一番目(列基本変形)です。固有ベクトルを求める問題ばかり行っているといつの間にか抜けている方もいらっしゃるかもしれません。

確かに、固有ベクトルの計算(連立方程式を解く)に対しては使えないのですが、行列式の演算では列基本変形を行っても問題ないことは教科書で説明されています。詳しい説明は、他の文献にお任せするとし、本記事では標記の問題を実際に解いてみます。

解答例 <行列1>

固有値を$\lambda$とし、$|A-\lambda E|$を考える。

$$\begin{array}{}\text{(3)}& & \left|\begin{array}{cccc}a-\lambda & 1& 1& 1\\ 1& a-\lambda & 1& 1\\ 1& 1& a-\lambda & 1\\ 1& 1& 1& a-\lambda \end{array}\right|& \text{(4)}& & =\left|\begin{array}{cccc}a-\lambda +3& 1& 1& 1\\ a-\lambda +3& a-\lambda & 1& 1\\ a-\lambda +3& 1& a-\lambda & 1\\ a-\lambda +3& 1& 1& a-\lambda & \end{array}\right|\text{(5)}& & =\left|\begin{array}{cccc}a-\lambda +3& 1& 1& 1\\ 0& a-\lambda -1& 0& 0\\ 0& 0& a-\lambda -1& 0\\ 0& 0& 0& a-\lambda -1\end{array}\right|\end{array}$$

(4)式まで変形した結果、１列目が１行目以外全て0になりました。これならば、簡単に固有値を求められそうです。

補足として、１式目→２式目で列基本変形。２式目→３式目で行基本変形しています。

続きに行きます。

(4)式をサラスの公式を用いて変形すると

$$\begin{array}{}\text{(6)}& & (a-\lambda +3)\left|\begin{array}{ccc}a-\lambda -1& 0& 0\\ 0& a-\lambda -1& 0\\ 0& 0& a-\lambda -1\end{array}\right|& \text{(7)}& & =(a-\lambda +3)(a-\lambda -1{)}^3& \text{(8)}& & =0& \end{array}$$

よって、求める固有値は、$\lambda =a+3,a-1$(重解)

解答例 <行列2>

列基本変形と行基本変形を駆使します。行列1のように、１列目に全ての要素を足し合わせると解決するわけではありません。下記の手順で行います。

複数箇所を列基本変形し、最後に行基本変形することがポイントです。対称式のため、上手い具合に余分な項が打ち消しあい、因数を作れる形になります。

まず、手順1に基づいて列基本変形する。

$$\begin{array}{}\text{(9)}& & {\displaystyle \frac{1}{2}}\left|\begin{array}{ccc}a+b+c& -c& -b\\ -c& a+b+c& -a\\ -b& -a& a+b+c\end{array}\right|\text{(10)}& & ={\displaystyle \frac{1}{2}}\left|\begin{array}{ccc}a+b& -(b+c)& -b\\ a+b& b+c& -a\\ -(a+b)& b+c& a+b+c\end{array}\right|\text{(11)}& & ={\displaystyle \frac{1}{2}}(a+b)(b+c)\left|\begin{array}{ccc}1& -1& -b\\ 1& 1& -a\\ -1& 1& a+b+c\end{array}\right|\end{array}$$

手順2により、3行目を1行目に足し、展開すると

$$\begin{array}{}\text{(12)}& & {\displaystyle \frac{1}{2}}(a+b)(b+c)\left|\begin{array}{ccc}0& 0& a+c\\ 1& 1& -a\\ -1& 1& a+b+c\end{array}\right|\text{(13)}& & ={\displaystyle \frac{1}{2}}(a+b)(b+c)(a+c)\left|\begin{array}{cc}1& 1\\ -1& 1\end{array}\right|\text{(14)}& & =(a+b)(b+c)(a+c)\end{array}$$

を得られた。

最後に

標記の問題で紹介した行列は、n*n行列の場合、n-1個の重解を持つことが多いです。問題によっては、ここから固有ベクトルを求め、ジョルダン標準形なども使用して対角化することも求められたりします。このようなケースは後の記事でご紹介できればと思います。

参考文献

入門線形代数：三宅 敏恒(著) 第3章 P60