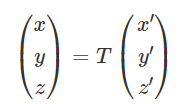【2次形式】標準形の変換問題(領域の面積算出)

問題

対称行列 $A = (\begin{matrix} 3 & 1 & 1 \\ 1 & 3 & 1 \\ 1 & 1 & 3 \end{matrix})$ を用いて、関数 $f (x, y, z)$ を以下のように変換した。 $\begin{array}{r} (1) & f (x, y, z) = 3 x^{2} + 3 y^{2} + 3 z^{2} + 2 x y + 2 y z + 2 z x \end{array}$ $\begin{array}{r} (2) & f (x^{'}, y^{'}, z^{'}) = 2 x^{2} + 2 y^{2} + 5 z^{2} \end{array}$

(1) $x, y, z$ の取りうる値の関係が $x^{2} + y^{2} + z^{2} = 1$ であるとき、元の関数 $f (x, y, z)$ の取りうる値の最大値、最小値を求めよ。
(2) $x, y, z$ の取りうる領域Dが、 $D = {(x, y, z) | x^{2} + y^{2} + z^{2} ≦ 1}$ であるとき、元の関数 $f (x, y, z)$ が取りうる体積を求めよ。

ただし、変換行列を、 $T = (\begin{matrix} \frac{- 1}{\sqrt 2} & \frac{- 1}{\sqrt 6} & \frac{1}{\sqrt 3} \\ 0 & \frac{2}{\sqrt 6} & \frac{1}{\sqrt 3} \\ \frac{1}{\sqrt 2} & \frac{- 1}{\sqrt 6} & \frac{1}{\sqrt 3} \end{matrix})$ とする。

はじめに
本記事で覚えたいこと
解答例
最後に

はじめに

行列の2次形式に関する問題の続きです。前回は、与えられた2次形式の関数を楕円形に変換しました。

本記事では、 $x^{2} + y^{2} + z^{2} = 1$ の条件の下、関数f(x,y,z)が取りうる最大、最大値について考察します。最後に、楕円形が囲む領域を関数に代入した時の面積を求めます。

本記事で覚えたいこと

座標系 $(x, y, z) \to (x^{'}, y^{'}, z^{'})$ の変換行列

$\begin{array}{r} (3) & (\begin{array}{c} x \\ y \\ z \end{array}) = T (\begin{array}{c} x^{'} \\ y^{'} \\ z^{'} \end{array}) \end{array}$ を用いることがキーポイントになります。

最大、最小問題

標準形に変換後の関数 $f (x^{'}, y^{'}, z^{'})$ で最大、最小を与える $(x^{'}, y^{'}, z^{'})$ を求める。
(3)式に求めた $(x^{'}, y^{'}, z^{'})$ を代入。これを解くことで、 $(x, y, z)$ 領域に逆変換する。

最大、最小値を求めやすい座標系 $(x^{'}, y^{'}, z^{'})$ で値を求め、それを変換行列を用いて元の座標系に戻す方針で答えを求めます。

領域の面積(体積)を求める問題

楕円体の体積の公式( $V = \frac{4}{3} π a b c)$ を用いて、座標変換後の関数 $f (x^{'}, y^{'}, z^{'})$ の体積を求める
座標変換前後の基本ベクトル(x,x’,y,y’,z,z’)で、長さが変わっているものがあるかチェック。
正規直交基底の場合は基本ベクトルの長さが変わらないので、１．の算出結果が座標変換前の関数に対しても使える。

１．の公式を知っているかが、この問題を解く可能性を左右します。

媒介変数表示などを使えば知っていなくても解けるはずですが、当然計算量が多くなります。

そこで、変換行列を使用すると楕円になることが予想できます。これを利用することで、楽に計算することができます。

解答例

(1)最大、最小値問題

$x^{2} + y^{2} + z^{2} = 1$ が、座標変換後の $(x^{'}, y^{'}, z^{'})$ で取りうる値の関係式を考える。

問題で与えられた変換行列 $T$ より、以下の関係式を導ける。

$\begin{matrix} (4) & {\begin{cases} x = - \frac{x^{'}}{\sqrt{2}} - \frac{y^{'}}{\sqrt{6}} + \frac{z^{'}}{\sqrt{3}} \\ y = 0 + \frac{2}{\sqrt{6}} y^{'} + \frac{z^{'}}{\sqrt{3}} \\ z = \frac{x^{'}}{\sqrt{2}} - \frac{y^{'}}{\sqrt{6}} + \frac{z^{'}}{\sqrt{3}} \end{cases} \end{matrix}$

これを $x^{2} + y^{2} + z^{2} = 1$ に代入すると、 $x^{' 2} + y^{2} + z^{' 2} = 1$ となり、元の関係式と同じになる。

※正規直交基底なので、変換後も同じ関係式になります。不安ならば、検算してみると良いかもしれません。

$x^{' 2} + y^{' 2} = 1 - z^{' 2} を$ (2)式に代入すると、以下のようになる。

$\begin{aligned} (5) & (2) & = 2 (1 - z^{' 2}) + 5 z^{' 2} \\ (6) & = 2 + 3 z^{' 2} \end{aligned}$

最大、最小を求めるには、 $z^{'}$ の取りうる値に注意すれば良く

$(x^{'}, y^{'}, z^{'}) = (0, 0, \pm 1) \Leftrightarrow (x, y, z) = (\pm \frac{1}{\sqrt 3}, \pm \frac{1}{\sqrt 3}, \pm \frac{1}{\sqrt 3})$ のとき、最大値5

$(x^{'}, y^{'}, z^{'}) = (\cos θ, \sin θ, 0) \Leftrightarrow x + y + z = 0)$ のとき、最小値2

※x+y+z=0の関係を導くには、(x’,y’,z’)それぞれの値を(4)式に代入すればよいです。

(2)面積(体積の計算問題)

前節により、 $x^{2} + y^{2} + z^{2} ≦ 1$ を座標変換すると、同じく $x^{' 2} + y^{' 2} + z^{2} ≦ 1$ になることが分かる。よって、座標変換後の変数 $x^{'}, y^{'}, z^{'}$ の取りうる領域は、変換前と変わらない。

また、変換前後の基本ベクトル(x,x’,y,y’,z,z’)は両方正規直交基底であるため、変換後の関数で求めた体積は、変換前の関数の体積と一致する。

変換後の関数は $f (x^{'}, y^{'}, z^{'}) = 2 x^{2} + 2 y^{2} + 5 z^{2}$ であるため、これを楕円体の公式に適用できる形に変形する。

$\frac{x^{2}}{{(\frac{1}{\sqrt{2}})}^{2}} + \frac{y^{2}}{{(\frac{1}{\sqrt{2}})}^{2}} + \frac{z^{2}}{{(\frac{1}{\sqrt{5}})}^{2}} ≦ 1$ で表せるため、求める体積 $V$ は

$\begin{array}{r} (7) & V = \frac{4}{3} π \frac{1}{\sqrt{2}} \frac{1}{\sqrt{2}} \frac{1}{\sqrt{5}} = \frac{2 π}{3 \sqrt 5} \end{array}$

ただし、楕円体の取る範囲は、 $(\frac{- 1}{\sqrt 2} ≦ x^{'} ≦ \frac{- 1}{\sqrt 2}), (\frac{- 1}{\sqrt 2} ≦ y^{'} ≦ \frac{- 1}{\sqrt 2}), (\frac{- 1}{\sqrt 5} ≦ z^{'} ≦ \frac{- 1}{\sqrt 5}$ )