試験範囲
専門科目1は、応用数学、半導体デバイス、電磁気学、電気回路、電子回路からなります。
標準的な難易度ではありますが、試験範囲が広いです。このため、対策に時間がかかります。
北大 情報科学研究院 情報エレクトロニクスコース 院試の全体
専門科目Ⅰ、専門科目Ⅱで分かれています。専門科目Ⅰは、本記事で紹介するように学部2年までの内容で解けてしまう問題が多いです。
一方で、専門科目Ⅱは、量子力学などの専門科目を深く問われています。
自分の得意分野にもよりますが、専門科目Ⅰで点数を確保する作戦の方が、基本的に良いでしょう。
- 応用数学
- 線形代数(毎年出題)
- フーリエ級数(年度による)
- ラプラス変換(年度による)
- ベクトル解析(年度による)
- 微分方程式(年度による)
- 半導体デバイス:
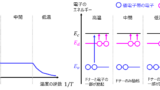
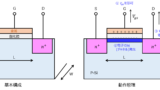
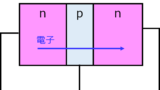
- バンド構造(PN接合、MOSFET)
- ドレイン電流の算出
- 光電流の算出、動作原理
- 電磁気学(次回の記事で説明)
- 電気回路学(同上)
- 電子回路学(同上)
120分で3題選択のため、一題にかけられる時間は40分程度です。
全体的な難易度ですが、応用数学は難しいと思います。(相対的に見て)
冒頭で説明した通り、問題の難易度については大差が無いですが、試験範囲が広いです。5分野出題可能性がありますが、それぞれ一つの講義に相当するため、2*5=10単位分のボリュームに相当します。
一方で、半導体デバイスは2単位が基本で、多くても4単位分の範囲です。試験範囲的にこちらの選択が良いと考えます。
強いて選ぶならば、他の専攻から本コースを受験し、電気系の科目を履修していない場合は使えるかもしれません。また、内部では数学の選択が多い場合は合わせた方が良いかもしれません。(研究室訪問の際に聞いてみましょう)
半導体デバイスは、他大学院でも出題されるような、オーソドックスな出題です。バンド構造が多いので、是非対策しましょう。
本サイトでも、いくつか取り上げています。
光電流だけは、北大特有の出題と言えます。これだけは、参考書を使用するなどし、個別の対策が必要です。
説明問題も毎年1問程度出ます。ただ問題を解くだけでなく、内容を説明できるだけの理解が必要です。
金属-半導体接合はあまり出ないようです。(MOSFETの出題が主)
全体
最近3年分は以下の分野の出題がありました。
- 2023年(応用数学):
- 線形代数:正規直交基底と転置行列、逆行列
- フーリエ級数展開:矩形波の計算
- ラプラス変換:微分方程式の計算
- 2023年(半導体デバイス):
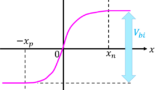
- PN接合のエネルギーバンド図
- MOSFETのドレイン電流値の導出
- 直接遷移型半導体の発行波長。半導体レーザーとLEDの違い。
- 2022年(応用数学):
- 変数変換を利用した微分方程式の一般解
- sin波のフーリエ級数展開
- ベクトル場の線積分
- 2022年(半導体デバイス):
- MOSFETのバンド構造。ビルトインポテンシャルの計算。
- MOSFETのコンダクタンスの計算
- 2021年(応用数学):
- オイラー型微分方程式の一般解
- 三角波と矩形波のフーリエ級数展開
- 直交行列の算出(選択問題)
- ベクトル場の回転、発散の算出(選択問題)
- 2021年(半導体デバイス):
- pn接合半導体のバイアス電圧の変化による振る舞いの説明。光電流の波長。
- MOSFETのエネルギーバンド図の図示。相互コンダクタンスと微細化に対する説明。
応用数学について、微分方程式は変数変換を利用することが多いです。オイラー型微分方程式が特にそうなので、市販の参考書で練習していきましょう。
線形代数、フーリエ級数展開、ベクトル解析、ラプラス変換は、基本的に計算が正確にできれば問題なく得点できると思います。
半導体デバイス:PN接合とMOSFETが頻出になっています。上記で説明した記事を用いて、是非動作原理を理解しておきましょう。
相互コンダクタンスの定義について聞かれることが多いので、これは教科書の内容を暗記しましょう。
教科書(応用数学)
基本的に、市販の演習書を網羅的に練習していくと良いです。院試向けの本など、難しい内容にまで手を出す必要は無いと考えます。
線形代数、ベクトル解析
一般的な大学では、教養科目に属するため、工学部で統一されている教科書は無いです。しかし、北大では応用数学Ⅰ(線形代数とベクトル解析)として、専門科目としてシラバスがありました。
ですので、そこで紹介されている教科書を上げます。
技術者のための高等数学 (2) 線形代数、ベクトル解析 E. クライツィグ (著), Erwin Kreyszig (原名), 堀 素夫 (翻訳) (シラバス対象本)
元は洋書のため、基本的な事項を細かく説明しています。和書だと数行で終わってしまう内容が、1,2ページはザラです。基本的な問題の理解を重視する北大院試に沿った内容と思います。
懸念点は、演習問題に対する解答があまり無いことです。洋書あるあるですが、下記の本などを使用し、補強した方が良いかもしれません。
演習 線形代数 寺田 文行 (著)
成分計算、転置行列、逆行列の計算など、基本的な事項が問われることが多いです。前半の章を中心に勉強し、表現行列、2次形式など難しい分野が並ぶ後半は、最低限で良いでしょう。
演習 ベクトル解析キャンパス・ゼミ 馬場 敬之 (著)
他大学でよく問われる複雑な系での面積分の出題が少ないです。基本的な計算ができれば得点は難しくないと考えますので、もれなく演習できるマセマをオススメします。
微分方程式、フーリエ級数、ラプラス変換
シラバスを確認すると、「応用数学Ⅱ」という科目にて取り上げられているようです。
図解による微分方程式 / 阿部寛治 著 (シラバス対象本)
「微分方程式を解くこと」を題材としていますが、その解き方の一つとしてフーリエ級数、ラプラス変換を説明しています。今の本には無い面白い章立てです。
実際、フーリエ級数、ラプラス変換で本格的な問題が出題されることは近年無いです。よって、本教科書を勉強することが北大対策にとって正しいのかもしれません。
他大学を受ける際は、フーリエ級数とラプラス変換の分野は力不足です。他教科書でのさらなる対策をオススメします。
他、演習書は下記を取り下げます。
演習 微分方程式 寺田 文行 (著), 坂田 ひろし (著)
線形代数と同じ作者の方ですが、それでもお勧めしたい本です。微分方程式の型を網羅的に取り上げられており、適切な分量で演習できます。
前半の章に基本的な型が集中していますので、その部分の演習で良いと考えます。
ラプラス変換、フーリエ級数は計算問題中心です。よって、読者自身のお持ちの教科書で練習することをオススメします。
教科書(半導体デバイス)
「電子デバイス工学」という講義が院試対象科目に当たるようです。そこで紹介されているシラバス教科書を挙げます。
※半導体デバイスも、科目としては存在していましたが、電子デバイス工学の続論のようです。やや発展的な科目のようなので、電子デバイス工学を中心として説明していきます。
電子デバイス工学(第2版・新装版) 古川 静二郎 (著), 荻田 陽一郎 (著), 浅野 種正 (著) (シラバス対象本)
最近出版された本のため、見やすいレイアウトになっています。内容としては、特筆すべき内容はありません。自身で既に教科書をお持ちであれば、そちらを使用しても良いと思います。
他、筆者は下記の本をオススメします。
絵から学ぶ半導体デバイス工学 谷口 研二 (著), 宇野 重康 (著) (シラバス対象本)
バンド構造の図示を勉強していく上で、本書が一番分かりやすいです。「絵から学ぶ」表題通りになっています。最後の章では、北大頻出分野の光電流に関する説明もあるところがさらに良いです。(他の教科書では説明が無いこともあるため。)
電子デバイス工学の続論「半導体デバイス」でも紹介されており、シラバス対象本になっています。少し値段が張りますが、半導体に関する研究を志している方は購入をオススメします。
対策に使える他大学の問題
基本的な問題が多いため、教科書の内容を大切にしたいところです。あえて紹介するとしたら、下記です。
- 応用数学
- 線形代数:京大、東工大、阪大、名大、東北大、電通大など
- ベクトル解析:京大(先端数理 専門3)、九大
- 微分方程式:阪大、名大、九大、農工大
- フーリエ級数:阪大
- ラプラス変換:阪大、東北大
- 半導体デバイス
- 東大、阪大、九大、農工大
東北大は、入試時間短縮の影響から、近年院試問題が簡単になっています。腕試しに丁度良いです。
他、農工大も、出題範囲、内容が似通っているため、一見の価値ありです。
他の大学は、そもそも問題が難しかったり、北大の傾向とは異なっています。あまり確認しなくて良いと考えます。
最後に
次の記事で説明する電磁気学、電気回路、電子回路と比較すると、応用数学と半導体デバイスは選択しにくい科目かもしれません。
どちらか1つ、保険として持っておくくらいで良いでしょう。