入力系列1001を検出し、1を出力する順序回路を2つのJKフリップフロップを用いて実現する。状態遷移図、状態遷移表を記載し、それぞれのフリップフロップ\(J_{1},K_{1}\) , \(J_{2},K_{2}\)に対する入力の論理式、出力zの論理式を求めよ。なお、入力信号はxとする。
はじめに
JKフリップフロップは、少なくとも管理人が従事する会社内ではあまり使用されない論理回路です。(他の業界だと全然使われている場合は、大変申し訳ございません。)
入力の保持は、直感的に分かりやすいDフリップフロップを用いることが多いため、資格試験などでJKフリップフロップの問題を久しぶり見たとき、面食らうことがあります。
ネットで調べると、懇切丁寧に説明されているサイトが多数あり、大変感謝しています。
しかし、問題を解くことだけを目的とするならば、もう少しそれに特化した説明ができるのではないかと考えました。
本記事では、一度は学習済みの方がすぐに解きなおせるように、要点をまとめました。
この記事で覚えたいこと
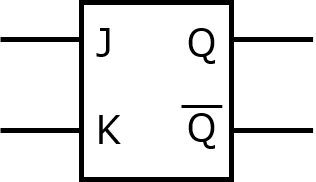
JKフリップフロップの振る舞い
- JKフリップフロップ一つにつき、状態遷移時、1bit分の変化を表現できる。
- 前回値0のときは、J=1で今回値1に遷移する。
- 前回値1のときは、K=1で今回値0に遷移する。
結局、JKフリップフロップの決まり事として、上記さえ覚えていれば何とかなるように思います。
教科書を見ていると、JKフリップフロップの真理値表(特性方程式)として、以下の表1をよく目にします。
定義を重用すると、上記になることは承知しています。
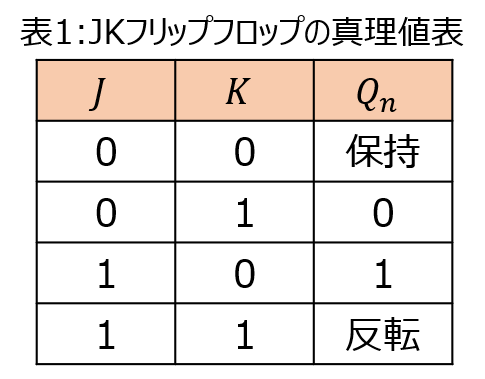
しかし、実用上、\(Q_{n+1}\)はどうなるのか。0,1を入力したとき、結局どのような出力を取るのかと思い出すのに毎回時間がかかってしまいます。
上記の真理値表を書き直すと、下記の表2と等価になります。
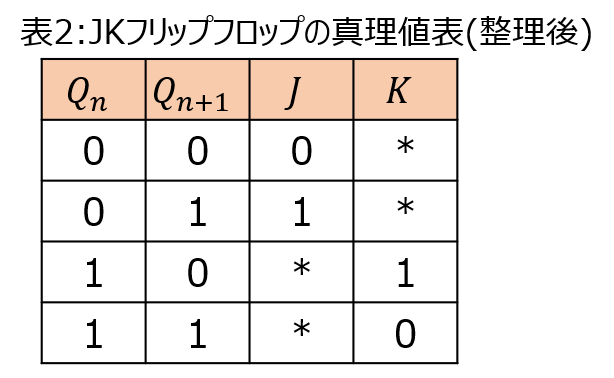
問題を解くうえでは、こちらの方が重要だと考えています。
状態遷移表を作成する際、J、Kに入る値は、 0,1,* のいずれかで記載する必要があり、直接的な表現になっている表2を参照する方が分かりやすいからです。
解法の手順
- 問題で与えられた入力系列を満たす状態遷移図を作成する。
- 状態遷移図を元に状態遷移表を作成。個々の状態を全て表現できるようbit毎に割付する。
- 各bitの0,1の切り替わりをみながら、真理値表2に該当するJ,Kの入力値を決定する。
- カルノー図を使用し、J,Kの入力、出力yの積和最簡形を求める。
手順としては、比較的オーソドックスだと思います。
3番目の手順がJKフリップフロップを用いるがあまり、結局どの値を入力すれば良いのか戸惑いますが、上記の真理値表2が書ければ後は通常の論理回路と変わりません。
解答例
<手順1> 問題で与えられた入力系列1001を満たす状態遷移図を作成する。
今回入力値+過去3回分の入力値を覚えると正しく出力できるので、状態数4=2bitで表現できます。
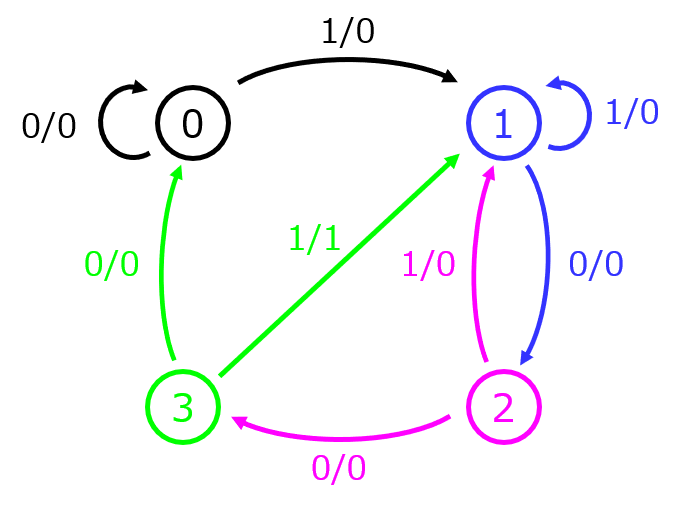
ここで、状態⓪：(0,0) 状態①：(0,1) 状態②：(1,0) 状態③：(1,1)と表します。
<手順2>状態遷移表の作成
手順1で得られた図を素直に表に起こす作業です。
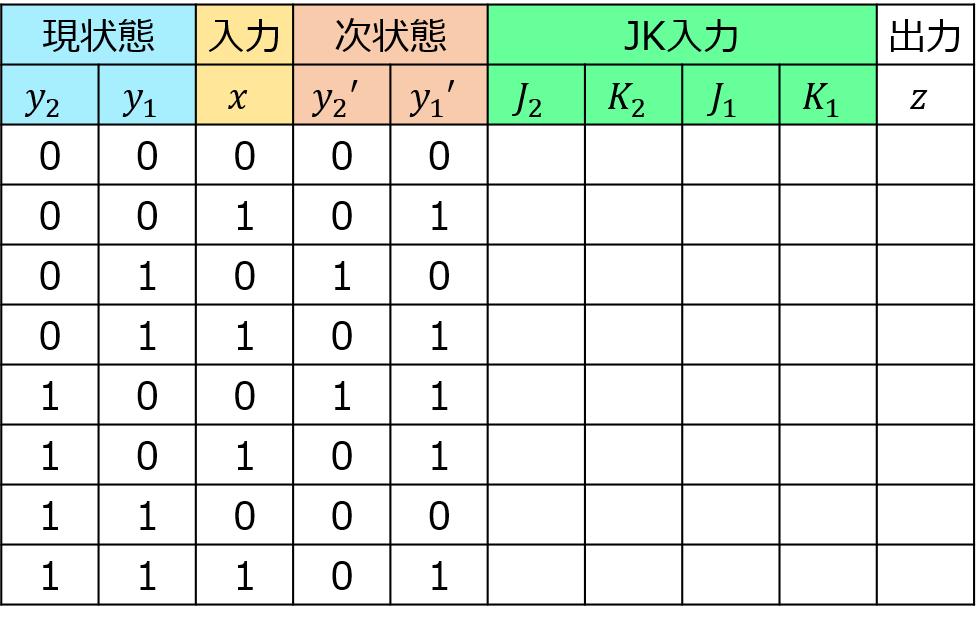
<手順3>JKフリップフロップの入力値の決定
真理値表2に基づいて\(J_{1},K_{1}\) , \(J_{2},K_{2}\)の値を決定します。
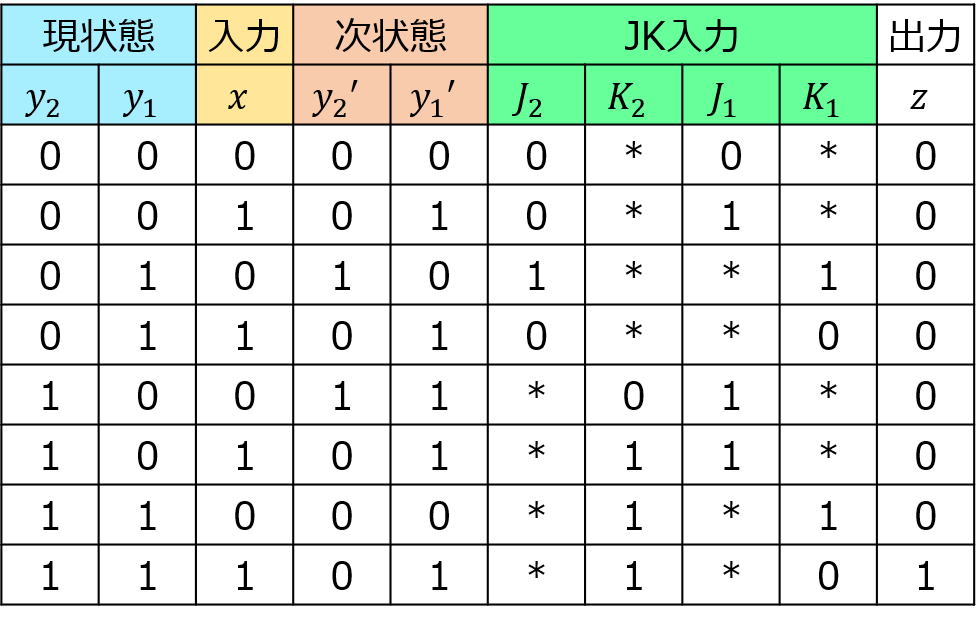
ここまで来れば、答えはすぐです。
<手順4>カルノー図に基づき、論理式を求める。
見間違いによる図作成ミスに注意して
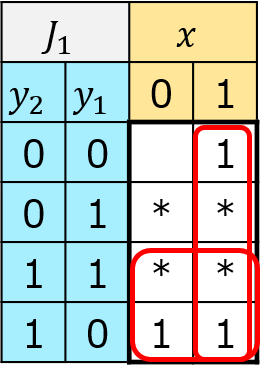
\(J_{1}=x+y_{2}\)
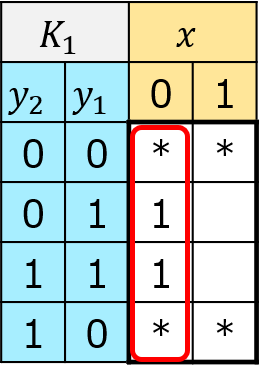
\(K_{1}=\overline{x}\)
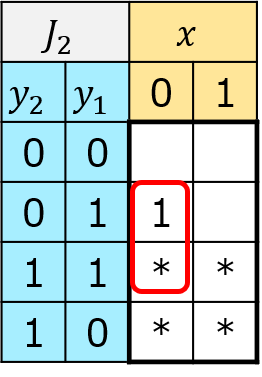
\(J_{2}=\overline{x}y_{1}\)
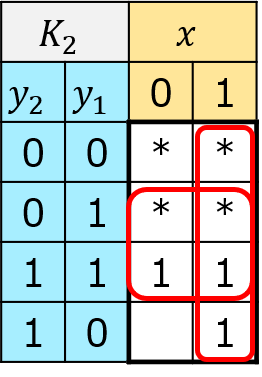
\(K_{2}=x+y_{1}\)
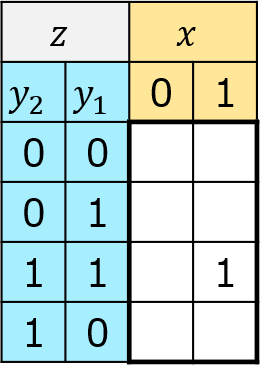
\(z=xy_{1}y_{2}\)
補足：Dフリップフロップを用いたJKフリップフロップの設計
前章のように、J,Kに入る値を正しく判断すると、JKフリップフロップのブロック一つだけで、値の保持及び更新を表現できます。よって、仕様を理解している人が作成すると、シンプルなコードで目的とする演算を実現できます。
しかし、実際の会社では好まれて使っていますでしょうか。管理人の所感ですが、会社によると考えられます。JKFFを知らない方が在籍する会社の場合は、使用することが必ずしも正解とは限りません。
プログラミング経験豊富の社員が多い会社
ベンチャー企業のように、プログラミングが業務を遂行する上でほぼ必須な会社では、JKフリップフロップの動作を理解していることが当たり前かもしれません。
このような現場では、プログラム実装者がJKフリップフロップを使用しても、後で第三者が確認したときに動作を理解できるはずです。よって、使用して問題無いはずです。
プログラミング経験の無い社員も在籍する会社
一方で、大企業のような会社だとどうでしょうか。社員全員がプログラミングを深く理解しているわけではないはずです。管理人の経験では、見慣れない関数を見るだけで、理解を諦める方がいらっしゃいます。
このような方々にも動作を理解いただき、決裁を頂かなければならない場面が多々あります。少しでも理解しやすくするために、私はDフリップフロップを用いて、下記(右図)のような回路を組むことが多いです。
右図の回路の良いところは、更新判断するブロックと、更新する値の算出ブロックが明確に分かれていることです。
左図のJKフリップフロップでは、更新判断と更新する値の判断が同じブロックに混在しており、分かりにくいと感じる人が居ます。ですが、右図の場合だと、二つの判断が別のブロックに分けられており、中央の大ブロックでは、aの条件に応じて出力を変えるだけになります。
これならば、プログラミング経験の無い方に説明するハードルが低くなります。
ソフトウェアエンジニアとしての心構え
院試勉強で、JKフリップフロップの知識が付いたとします。今後のソフト実装で使いたくなるかもしれません。しかし、自分が書いたコードは、他の人が読んでも理解できるものなのか。を是非考えることにしましょう。
不具合の無いコードを出すことと同じレベルで重要です。
最後に
JKフリップフロップに対して否定的な意見が多くなってしまい、大変恐縮です。
管理人の浅学が故、偏った意見になってしまっているのではないかと考えています。
業務上の有益な使い方がある場合は、ご教授下さると大変嬉しく思います。
