下記の真理値表で与えられる論理関数\(f(x_{0},x_{1},x_{2},x_{3})\)を、クワインマクラスキー法(QM法)を用いて簡単化せよ。
真理値表:
| \(x_{0}\) | \(x_{1}\) | \(x_{2}\) | \(x_{3}\) | \(f(x_{0},x_{1},x_{2},x_{3})\) |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
クワインマクラスキー法(QM法)とは
論理関数を簡単化する方法の一つです。
出力1を与える論理変数\(x_{0},x_{1},x_{2},x_{3}\)の組み合わせのうち、一変数だけ数値が異なる組み合わせをマージを繰り返し、簡単化していきます。
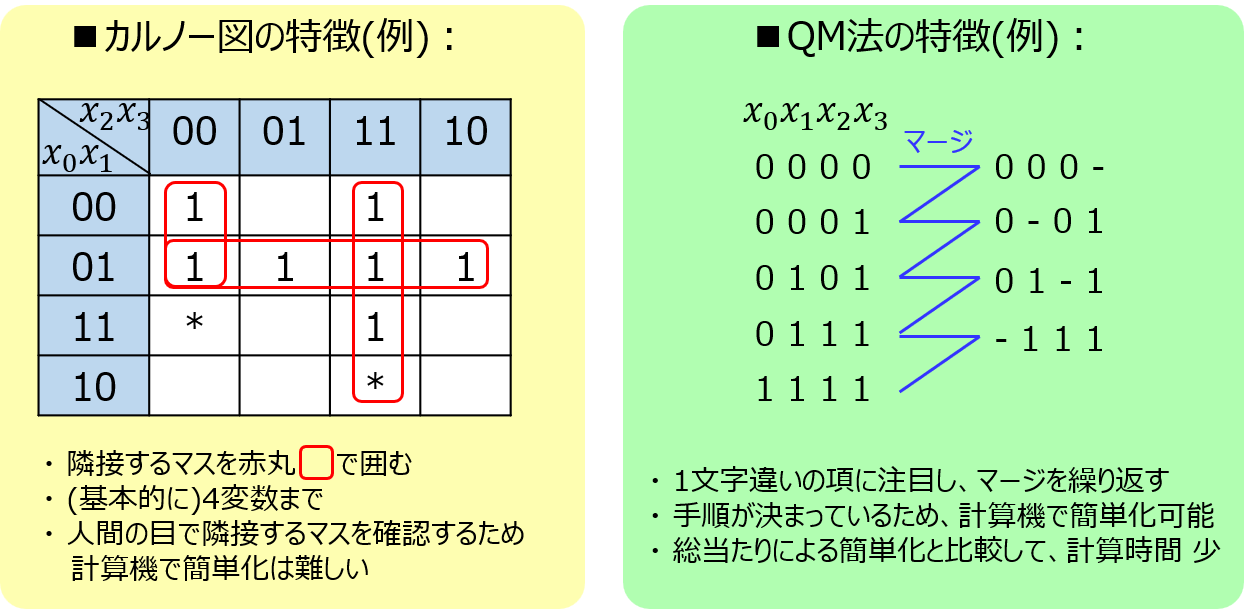
よく、カルノー図を用いた簡単化と比較されることがありますが、下記の利点があります。
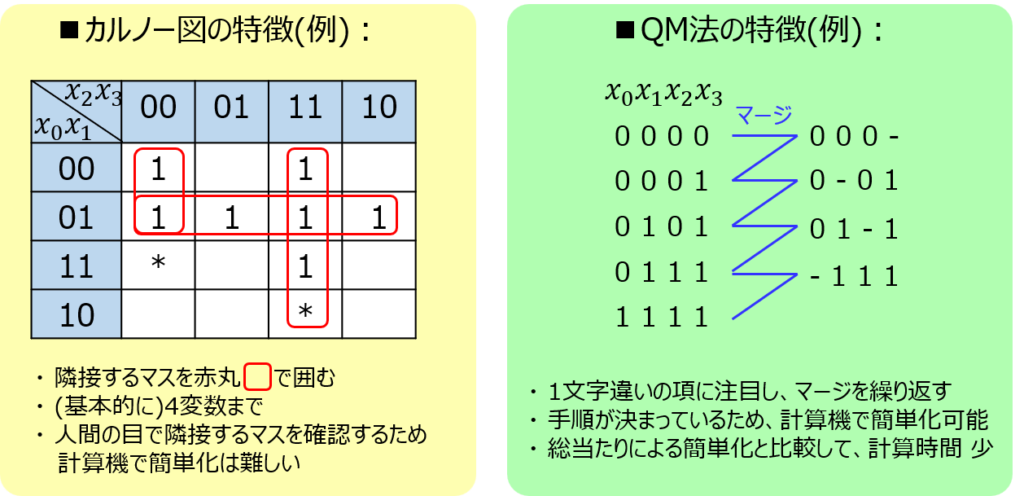
- 任意の入力変数の数の論理変数に対し、簡単化を実施できる
- 簡単化の手順が決まっているため、計算機で機械的に簡単化できる
- 単純な最小項の総当たりに対し、計算時間を低減できる
1.2.はカルノー図に対して優位な項目になります。(利点)
カルノー図は、ハミング距離が1になるマスを作成し、1または※(ドントケア)が隣接しているマスを丸で囲っていく方法になります。
視覚的で、人間の目からすると分かりやすいですが、計算機からするとこの内容を理解することができません。
また、人間の手で行えるのはせいぜい4変数までです。5変数の場合、5変数目の入力0,1ごとにマスを分けて作成すると、何とか対応することもできますが、試験で行うには時間がかかります。
ところが、QM法にはマスの制約が無いため、5変数以上の場合でも問題なく対応できます。
3.について、何も考えずに簡単化しようとすると、\((x_{0},x_{1},x_{2},x_{3})=(0,0,0,0),(1,1,1,1)\)の対応まで確認する必要があります。全ての変数が異なっており、両者を満たす項は明らかに生成できそうにありません。
こういった無駄を、クワインマクラスキー法では初めから省くことができます。
クワインマクラスキー法の手順
- 出力1の論理変数の組み合わせを表にする。
※論理変数に1が含まれる数が少ない順に表にする。 - 入力の組み合わせのうち、互いに1文字違いの項目を探し、ドントケアにマージする。
マージする組み合わせが無くなるまで繰り返す。 - マージ後の主項それぞれに対し、取りうる値を行列表示にする。
- 行列のうち、一つしか1を持たない列に対応する最小項を必須主項にする。
- 必須主項で包含できない出力を持つ最小項を必須項にする。
全ての出力を包含できるようになるまで繰り返す。
実際に、問題を解きながら説明していきます。
解答例
出力1の論理変数の組み合わせを表にする。
問題文で与えられた真理値表のうち、出力1を取る組み合わせだけピックアップすれば良いです。
| 1を取る変数の数 | \(x_{0}\) | \(x_{1}\) | \(x_{2}\) | \(x_{3}\) |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 1 |
| 2 | 1 | 0 | 1 | 0 |
| 3 | 1 | 1 | 0 | 1 |
| 4 | 1 | 1 | 1 | 1 |
入力の組み合わせのうち、互いに1文字違いの項目を探し、ドントケアにマージする。
先ほど作成した表のうち、1を取る変数の個数が1つ違いの行同士を比較します。
その結果、変数の取る値が1文字違いの組み合わせをマージしていきます。
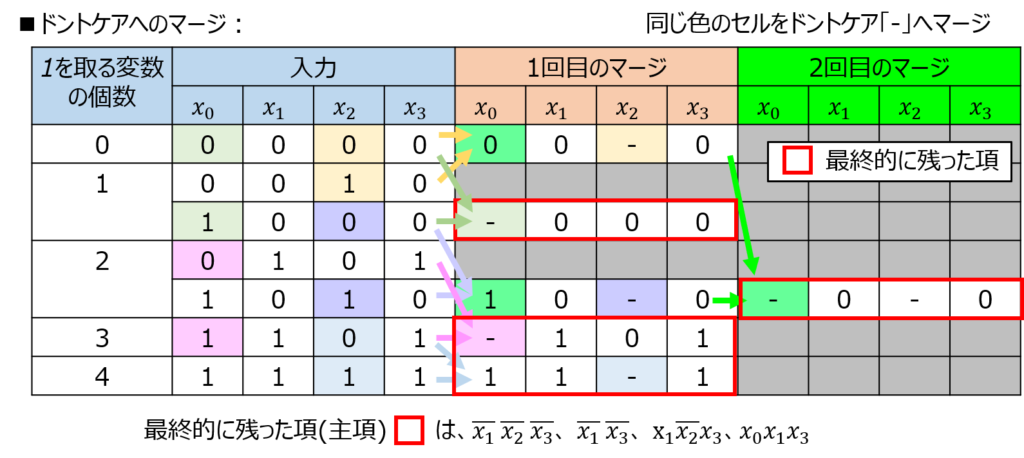
これを繰り返すことで、主項は下記になる。\begin{aligned}\overline{x}_{1}\overline{x}_{2}\overline{x_{3}},\overline{x}_{1}\overline{x_{3}},x_{1}\overline{x}_{2}x_{3},x_{0}x_{1}x_{3}\end{aligned}
マージ後の主項それぞれに対し、取りうる値を行列表示にする。
- \(x_{0}\)は\(2^{0}x_{0}\)で表されるため、入力0,1に対し、出力0,1の2通り
- \(x_{1}\)は\(2^{1}x_{0}\)で表されるため、入力0,1に対し、出力0,2の2通り
- \(x_{2}\)は\(2^{2}x_{0}\)で表されるため、入力0,1に対し、出力0,4の2通り
- \(x_{3}\)は\(2^{3}x_{0}\)で表されるため、入力0,1に対し、出力0,8の2通り
これらを出力として足し合わせると、下記の表が生成される。
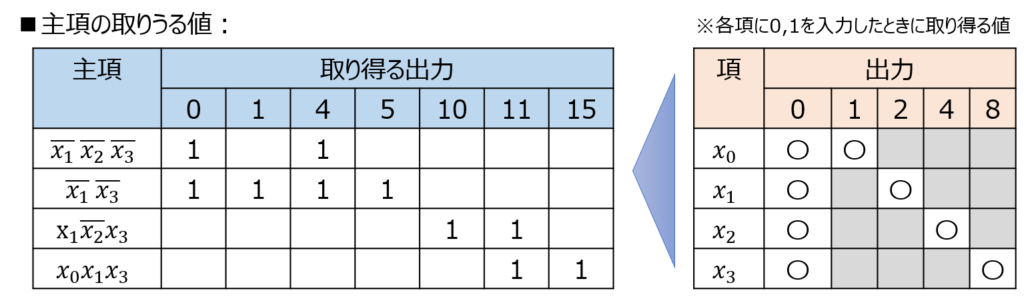
行列のうち、一つしか1を持たない列に対応する最小項を必須主項にする。
前節で得られた表に対し、必須主項を橙色のセルで塗りつぶす。
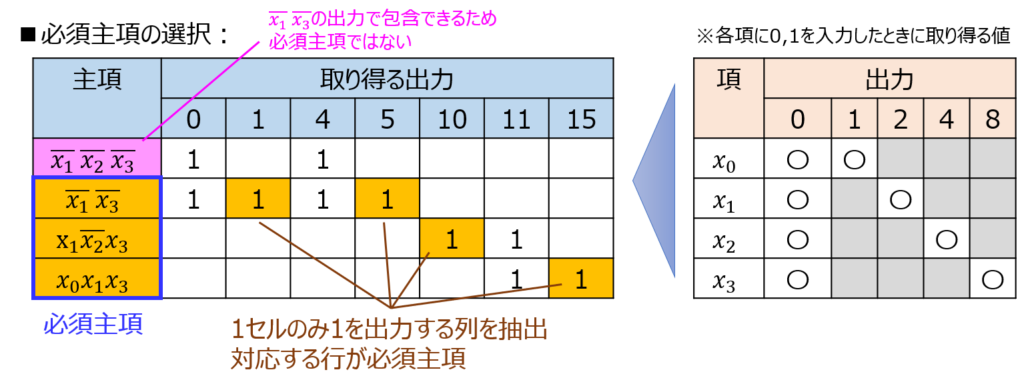
対応する必須主項は、\begin{aligned}\overline{x}_{1}\overline{x_{3}},x_{1}\overline{x}_{2}x_{3},x_{0}x_{1}x_{3}\end{aligned}
ピンク色で塗った\(\overline{x}_{1}\overline{x}_{2}\overline{x_{3}}\)については、\(\overline{x}_{1}\overline{x_{3}}\)で包含できるため、これで全ての出力を包含できた。
結果
前節で得られた必須主項を足し合わせ、求める論理関数は
\begin{aligned}f(x_{0},x_{1},x_{2},x_{3})=\overline{x}_{1}\overline{x_{3}}+x_{1}\overline{x}_{2}x_{3}+x_{0}x_{1}x_{3}\end{aligned}
まとめ
大学によっては、カルノー図ではなく、クワインマクラスキー法を用いての簡単化をわざわざ問うてくることがあります。
カルノー図で簡単化できるから問題ない!と慢心することなく、QM法でもできるようになることをオススメします。