【オイラー法】非線形素子を含んだLR直列回路の過渡解析、連成解析

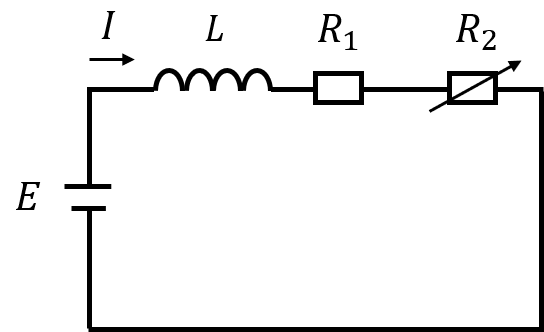
はじめに

電気回路の過渡解析を、オイラー法を用いて行います。

非線形素子$R_2$の無い、一般的なLR直列回路は

回路方程式

$$\begin{array}{}\text{(1)}& E=L{\displaystyle \frac{dI}{dt}}+R_{1}I\end{array}$$が成立し、ラプラス変換を使用すると

$$\begin{array}{}\text{(2)}& I\left(t\right)={\displaystyle \frac{E}{R_1}}(1-e^{-\frac{R_1}{L}t})\end{array}$$

を手計算で難なく導けると思います。

しかし、今回のような、非線形素子$R_2=(\frac{I}{5}{)}^{10}$が入った場合はどうなるのでしょうか。

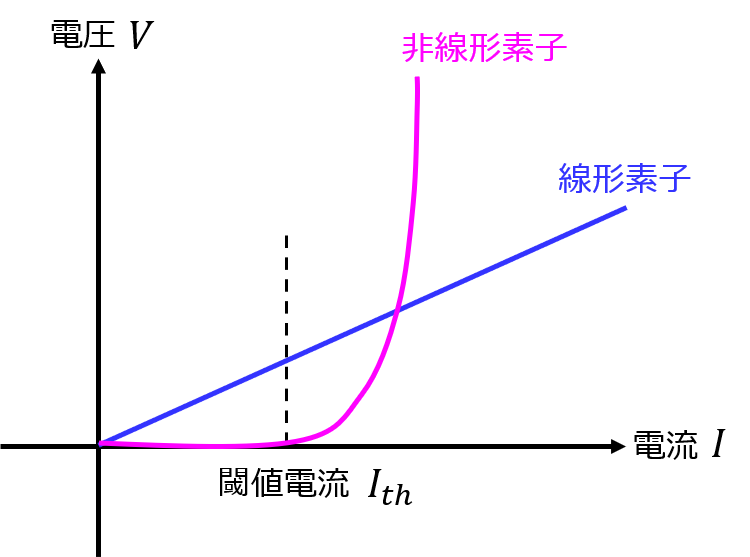
イメージとしては、ダイオードです。ある閾値電流までは殆ど電圧は立ちませんが、閾値を超えると非常に大きな電圧が立ち、これ以上回路に電流が流れないような振る舞いになります。

このような、変数を何乗もした式を手計算でラプラス変換することは非常に厳しく、厳密解を求めることは困難だと考えられます。

このようなとき、計算機を使用して微分方程式をt領域のまま近似解を求める方法があり、オイラー法が最もオーソドックスな解法になります。

本記事では、オイラー法の使い方を、電気回路の過渡現象を題材に考えたいと思います。

そして、発展版として、電気回路で発生したジュール熱を次回の時間ステップで抵抗値にフィードバックする「連成解析」の手法についても説明します。

オイラー法とは

下記の１～３一連の流れを言います。

イメージ論ですが、ある微分方程式の解(真値)は下記のグラフ(桃色)になるとします。

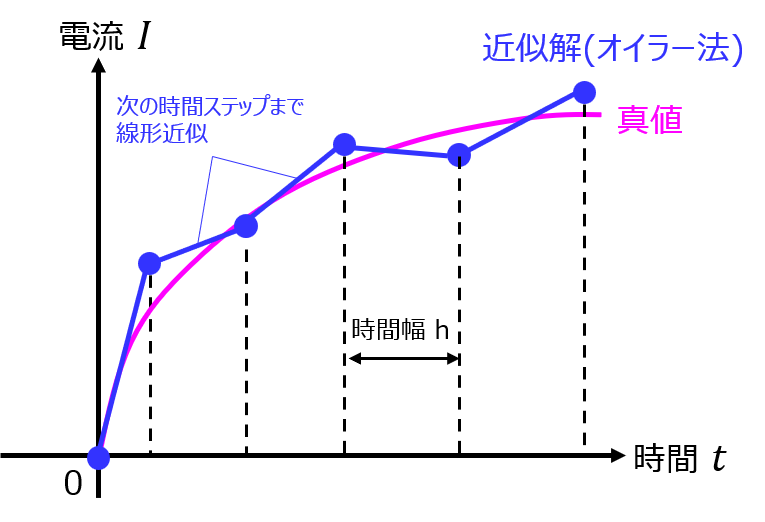
オイラー法で求める近似解は青色のようになります。t=0で求めた傾きを時間幅分掛け算し、その次の時間でも同様のことを行うと、真値に近い離散的な値を得られることを示しています。(線形近似とも言われることがあります。)

オイラー法を用いた回路方程式の変形

概要を説明しても、実際に計算してみないことにはイメージを掴めないと思います。

問題文で与えられた回路方程式を、オイラー法を用いて変形してみましょう。

まず、キルヒホッフの電圧則により

$$\begin{array}{}\text{(3)}& E=L{\displaystyle \frac{dI(t)}{dt}}+R_{1}I+{\left({\displaystyle \frac{I(t)}{5}}\right)}^{10}\cdot I(t)\mathrm{・}\mathrm{・}\mathrm{・}(1)\end{array}$$

を立式することができます。問題文で与えられたパラメータを代入し

$$\begin{array}{}\text{(4)}& 10={\displaystyle \frac{dI(t)}{dt}}+1+{\left({\displaystyle \frac{I(t)}{5}}\right)}^{10}+I(t)\mathrm{・}\mathrm{・}\mathrm{・}(2)\end{array}$$

$$\begin{array}{}\text{(5)}& {\displaystyle \frac{dI(t)}{dt}}=10-I(t)-{\left({\displaystyle \frac{I(t)}{5}}\right)}^{10}\cdot I(t)\mathrm{・}\mathrm{・}\mathrm{・}(3)\end{array}$$

となります。ここで、オイラー法の出番です。

まず、適当な初期値を代入します。ここでは、t=0[s]のとき、回路に電流が流れていないことを利用します。

(i)t=0のとき、$I(t)=0$だから、(3)式に値を代入することにより

$$\begin{array}{}\text{(6)}& {\displaystyle \frac{dI(t)}{dt}}=10\end{array}$$

$$\begin{array}{}\text{(7)}& I(0.1)& =& I(0)+{\displaystyle \frac{dI(t)}{dt}}\ast h\text{(8)}& & =& 0+10\ast 0.1\text{(9)}& & =& 1\end{array}$$

(ii)t=0.1のとき、(i)より、$I(t)=1$だから、(3)式に値を代入することにより

$$\begin{array}{}\text{(10)}& {\displaystyle \frac{dI(t)}{dt}}=10-1=9\end{array}$$

$$\begin{array}{}\text{(11)}& I(0.2)=I(0.1)+9\ast 0.1=1.9\end{array}$$

(iii)t=0.2のとき、$I(t)=1.9$だから・・・

以上を繰り返していくと、近似解を求めることができます。

結局、Excelを使用して解いてみると、以下の表(画像)になります。

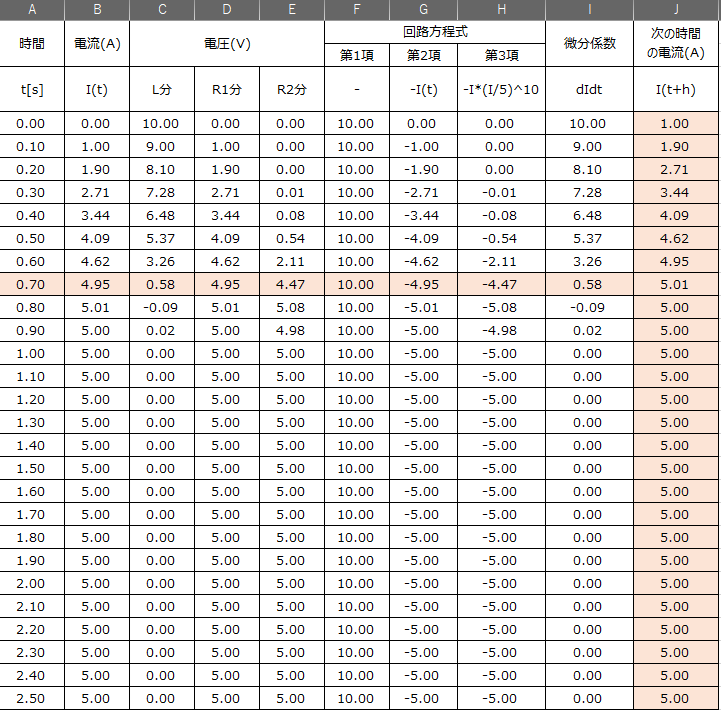
0.7秒あたりで、回路に流れる電流値が5Aに到達し、非線形素子(第3項)から急激に電圧が立つことで電流がこれ以上流れなくなりました。

電流波形をグラフにすると、以下のようになります。

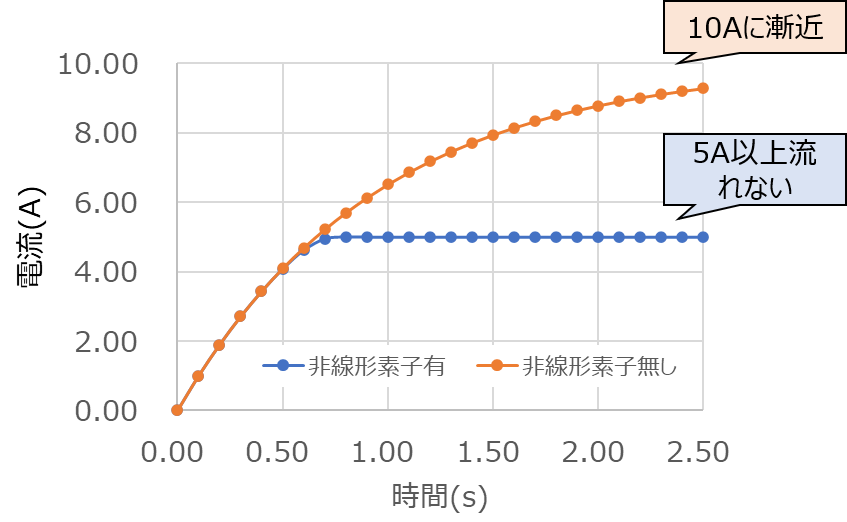
非線形素子が無い場合は10Aへ漸近しますが、有る場合は、先ほどの表のように5A以上流れないことが視覚的にも確認できました。

以上の反復計算を行うことで、非線形項がある微分方程式の場合でも近似解を求めることができます。

発展：電気と熱の連成解析

研究レベルのより発展的な内容になってくると、電流の過渡解析だけ行えば良いものでは無くなってきます。現実的には、抵抗素子に電流が流れるとジュール熱が発生するはずです。

これにより、抵抗素子の温度が上昇し、抵抗値も上昇することが予想されます。

より詳細な解析を行うならば、各時間ステップにおいて抵抗温度値を求め、回路パラメータにフィードバックすることが求められます。

一見、別の領域である2つの世界(本記事では電気と熱)を統合してシミュレーションを行う手法を連成解析と言います。モータなど、電気機器における解析で広く用いられています。

電気と熱の連成解析の手法

まず、ある時間ステップにおいて、電流が流れるとジュール熱$Q[W]$が発生します。これは瞬時値であるため、オイラー法で取っている時間幅$h$をかけると、時間ステップ間で$Qh[J]$の熱エネルギーが発生したことになります。

これを熱伝導方程式に代入することで、抵抗素子の温度上昇を計算することができます。

$$\begin{array}{}\text{(12)}& {\displaystyle \frac{\partial T}{\partial t}}={\displaystyle \frac{{\lambda }_x}{C}}{\displaystyle \frac{{\partial }^{2}T}{\partial x^2}}+{\displaystyle \frac{Qh}{C}}\end{array}$$

※簡単化のため、一次元で考えています。(\lambda_{x}\)は熱伝導率、$C$は熱容量を表します。

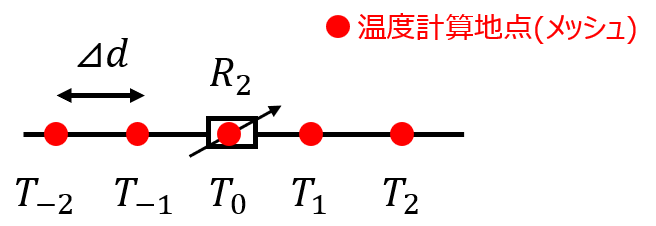
メッシュ間の距離$⊿d$とおく。このとき、中心差分近似により、抵抗$R_2$での温度上昇$T_0(t+1)-T_0(t)$は、以下の式に近似できます。

$$\begin{array}{}\text{(13)}& {\displaystyle \frac{T_0(t+1)-T_0\left(t\right)}{h}}={\displaystyle \frac{{\lambda }_x}{C}}{\displaystyle \frac{T_1\left(t\right)-2T_0\left(t\right)+T_1(t)}{{\left(\mathrm{\Delta }d\right)}^2}}+{\displaystyle \frac{Qh}{C}}\text{(14)}& T_0(t+1)=T_0\left(t\right)+{\displaystyle \frac{{\lambda }_{x}h}{C}}{\displaystyle \frac{T_1\left(t\right)-2T_0\left(t\right)+T_1(t)}{{\left(\mathrm{\Delta }d\right)}^2}}+{\displaystyle \frac{Q{h}^2}{C}}\end{array}$$

で表すことができます。前の時間ステップの値は既知であるため、左辺の未知数を求めることができますね。

ある位置で時間ステップ$h$の間に発生する温度上昇量のイメージは以下になります。

「隣の地点から伝搬する熱量+ある位置で発生するジュール熱に熱容量を割った値」

それぞれ、式(13)の右辺第1項、第2項に対応しています。

次回時間ステップ時、まず電流値の値を求めますが、この時に前回時間ステップで算出した温度を温度に依存する抵抗値の式に代入することで連成解析を実現できます。

境界条件について

メッシュを切っていくと、必ず端点に当たります。ここでの境界条件の取り方で模擬する冷却方法を変化させることができます。

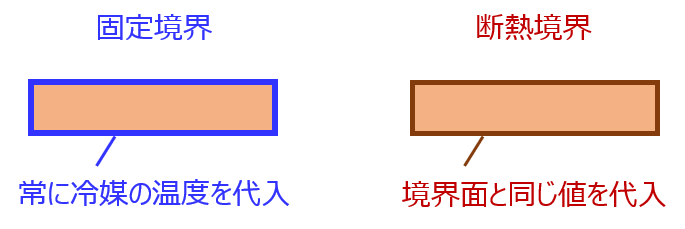
例1)固定境界

冷却性能が高い理想的な冷媒を想定するときに使用します。常に冷媒温度と同じ温度で境界条件を取るため、物体から熱が効率よく出ていきます。

※現実的には、冷媒も温まりますので、固定境界になることはありません。あくまでも理想的な冷却条件です。

例2)断熱境界

端点の温度と同じ温度を取り続けるようにします。このようにすることで、物体から外部への温度勾配が無くなり、物体から熱が出ていかなくなります。これにより、断熱条件を模擬することができます。

その他、液体冷媒を循環する熱交換や、液体冷媒に物体を浸す浸漬冷却という冷却手法もあります。この場合、液体が沸騰し、気泡が発生している間は冷却できません。沸騰曲線を使用し、沸騰の程度を模擬することはできますが、なかなか正確に解析することは難しいです。

個人の能力より、専門シミュレーションソフトにて解析を行った方が時間がかからないかもしれません。

補足

式(13)は前進オイラー法を利用した近似方法です。式から熱伝導を直感的にイメージしやすいですが、あまり広い時間ステップを取ってしまうと発散してしまう欠点があります。

(もっとも、温度は電流に対して変化が遅いので、電流の過渡解析に合わせた時間ステップで温度解析も同期して行えば、発散することはあまり無いです。)

最後に

オイラー法は、感覚的に分かりやすいですが、同時に誤差も大きくなりがちです。

今回は計算収束しましたが、時間ステップが長すぎる場合、誤差が大きくなりすぎて計算が発散することもあります。

このようなときは、時間ステップを短くするなどの対応が必要ですが、今度は計算時間が長くなってしまいます。

このように、数値解析は精度と計算資源の戦いになりがちです。

別の記事で、時間計算量についても論じていく予定ですので、今後ともよろしくお願いいたします。