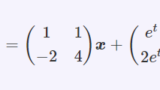数学の科目内容
線形代数、複素関数、微分方程式、ラプラス変換、統計学から構成されています。
本記事では、線形代数~ラプラス変換までの範囲を説明します。
阪大 工学研究科 電気電子情報通信専攻 院試の全体
基礎科目+専門科目で構成されています。
数学は基礎科目に属します。志望コース共通で、9題中5題選択することが必要です。
うち、電気工学コースと、量子情報エレクトリクスは、数学5題中3題、電磁理論+電気回路の4題から2題選択します。
試験時間は180分で、1題当たり45分の配分になります。
- 線形代数 ←本記事で紹介
- 複素関数 ←本記事で紹介
- 微分方程式 ←本記事で紹介
- ラプラス変換 ←本記事で紹介
- 統計学
- 電磁理論(電場)
- 電磁理論(磁場)
- 電気回路
- 電子回路
全体的な難易度ですが、他大学に比べて難しいと思います。全体的な計算量は多く、大問の最後は初見になる問題もあるからです。
後半の電磁理論、電気電子回路の出来にもよりますが、6,7割でも仕方ないと思います。
個人的には、ラプラス変換>線形代数>複素関数>微分方程式の順でオススメします。
ラプラス変換は、電気回路、制御工学で必ず使用する内容ですので、親和性が高いです。積分の求値問題が問われる可能性が高いので、ここを抑えることで満点が狙えます。
線形代数は、出題パターンが絞りやすいので、2番目にオススメしています。
固有値→固有ベクトルは必ず出てきますので、ここで半分取って残りの問題を取れるだけ取る。この方針で、ある程度得点安定が見込めるのではないかと思います。
複素関数と積分は、他大との兼ね合いと思います。
他大でも出題されるならば、相乗効果を狙うという観点で十分オススメできます。最後の問題も、ラプラス変換と似た形式であることが多いので、場合によっては高得点も狙えます。
微分方程式は、他大では出てきづらいので個人的には選択しません。
しかし、オーソドックスな問題が多いため、解き方を知っていれば4分野の中で最も完答しやすい分野と思います。大阪大学に特化して院試対策するならば、選択したいところです。
対策に使える参考書、問題集
全体
最近6か年は以下の分野の出題がありました。
- 2023年:
- 連立方程式が解を持つ行列の条件。任意の自然数iに対する固有値、固有ベクトル
- ガウス積分とβ関数
- 複素積分の実数条件、極限
- 連立微分方程式をラプラス変換を利用して解く問題
- 2022年:
- ジョルダン標準形を用いた準対角化
- 変数変換を用いた2階線形微分方程式の一般解
- 複素関数(正則)の性質
- フーリエ変換を用いた積分の求値問題
- 2021年:
- 漸化式の行列表示。ジョルダン標準形による準対角化
- 正則関数とコーシーリーマンの式
- フーリエ変換と信号の図示
- ラプラス変換と無限級数
- 2020年:
- 行列のn乗計算
- オイラー型微分方程式
- 複素積分を用いた積分の求値問題
- フーリエ変換と常微分方程式の計算
- 2019年:
- 行列指数関数の計算。曲線の図示
- 微分方程式の変数変換を利用した積分の求値問題
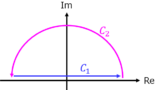
- 複素積分を用いた積分の求値問題
- ラプラス変換を用いた微分方程式の計算
- 2018年:
- 転置行列の対角化を用いた固有値の計算
- 多項式関数の微分方程式
- ジョルダン補助定理を用いた複素積分
- ラプラス変換を用いた微分方程式の解
2023年は傾向からずれましたが、行列は対角化が多いです。他、誘導に従って積分値を求める問題が多いです。
微分方程式が出題されない年度もありますが、ラプラス変換などで融合問題が出題されることがあります。
幅広く、深い勉強が必要です。
線形代数
連立1次方程式から学ぶ線形代数 佐藤信哉 (著)
阪大の指定教科書です。線形代数に限らずですが、市販の数学の参考書は充実しています。こちらを購入されなくとも、自身のお持ちの教科書で勉強でも問題無いと思います。専願で行くならば、購入すると良いです。
複素関数、微分方程式、ラプラス変換
一纏めにし申し訳ありませんが、とてもオススメできる本があります。
阪大のシラバスで紹介されている参考書です。こちらの本で紹介されている内容が多数院試で出題されますので、阪大を受けるならば是非とも購入した方が良いです。
他、工学系の数学で使用する分野の基本事項がまとまっています。筆者としても他大学の院試の解答を作成するときに、よく見返します。
欠点としては、演習問題の解答が略解しか無いことです。非常に痛いですが、例題に対する解答は記載されています。同じ考え方で演習問題も解けることが多いので、院試勉強として間を埋め合わせる練習と考えて解くしかないです。
一応、下記の記事で重要と思われる問題(略解しか無い)の解説を行っています。よろしければご覧ください。
阪大院試に太刀打ちするためには、難しめの内容を解く必要があります。中級者以上の参考書紹介となりました。
基本事項から学びなおしたい場合は、市販で販売されているマセマ、講義ノートなどを活用することをオススメします。
問題集
他の記事でも触れていますが、阪大対策においても下記がオススメです。
詳解と演習大学院入試問題 海老原 円 (著), 太田 雅人 (著)
最近の傾向に即した院試問題を事細かに解説しています。全分野カバーしています。難しい問題もありますが、A問題から順に解いていくことでステップアップできると思います。
阪大対策の場合は、できればB問題まで目を通したいです。しかし、全部解く必要は無く、類題と判断した問題だけ勉強すると良いです。
対策に使える他大学の問題
難しめの問題を出題する大学に注目します。
- 線形代数:東工大(情報通信系)、名大、東北大(2020年以前)
- 複素関数:東工大(電気電子系)、京大(通信情報)
- 微分方程式:東工大(電気電子系)、京大、神戸大
- ラプラス変換:該当なし
基本的に、東工大がレベル的に近しいです。専攻によって、出題する/しない分野が分かれていますが、分野ごとにチェック下さればと思います。情報工学系の問題についてもチェックすると良いです。
一方で、ラプラス変換の問題については、なかなか出題大学が見当たりません。東北大からたまに出題ありますが、レベル的に違いすぎます。
市販の問題集で演習することが結局良いです。
下記の記事でも阪大頻出問題を解説しているので、よろしければご確認ください。
最後に
数学は、5題中3題の選択となっています。どれか一つでもヤマを外してしまうと、大幅ビハインドになってしまいます。保険1科目を追加し、4題体制での受験をオススメします。