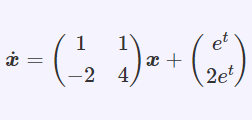以下の\(\dot{\boldsymbol{x}}=\boldsymbol{Ax}+\boldsymbol{b}\) 型 1階線形連立微分方程式を解け。\begin{eqnarray}\dot{\boldsymbol{x}}= \begin{pmatrix} 1 & 1 \\ -2 & 4 \end{pmatrix}\boldsymbol{x}+\begin{pmatrix} e^{t} \\ 2e^{t} \end{pmatrix}\end{eqnarray}
工学系の数学解析 大阪大学出版会 P205 4.(1) より引用
はじめに
こちらの問題、すぐに解き終わると思いきや一癖あります。
仮に、\(\boldsymbol{b}=\begin{pmatrix} e^{t} \\ 2e^{t} \end{pmatrix}\)の項が0ならば、\(\dot{\boldsymbol{x}}=\boldsymbol{Ax}\)型になります。
この時は、以下の手順で比較的楽に解を求めることができます。
- \(\boldsymbol{A}\)の固有値\(\lambda=\lambda_{1},\lambda_{2}\)を求める
- \(\lambda=\lambda_{1},\lambda_{2}\)の固有ベクトル\(\boldsymbol{p_{1}},\boldsymbol{p_{2}}\)を求める
- \(\boldsymbol{x}=C_{1}\boldsymbol{p_{1}}e^{\lambda_{1}t}+C_{2}\boldsymbol{p_{2}}e^{\lambda _{2}t}\)で一般解\(\boldsymbol{x}\)を得る。
しかし、本問はこれだけでは終わりません。
\(\boldsymbol{b}\)の条件が残っているので解になっていません。
そして、ネットを見ていると解説サイトも少ないように感じます。
そこで、本記事では、\(\boldsymbol{b}\)項が付いた微分方程式に対して、どのように解を求めていくか、概要を解説していきたいと思います。
問題は引用元の参考書から抜粋しましたが、答えは略解しか無かったため、途中過程の埋め合わせができればと思います。
本記事で覚えたい解き方
本問は、以下の手順で解くことができます。
- \(\boldsymbol{A}\)の固有ベクトル\(\boldsymbol{p_{1}},\boldsymbol{p_{2}}\)を求める
- 行列\(\boldsymbol{P}\)=\((e^{\lambda_{1}t}\boldsymbol{p_{1}},e^{\lambda_{2}t}\boldsymbol{p_{2}})\)の逆行列\(\boldsymbol{P^{-1}}\)を求める。
- \(\boldsymbol{P^{-1}b}\)を計算し、結果を積分。\(\boldsymbol{Q}\)とする。
- \(\boldsymbol{x}=\boldsymbol{PQ}\)より、一般解\(\boldsymbol{x}\)が求まる。
ただし、\(\boldsymbol{p_{1}},\boldsymbol{p_{2}}\)は線形独立であることが条件です。
上記の解の求め方は、定数変化法に基づいているようです。定数変化法の詳しい説明については、別サイトをご覧ください。(1変数微分方程式の場合ならば、説明しているサイト様が他にいらっしゃるはず。)
上記の手順が文字ばかりの説明になってしまい、恐縮です。
まずは、下記に解答例を記載しますので、それを一読した後こちらに戻ってくると理解が進むかもしれません。
解答例
まず、\(\begin{pmatrix} 1 & 1 \\ -2 & 4 \end{pmatrix}\)の固有値を求める。
\begin{eqnarray}\begin{vmatrix} 1-\lambda & 1 \\ -2 & 4-\lambda \end{vmatrix}&=&(1-\lambda)(4-\lambda)+2 \\ &=&\lambda^{2}-5\lambda+6 \\ &=&(\lambda-2)(\lambda-3)=0\end{eqnarray}
\(\lambda_{1}=2,\lambda_{2}=3\)だから、それぞれの固有ベクトルは
(i)\(\lambda_{1}=2\)のとき、\(x_{1}=x_{2}\)だから、\(\boldsymbol{p_{1}}=\begin{pmatrix} 1 \\ 1 \end{pmatrix}\)
(ii)\(\lambda_{2}=3\)のとき、\(x_{1}=2x_{2}\)だから、\(\boldsymbol{p_{2}}=\begin{pmatrix} 1 \\ 2 \end{pmatrix}\)
よって、\(\boldsymbol{P}\)=\((\boldsymbol{p_{1}},\boldsymbol{p_{2}})=\begin{pmatrix} e^{2t} & e^{3t} \\ e^{2t} & 2 e^{3t} \end{pmatrix}\)で表すことができる。
これの逆行列は、\begin{eqnarray}\boldsymbol{P^{-1}}&=&\dfrac{1}{3e^{5t}-2e^{5t}}\begin{pmatrix} 2e^{3t} & -e^{3t} \\ -e^{2t} & e^{2t} \end{pmatrix}\\ &=& \begin{pmatrix} 2e^{-2t} & -e^{-2t} \\ -e^{-3t} & e^{-3t} \end{pmatrix}\end{eqnarray}だから、\(\boldsymbol{b}=\begin{pmatrix} e^{t} \\ 2e^{t}\end{pmatrix}\)と掛け合わせることにより
\begin{eqnarray}\boldsymbol{P^{-1}b}&=&\begin{pmatrix} 2e^{-2t} & -e^{-2t} \\ -e^{-3t} & e^{-3t} \end{pmatrix}\begin{pmatrix} e^{t} \\ 2e^{t}\end{pmatrix} \\ &=&\begin{pmatrix} 0 \\ e^{-2t}\end{pmatrix}\end{eqnarray}
これを積分することで、
\begin{eqnarray}\boldsymbol{Q}=\begin{pmatrix} C_{1} \\ -\dfrac{1}{2}e^{-2t}+C_{2}\end{pmatrix}\end{eqnarray}
を得る。(ただし、\(C_{1}、C_{2}\)は任意の定数)
求める解\(\boldsymbol{x}\)は、\(\boldsymbol{x}=\boldsymbol{PQ}\)より
\begin{eqnarray}\begin{pmatrix} x_{1} \\ x_{2} \end{pmatrix}&=&\begin{pmatrix} e^{2t} & e^{2t} \\ e^{3t} & 2 e^{3t} \end{pmatrix}\begin{pmatrix} C_{1} \\ -\dfrac{1}{2}e^{-2t}+C_{2}\end{pmatrix}\\ &=&\begin{pmatrix} C_{1}e^{2t}+C_{2}e^{3t}-\dfrac{1}{2}e^{t} \\ C_{1}e^{2t}+2C_{2}e^{3t}-e^{t}\end{pmatrix}\end{eqnarray}
最後に
本問のような微分方程式は、制御工学(現代制御)の状態方程式と同じ型になっています。解き方を覚えておくと、現代制御で同様の問題が出題された時の助けになるかもしれません。
参考文献
工学系の数学解析 大阪大学出版会 八木 厚志(著) 森田 浩(著) P203