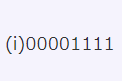2進表現について、以下の問に答えよ。
(1) (i)+78 (ii)-66 を8bitの2進数表記でそれぞれ表せ
(2)下記の2の補数表現の8bitの情報を絶対値表記に変換せよ。
(i)00001111 (ii)11110000
(3)下記の8bitの2の補数表現の2進数体系での加算及び減算結果を示せ。オーバーフローする際は、その旨記載すること。
(i)11001100+10101010 (ii)10101011-10101100
京都大学大学院 情報学研究科 通信情報システム専攻 平成27年入試問題 A-8 より 抜粋 (3)の問題文(オーバーフロー部分)を追記
はじめに
2進数の計算は、殆どの大学の計算機工学の講義にて最初に扱われる内容です。他の科目でも扱われることが多く、親しみやすい内容のはずです。
しかし、当たり前のように触れてしまうために、少し細かいことを問われた際、ド忘れしてしまうかもしれません。
実際、京大に限らず院試で出題する大学は他にあります。
本記事では、2進数の計算を試験問題として問われた際に私が行っている解き方を説明します。
テクニカルなことはせず、基本に忠実に解くことにしています。解き方に癖が無いため、忘れにくいと思います。
10進数➡2の補数表記
似たような解き方はいくつかありますが、本サイトでは下記のやり方をオススメしています。
- 変換元の10進数(絶対値)から、2の累乗で表せる数の最大値を0になるまで引いていく。
- 0になったとき、今まで引いてきた2の累乗に対応するbitに1を立てる。
- 変換元の10進数が負の場合、bit反転し、最下位bitに1を足す。
一番最初の手順を覚えて置き、2の補数表現の知識さえあれば、作業で解くことができます。
負の数のまま考える方法もあるかもしれませんが、正にして考えた方がミスが少ないと考えています。後から負に直せば良いと思います。
このように、負の数を正として変換して計算する方針は、(3)でも同様に使用しています。
解答例
(i)+78について
\begin{array}{rr} & 78\\-\big{)}&64\\\hline&14\\-\big{)}&8\\\hline&6\\-\big{)}&4\\\hline&2\\-\big{)}&2\\\hline&0\end{array}
\(64→2^{6}、8→2^{3}、4→2^{2}、2→2^{1}\)のため、\(2^{0}~2^{7}\)までの8bitのうち、1,2,3,6bit目に1が立ちます。
よって、\(+78→(01001110)_{2}\)
(ii)-66について、まず+66の2進数表記を考えて
\begin{array}{rr} & 66\\-\big{)}&64\\\hline&2\\-\big{)}&2\\\hline&0\end{array}
\(64→2^{6}、2→2^{1}\)のため、1bit目と6bit目に1が立つ。
よって、\(+66→(01000010)_{2}\)である。これをbit反転し、最下位bitに1を足すと2の補数になる。
\(-66→(10111101)_{2}+(00000001)_{2}=(10111110)_{2}\)
2の補数➡絶対値表記
絶対値表記は、所属する大学次第では、講義での取り扱いが無いかもしれません。
ですが、下記のルールさえ覚えられれば、特に怖いものでは無いはずです。
絶対値表記のルール
最上位bitを符号として表す。0~最上位bitの一つ下までは通常の2進数→10進数変換の演算と同じ
正だと最上位bitは0、負だと1になります。
例えば、0001は、1です。1001は、-1です。
2の補数の場合は、最上位bitに1が立てば、\(-2^{最上位bit-1}\)の数値が入っている扱いになります。しかし、絶対値表記は違います。
純粋に、最上位bitより下のbit分の数値を足していき、最後に符号を確認すれば良いのです。
解答例
(i)2の補数\((00001111)_{2}\)を10進数に変換すると、1+2+4+8=15
元々の数値は正であるので、絶対値表記も変わらない。
よって、2の補数\((00001111)_{2}\)の絶対値表記は、\((00001111)_{2}\)
(ii)2の補数\((11110000)_{2}\)を10進数に変換すると、-128+64+32+16=-16
-16を絶対値表記に直すとき、8bit目に1を立て、(最上位-1)=7bit目から16を表すことを考える。
\(16→2^{4}\)のため、4bit目に1が立つ。
以上より、2の補数\((11110000)_{2}\)の絶対値表記は、\((10010000)_{2}\)
結局、負の場合だけ表記方法が2の補数表現と異なります。
2の補数表記の筆算
最後に、2の補数表記の筆算です。
前章で紹介した絶対値表記は、いつも10進数を取り扱っている私たちにとって感覚的に分かりやすい表記になっています。
これだけ見ると、計算機工学の世界では絶対値表記で計算することがスタンダードになってもおかしくないはずです。
しかし、実際は2の補数での計算が主流になっています。
この理由が本問で分かります。結論、筆算をするときに役立ちます。
例えば、2-3=-1を、絶対値表記と2の補数表現それぞれで計算してみましょう。
絶対値表記の筆算
簡単化のため、3bitで考えます。
\(2→(010)_{2}、-3→(111)_{2}\)なので
\begin{array}{rr} & 010\\+\big{)}&111\\\hline&(1)001\end{array}
-1になるはずが、結果は1になってしまいました。桁の繰上りも踏まえて4bitで符号を区別するなら-1になりますが、足す前から4bit目で符号を区別しないとつじつまが合いません。
このように、単純な計算では結果を合わせることが出来ず、どちらの数字の方が大きいか、人間の目で区別してから計算する必要があります。
工夫すれば2-3の順序のまま解くことが出来るかもしれませんが、やはりひと手間必要です。
2の補数の筆算
\(2→(010)_{2}、-3→(101)_{2}\)なので
\begin{array}{rr} & 010\\+\big{)}&101\\\hline&111\end{array}
2の補数表現の\((111)_{2}→-1\)のため、単純な筆算で答えが合いました。
このように、2の補数を使用すると、単純に筆算をするだけで答えを導くことができます。
以上が2の補数を使用するメリットです。
ただし、今回の問:8bitの2進数表記 → -128~127の範囲外の計算結果になる場合は注意が必要です。
そもそも、8bitで表すことができる数の範囲を超えてしまっているので、絶対値表記、2の補数表記問わず正しい答えを導けないです。
解答例
(i)11001100+10101010 (10進数:-52-86=-138)
\begin{array}{rr} & 11001100\\+\big{)}&10101010\\\hline&(1)01110110\end{array}
\((01110110)_{2}→118\)となってしまい、正しい答え-138を導けませんでした。オーバーフローです。
(ii)10101011-10101100 (10進数:-85+84=-1)
まず、引き算にかかっている\((10101100)_{2}\)を、+の演算ができるよう変換します。
2の補数を取ればよいので、\((01010011)_{2}+(00000001)_{2}=(01010100)_{2}\)なので
\begin{array}{rr} & 10101011\\+\big{)}&01010100\\\hline&11111111\end{array}
正しい答え(-1)を算出できました。
このように、同じ符号同士の計算ならばオーバーフローするリスクがありますが、異符号同士の場合はオーバーフローしないことが分かります。
検算する際にこちらの知識は役立つかもしれません。
最後に
本問は、万人が覚えること少なく解けることを重視しました。その分、解説が抽象的で、語弊のある内容が含まれているかもしれません。
管理人からのお願いとして、市販の問題集で演習を積むなどし、自分なりの理解を深めていただきたいです。
また、意気揚々と院試問題を解説しましたが、間違いある場合は申し訳ございません。お問い合わせフォームでご指摘下さると幸いです。
参考文献
ディジタル回路基本演習 石坂陽之助(著) 第1章