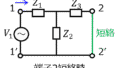
下記の2端子対回路のz行列を求めよ。
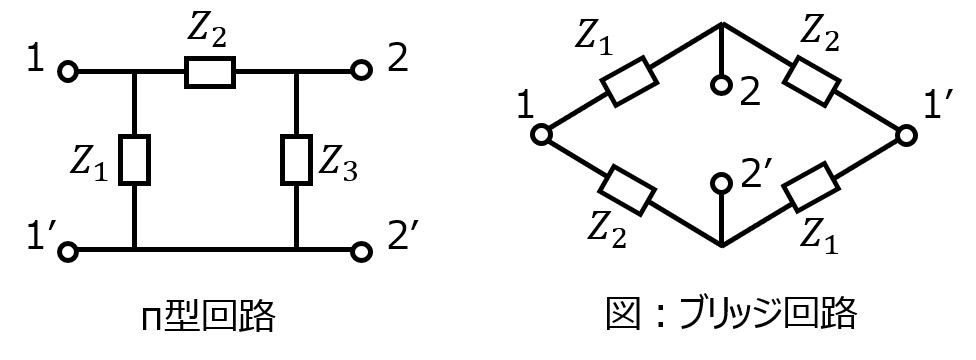
(1)π型回路
(2)インピーダンスが\(Z_{1},Z_{2}\)で表されるブリッジ回路
(3)(2)のブリッジ回路を2つ直列接続した回路
Z行列とは
2端子対回路における入力端および出力端の電圧\(V_{1},V_{2}\)の関係をインピーダンス行列で表したものになります。入力端から流れる電流\(I_{1}\)、出力端から流れる電流\(I_{2}\)を変数とし、z行列を
\begin{pmatrix} z_{11} & z_{12} \\ z_{21} & z_{22}\end{pmatrix}
とすると、2端子対回路は下記の式で表されます。
\begin{aligned}\begin{pmatrix} V_{1} \\ V_{2} \end{pmatrix}=\begin{pmatrix} z_{11} & z_{12} \\ z_{21} & z_{22}\end{pmatrix}\begin{pmatrix} I_{1} \\ I_{2} \end{pmatrix}\end{aligned}
なお、回路の双対性により\(z_{12}=z_{21}\)が成立します。
Z行列の求め方
- 端子2を開放\(I_{2}=0\)し、端子1に電圧源\(V_{1}\)を接続したときに回路に流れる電流\(I_{1},I_{2}\)の関係式を求める。
- 端子1を開放\(I_{1}=0\)し、端子2に電圧源\(V_{1}\)を接続したときに回路に流れる電流\(I_{1},I_{2}\)の関係式を求める。
- 1.2.で求めた関係式を用い、z行列の具体的な値を求める。
教科書では、いちいち開放した図で回路を書きなおし、説明していないことが多いです。しかし、暗黙の了解ですので、実際は一方の端子を開放した前提で関係式を立てています。初学者の場合、何かと誤解しがちな内容ですが、まずは上記の手順をマスターすることが慣れへの近道です。
また、Z行列では端子2に流れる電流の向きは回路に向かって流れる側を正と置きます。F行列とは反対なのでご注意下さい。
例題
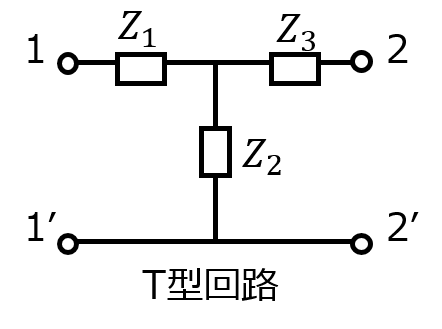
端子1-2の間にインピーダンス\(Z_{1},Z_{2},Z_{3}\)がT型に接続されている場合を考えます。
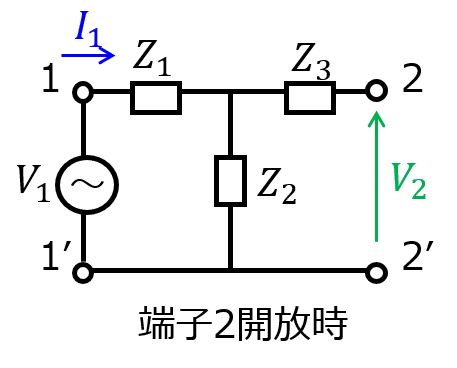
まずは手順1:端子2を開放したときを考えます。\(I_{2}=0\)で、\(Z_{3}\)に電流は流れないことから
\begin{aligned}V_{1}=Z_{1}I_{1}+Z_{2}I_{1} \\ V_{2}=Z_{2}I_{1}\end{aligned}
(2)式と比較すると\(z_{11}=Z_{1}+Z_{2},z_{12}=Z_{2}\)が分かる。
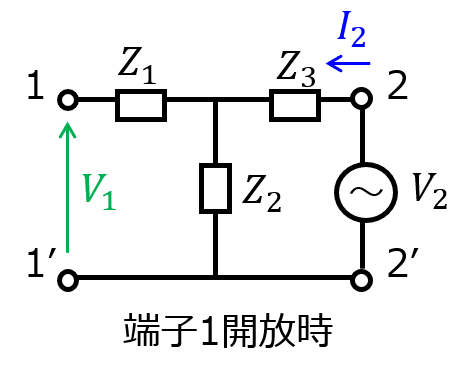
次に、手順2:端子1を開放したときを考えます。回路の対称性により
\begin{aligned}V_{2}=Z_{2}I_{2}+Z_{3}I_{2} \\ V_{2}=Z_{2}I_{2}\end{aligned}
(2)式と比較すると\(z_{21}=Z_{2},z_{22}=Z_{2}+Z_{3}\)が分かる。
以上より、求めるz行列は
\begin{pmatrix} Z_{1}+Z_{2} & Z_{2} \\ Z_{2} & Z_{2}+Z_{3}\end{pmatrix}
Z行列の性質
以下を覚えておくと、問題を解くうえで有利になります。
- 回路の対称性により、\(z_{12}=z_{21}\)
- Z行列\(\boldsymbol{Z_{1}},\boldsymbol{Z_{2}}\)でそれぞれ示される2端子対回路を直列接続した回路におけるZ行列は\(\boldsymbol{Z_{1}+Z_{2}}\)
1.について、例題を読んでいて気付いた方も居るかもしれません。端子1-1’を開放した時、端子2-2’を開放した時、それぞれから見て回路中央部分のインピーダンスは変わらないことから上記の関係式が成立します。
2.について、そもそもz行列(特に\(z_{11}\)成分)の意味として、”出力端を開放したときの入力インピーダンス”になります。となると、入力端と出力端の間に複数の素子が入り、それぞれのZ行列で表されるとすると、入力インピーダンスの観点で言えば足し合わせるだけで全体のZ行列の表現が可能だと直感的に分かります。
補足:2端子対回路の定義
何の気なしに使っている2端子対回路という言葉ですが、実際どのような条件を満たせばそう呼べるのでしょうか。結論ですが、下記3点が成立するときになります。
- 回路に非線形素子が含まれておらず、重ね合わせの理が成立すること
- 端子1から流れ出る電流、端子1’に入る電流が等しいこと(端子2-2’も同様)
- 内部に発振回路を持たないこと
試験で問われることは少ないですが、教養として持っておくと吉です。”内部の素子が線形素子で構成されて、発振しないこと”と大まかに覚えておくと大丈夫です。
解答例
例題と同様の手順で解いていきます。
(1)π型回路
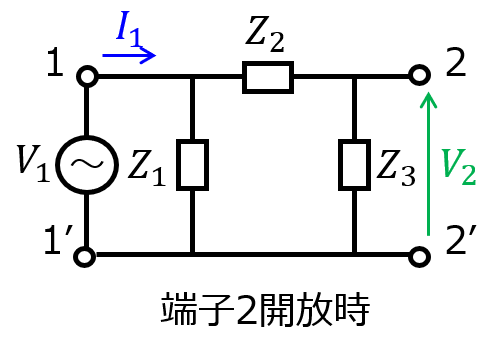
まず、端子2-2’を開放したときの端子1-1’間の電圧\(V_{1}\)を考える。\(Z_{1}\)と\(Z_{2},Z_{3}\)の並列回路と見られるので
\begin{aligned}V_{1}&=\dfrac{Z_{1}(Z_{2}+Z_{3})}{Z_{1}+Z_{2}+Z_{3}}I_{1}\end{aligned}
これが\(z_{11}\)成分にあたる。
また、\(I_{1}’=\frac{Z_{1}}{Z_{1}+Z_{2}+Z_{3}}\)だから
\begin{aligned}V_{2}&=Z_{3}I_{1}’ \\ &=\dfrac{Z_{1}Z_{3}}{Z_{1}+Z_{2}+Z_{3}}\end{aligned}
これが\(z_{12}=z_{21}\)成分にあたる。
以上より、求めるZ行列は
\begin{aligned}\boldsymbol{Z_{1}}=\begin{pmatrix}\dfrac{Z_{1}(Z_{2}+Z_{3})}{Z_{1}+Z_{2}+Z_{3}} & \dfrac{Z_{1}Z_{3}}{Z_{1}+Z_{2}+Z_{3}} \\ \dfrac{Z_{1}Z_{3}}{Z_{1}+Z_{2}+Z_{3}} & \dfrac{Z_{3}(Z_{1}+Z_{2})}{Z_{1}+Z_{2}+Z_{3}}\end{pmatrix}\end{aligned}
(2)ブリッジ回路
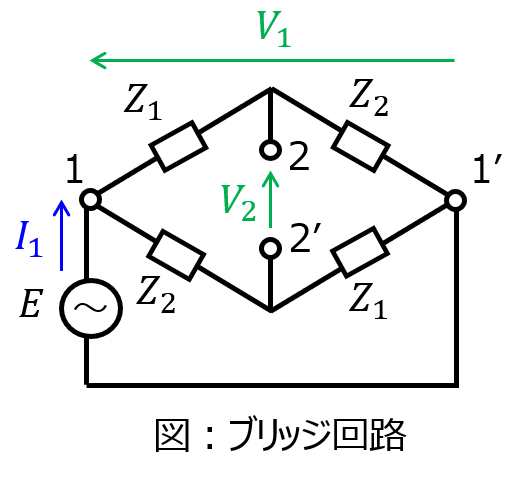
端子2-2’を開放したとき、回路はインピーダンス\(Z_{1}+Z_{2}\)の並列回路である。電流\(I_{1}\)は半分ずつ分流するので
\begin{aligned}V_{1}=\dfrac{Z_{1}+Z_{2}}{2}I_{1}\end{aligned}
\begin{aligned}V_{2}=Z_{2}\dfrac{I_{1}}{2}-Z_{1}\dfrac{I_{1}}{2}\end{aligned}
それぞれ、\(z_{11},z_{21}\)成分に対応する。
端子1-1’を開放したとき、回路の対称性から
\begin{aligned}V_{1}=\dfrac{Z_{2}-Z_{1}}{2}I_{1}\end{aligned}
\begin{aligned}V_{2}=\dfrac{Z_{1}+Z_{2}}{2}I_{2}\end{aligned}
それぞれ、\(z_{12},z_{22}\)成分に対応する。
以上より、求めるz行列は
\begin{aligned}\boldsymbol{Z_{2}}=\begin{pmatrix}\dfrac{Z_{1}+Z_{2}}{2} & \dfrac{Z_{2}-Z_{1}}{2} \\ \dfrac{Z_{2}-Z_{1}}{2} & \dfrac{Z_{1}+Z_{2}}{2}\end{pmatrix}\end{aligned}
(3)ブリッジ回路の直列接続
Z行列の性質2より、(2)の結果を2回足し合わせれば良い。
\begin{aligned}\boldsymbol{Z_{3}}&=\boldsymbol{Z_{2}}+\boldsymbol{Z_{2}} \\ &=\begin{pmatrix}Z_{1}+Z_{2} & Z_{2}-Z_{1} \\ Z_{2}-Z_{1} & Z_{1}+Z_{2}\end{pmatrix}\end{aligned}
最後に
これくらいの問題が解けるようになれば、院試でもそこそこ得点できるようになるはずです。