【IIRフィルタ】z変換を用いた安定性の判別方法

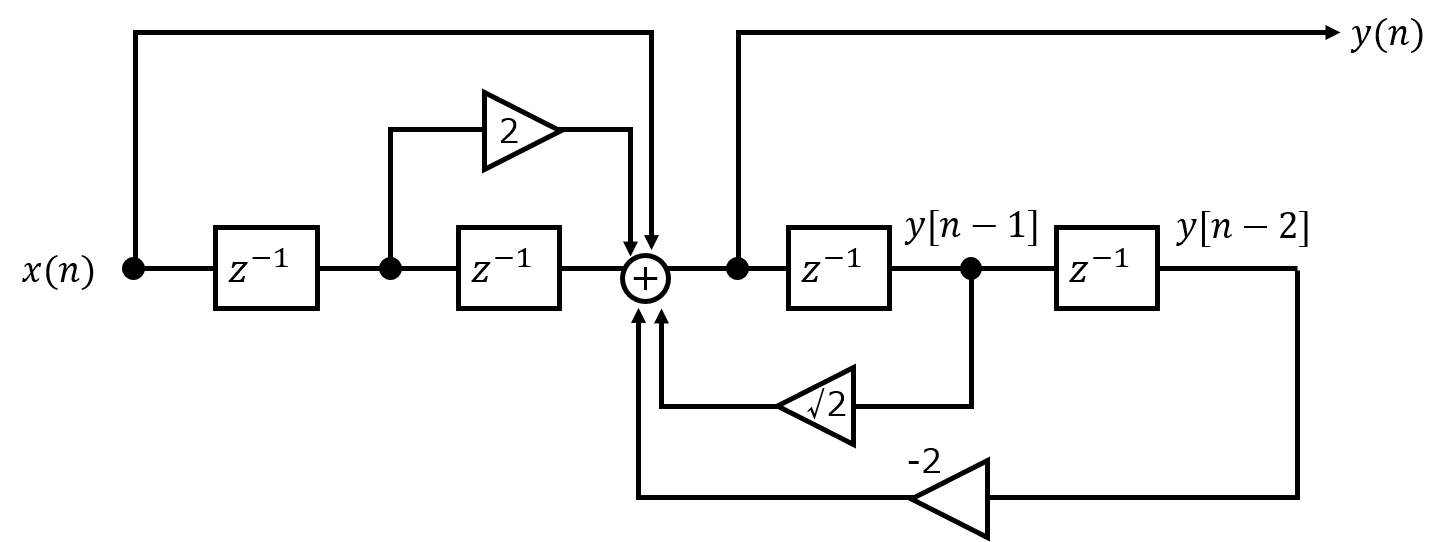
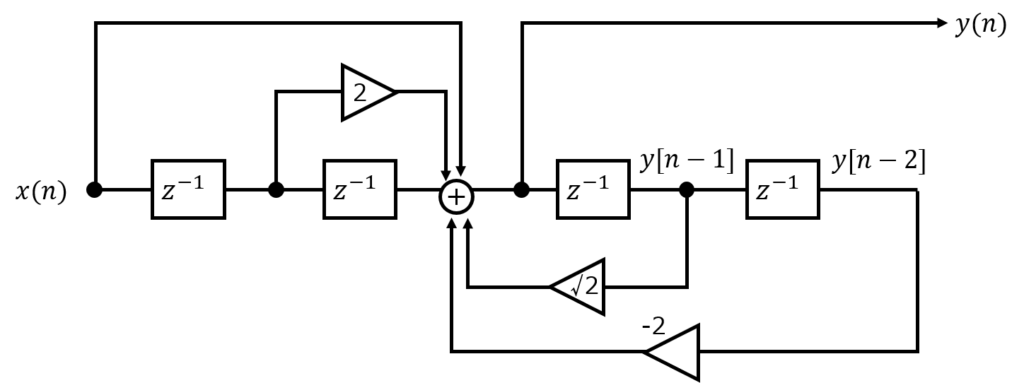
【問】以下のシステムで表される2次IIRフィルタについて、安定性を判別せよ。

はじめに
本問で覚えたいこと
解答例
補足
最後に
参考文献

はじめに

本問は、比較的オーソドックスな問題と思います。問題集で類題を見ている方も多いのではないでしょうか。

与えられた差分方程式から伝達関数を求め、その安定性を判別する問題解説はネットで扱われていました。しかし、システム図から差分方程式を作成する過程までは無かったので、今回扱うことにしました。制御工学で安定性判別をしている方々ならば、それに通ずる内容もあり、とっつきやすい内容ではないかと思います。

本問で覚えたいこと

システム図から差分方程式[n]を立式する。
差分方程式をz変換し、伝達関数\(H(z)\)を求める。
伝達関数の極を求め、絶対値が1より大きいか確認する。

制御工学と解答パターンは似ています。

伝達関数がs平面ではなくz平面であること。差分方程式の項が[n-1]であれば\(z^{-1}\)、[n-2]ならば\(z^{-2}\)がz変換後に付くこと、安定性判別を単位円で行うことが信号処理ならではの内容です。

IIRフィルタとは

入力\(x\)にインパルス入力を与えた時、出力\(y\)の応答が無限に続くことを言います。

問題で与えられたフィルタ回路は、加算器+に対し出力yのフィードバック要素が加算されています。

このように、フィードバックループがある場合は、IIRフィルタになりやすいです。

逆に、フィードフォワードのように、入力から出力までの信号の流れが一本道=フィードバックループが無い場合は、応答が有限時間で0になります。

このような回路をFIRフィルタと言います。

解答例

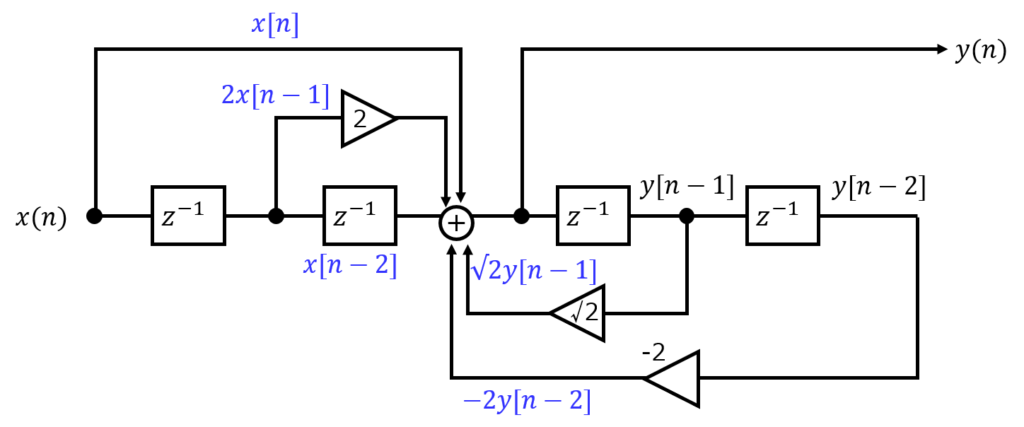
システム図を読み解き差分方程式を作成する。遅延素子\(z^{-1}\)1つにつき、信号が1ステップ分遅れるから

\begin{eqnarray}y\left( n\right) =\sqrt{2}y\left( n-1\right) -2y\left( n-2\right) +x\left( n\right) +2x\left( n-1\right) +x\left( n-2\right) \end{eqnarray}

で得られる。これをz変換し、

\begin{align}Y\left( z\right) &=\sqrt{2}Y\left( z\right) z^{-1}-2Y\left( z\right) z^{-2}+X\left( z\right) +2x\left( z\right) z^{-1}+x\left( z\right) z^{-2} \\ \left( 1-\sqrt{2}z^{-1}+2z^{2}\right) Y\left( z\right) &=\left( 1+2z^{-1}+z^{-2}\right) X\left( s\right) \\ H\left( z\right) &=\dfrac{1+2z^{-1}+z^{-2}}{1-\sqrt{2}z^{-1}+2z^{-2}} \end{align}

極=0を考える。

\(z=\dfrac{-\sqrt{2}\pm i\sqrt{6}}{2}\)になる。

極の絶対値は、\(\sqrt{\left( \dfrac{\sqrt{2}}{2}\right) ^{2}+\left( \dfrac{\sqrt{6}}{2}\right) ^{2}}=2\)

1より大きいため不安定になる。