生起確率\(P(0)=0.9,P(1)=0.1\)の2元情報源\(s_{1}\)がある。以下の問に答えよ。
なお、\(\log_{2}0.9=-0.15,\log_{2}0.1=3.3\)を用いて良い。
(1)\(s_{1}\)の情報量とエントロピーを求めよ。
(2)3次の拡大情報源\(s^{3}\)のエントロピー\(H_{s^{3}}\)を求めよ。
4つの記号\(S_{0},S_{1},S_{2},S_{3}\)の情報源がある。発生確率がそれぞれ\(p_{0},p_{1},p_{2},p_{3}\)とする。発生確率が
\begin{aligned}p_{0}+p_{1}+p_{2}+p_{3}=1\end{aligned}
とするとき、情報源のエントロピー\begin{aligned}H(S)=-p_{0}\log_{2}p_{0}-p_{1}\log_{2}p_{1}-p_{2}\log_{2}p_{2}-p_{3}\log_{2}p_{3}\end{aligned}を最大化する確率\(p_{0},p_{1},p_{2},p_{3}\)を求めよ。
情報量とは
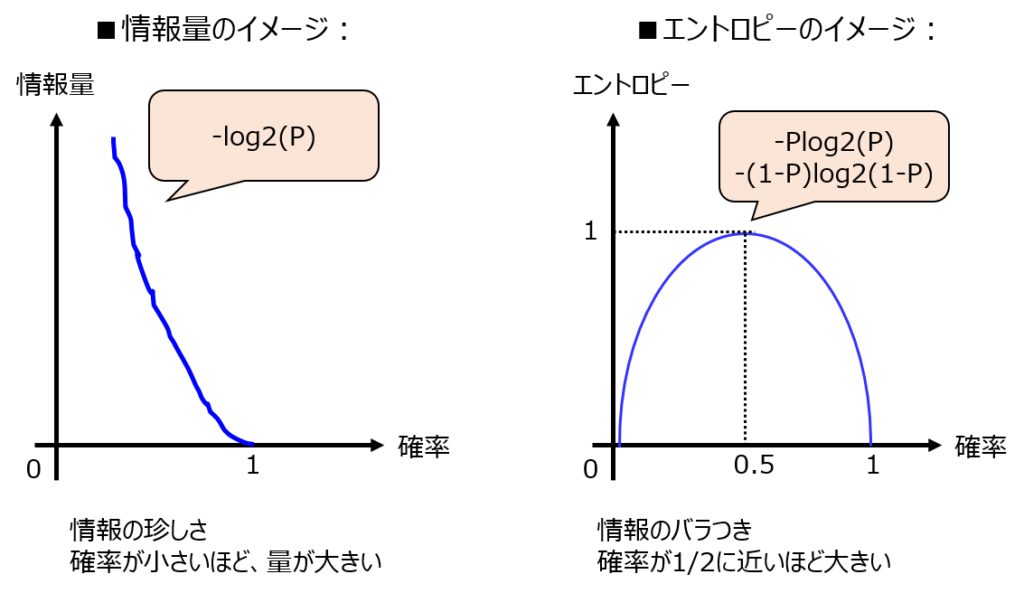
情報の珍しさを示しています。
確率\(P\)の情報源に対する情報量は以下で表されます。
\begin{aligned}i(P)=-\log_{2}P\end{aligned}
確率Pが小さければ小さいほど、その情報は珍しい=情報量が大きいという解釈になります。
院試では、情報量の計算より下記のエントロピーの計算が問われることが多いです。
背景知識として持っておきましょう。
エントロピーとは
情報の乱雑さを表しています。
確率\(P\)の情報源があったとすると、下記の式で表されます。
\begin{aligned}H(P)=-P\log_{2}P\end{aligned}
問題を解くうえでの留意点
最終着地点は(1)式です。各問題で求められている確率\(P\)を求めます。
ただ、問題で提示されている\(P(0)=0.9\)のエントロピーだけを求めても、事象全てのエントロピーを求めたことになりません。
\(P(1)=0.1\)のエントロピーも求め、足し合わせることで初めて事象全体のエントロピーが分かります。
よって、ある事象を二つの構成要素\(P(0),P(1)\)で表されている時、全体のエントロピーは以下になります。(2値エントロピー関数と言います。)
\begin{aligned}H(P)=-P(0)\log_{2}P(0)-P(1)\log_{2}P(1)\end{aligned}
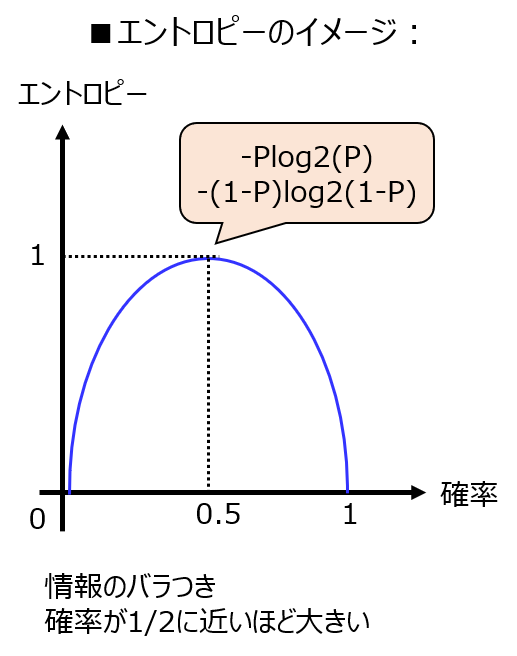
\(P(0)=0.5\)すなわち、確率50%の事象を考える時、事象全体のエントロピーは1となり、最大となります。
一方で、\(P(0)=0,1\)のとき、0で最小となります。
今ある確率が0.5以下のとき、確率が大きくなるとエントロピーは増加傾向。0.5以上の時は減少傾向であるイメージを持っておきましょう。
また、確率0.1のエントロピーと確率0.9の2値エントロピー関数は等しいです。
0.5を境に対称な点は、片方のエントロピーを求めるだけで良いことと覚えましょう。
拡大情報源のエントロピーの計算方法
拡大情報源とは
情報源Sの記号から重複を許してN個を取る順列を作り、それぞれを集合族として表したものです。
例えば、2次の拡大情報源\(S^{2}\)は、\(S^{2}∊{00,01,10,11}\)で表されます。
それぞれの発生確率を求め、エントロピーを足し合わせても良いのですが、下記の式でも求めることができます。
\begin{aligned}H(s^{N})=NH(s^{1})\end{aligned}
1次の情報源のエントロピーに対しN倍することで求めることができます。
知っていれば、すぐに解けますので暗記をオススメします。問題1 (3)でやります。
エントロピーの最大化条件について
ラグランジュの未定乗数法を用います。
以前の記事で類似の説明をしました。
目的の関数を\(H(S)\)、制約条件\(g\)を
\begin{aligned}g(p_{0},p_{1},p_{2},p_{3})=p_{0}+p_{1}+p_{2}+p_{3}-1=0\end{aligned}とし、ラグランジュ関数
\begin{aligned}F(p_{0},p_{1},p_{2},p_{3})=H(S)-\lambda (p_{0}+p_{1}+p_{2}+p_{3}-1)\end{aligned}
とします。
\(\dfrac{\partial F}{\partial p_{0}}=\dfrac{\partial F}{\partial p_{1}}=\dfrac{\partial F}{\partial p_{2}}=\dfrac{\partial F}{\partial p_{3}}=\dfrac{\partial F}{\partial \lambda}=0\)のとき、与えられた制約条件下での\(H(S)\)の極大値になります。
補足
厳密には、ラグランジュの未定乗数法は”極値”を与える際に実施する計算です。関数の素性が不明な場合、極小値を求める可能性もありますが、今回のエントロピー関数は上に凸です。
そのため、求めた極値は極大値にあたります。また、限られた範囲における極大値は、その範囲における最大値を意味しています。
よって、本問の条件下において最大値を求めることができます。
実際に問題を解いて、どのような時に最大値を取るか確認しましょう。
解答例(問題1)
(1)情報量とエントロピー
情報量
\(P(0)=0.9\)のとき、\(H(P(0))=0.15[bit]\)
\(P(1)=0.1\)のとき、\(H(P(1))=3.3[bit]\)
エントロピー
(3)式より
\begin{aligned}H(s)=-(0.9\log_{2}0.9+0.1\log_{2}0.1)=0.465[bit]\end{aligned}
(2)3次の拡大情報源のエントロピー
(4)式の関係より、(5)式の結果を用いれば
\begin{aligned}H(s^{3})=3H(s)=1.395[bit]\end{aligned}
補足
(3)式を用いれば簡単に求められますが、直接計算することでも結果が一致することを確認します。
3次拡大情報源の組み合わせとして、(000,001,010,011,100,101,110,111)の8通りある。
(2)より、1が出る回数が等しければ、0,1が出る順番に依らず発生確率は同じ。発生確率が同じ組み合わせのエントロピーは同じなので、1が出る回数ごとにグループ分けをする。
| 1の出る回数 | 確率 | エントロピー |
| 0回 | \(0.9^{3}=0.729\) | 0.332 |
| 1回 | \(0.9^{2}*0.1=0.081\) | 0.881 |
| 2回 | \(0.9*0.1^{2}=0.009\) | 0.183 |
| 3回 | \(0.1^{3}=0.001\) | 0.010 |
| 合計 | 1.406 |
面倒なので、上記の表はエクセルで計算しました。小数点第2,3位に誤差はありますが、同じであることが確認できました。
解答例(問題2)
まず、\(p_{0}\)について考える。(8)式を\(p_{0}\)で偏微分すると
\begin{aligned}\dfrac{\partial F}{\partial p_{0}}=-\log_{2}p_{0}-\log_{2}e-\lambda=0\end{aligned}
\(p_{1},p_{2},p_{3}\)についても同様の計算が成り立つので
\begin{aligned}p_{0}=p_{1}=p_{2}=p_{3}\end{aligned}
\(\dfrac{\partial F}{\partial \lambda}\)の計算結果は(1)式と一致する。
(1)式と(6)式を連立することにより
\begin{aligned}p_{0}=p_{1}=p_{2}=p_{3}=0.25\end{aligned}
のとき、エントロピー関数\(H(S)\)は最大化する。
解釈
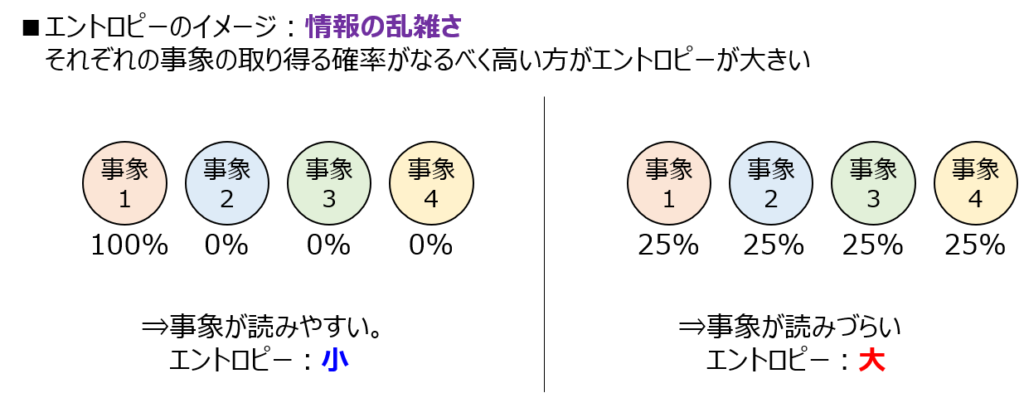
上記のように全ての事象の発生確率が等しいとき、エントロピーが最大化することが分かりました。
もし、情報源の数がn個だとすると、それぞれの事象\(p_{i} \quad i=0,1,\cdots,n\)の確率が全て1/nの時、エントロピー最大になります。
\begin{aligned}H(S)=-\sum ^{n}_{i=1}\log_{2}\frac{1}{n}=\log_{2}n\end{aligned}
上記の原則は、エントロピーの最大原理と呼ばれています。
最後に
エントロピーの最大化条件に関する問題は、意外と院試で出題されます。
本問のように、微分でしっかり計算することも重要ですが、2値エントロピー関数の場合、確率0.5で最大になることも合わせて覚えておくと良いでしょう。