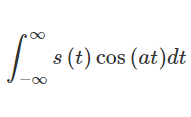ある連続時間信号「s(t)」と三角関数のフーリエ変換

【問】ある連続時間信号\(s(t)\)が存在し、このフーリエ変換を\(S(f)\)と表す。このとき、\(s(t)\cos(2\pi at)\) 及び \(s(t)\sin(2\pi at)\)のフーリエ変換を求めよ。

はじめに
本記事を通して覚えたいこと
周波数シフトについて
解答例
蛇足ですが・・・
最後に
参考文献

はじめに

こちらの問題は、通信工学を少しでも勉強された方であれば、即答できる内容かもしれません。教科書を開けば、当然のように記載してある上式のフーリエ変換ですが、意外にもネットで調べるとあまり紹介されていないように見えます。\(\cos(at)\)、\(\sin(at)\)を単体でフーリエ変換した記事はいくつもありましたが、\(s(t)\)が付いている場合の変換はなかなか見つけられませんでした。

そこで本記事では、今後通信工学の問題を紹介していく上で、非常に重要な考え方が含まれている標記の問題について、解き方を紹介します。

本記事を通して覚えたいこと

オイラーの公式を用いて、三角関数項をexp項に分解する
周波数シフトの考え方を用いると、s(t)の具体的な式を求めないままでもフーリエ変換可能

ポイント1については、\(\cos(at)\)と\(\sin(at)\)のフーリエ変換を計算する際にもよく使います。

まず、\(F\left[ \cos \left( at\right) \right]\)については、

\begin{eqnarray}\int ^{\infty }_{-\infty }\cos \left( at\right) e^{2\pi ft}dt\end{eqnarray}

なので、オイラーの式\begin{eqnarray}\cos \left( at\right) =\dfrac{e^{jat}+e^{jat}}{2}\end{eqnarray}を用いることで、(1)式は

\begin{eqnarray}\dfrac{1}{2}\int ^{\infty }_{-\infty }\left( e^{j2\pi at}+e^{-j2\pi at}\right) e^{-j2\pi ft}dt\end{eqnarray}

と分解できるので、結果は

\begin{eqnarray}F\left[ \cos \left( at\right) \right] = \dfrac{1}{2}\left( \delta \left( f-a\right) +\delta (f+a)\right) \end{eqnarray}になります。

\(F\left[ \sin \left( at\right) \right]\)についても

\begin{eqnarray}\cos \left( at\right) =\dfrac{e^{jat}-e^{jat}}{2j}\end{eqnarray}で与えられるので、同様の計算を行うことで

\begin{eqnarray}F\left[ \sin \left( at\right) \right] =\dfrac{1}{2j}\left( \delta\left( f-a\right) -\delta \left( f+a\right) \right)\end{eqnarray}

を得られます。

周波数シフトについて

\(S(f)\)のフーリエ逆変換を\(s(t)\)とすると、S(f-a)の逆変換は以下の式で表される。

\begin{eqnarray}\int ^{\infty }_{-\infty }S\left( f-a\right) e^{2\pi ft}df\end{eqnarray}

\(f’=f-a\)とおくと

\begin{eqnarray}\int ^{\infty }_{-\infty }S( f’) e^{2\pi ( f’+a) t}df’ =\int ^{\infty }_{-\infty } S\left( f’\right) e^{2\pi f’t}df’ e^{j2\pi at} = s(t) e^{j2\pi at} \end{eqnarray}

と変形することができました。

これは、元の信号\(s(t)\)に\(e^{j2\pi at}\)：周波数a分exp項として掛け算してフーリエ変換すると、変換後の信号スペクトルは、-a分移動することが分かります。

これを周波数シフトと言い、本問はこの事実を活用して解きます。

非常にざっくりとした言い回しで顰蹙を買いそうですが、フーリエ変換対象の信号に対し、exp(at)項を上乗せでかけると、計算後の信号の周波数項は、-a オフセットする。と、ひとまずは覚えても良いかもしれません。

解答例

(i)まず、\(s(t)\cos(at)\)のフーリエ変換\(F\left[ s\left( t\right) \cos \left( at\right) \right]\)を考える。

\begin{eqnarray}\int _{-\infty }^{\infty }s\left( t\right) \cos \left( at\right) dt =\dfrac{1}{2}\int ^{\infty }_{-\infty }(s\left( t\right) e^{-j2\pi \left( f-a\right) t}dt+S\left( t\right) e^{-j2\pi \left( f+a\right) t})dt\end{eqnarray}

周波数シフトの性質により、

\begin{eqnarray}F\left[ S\left( t\right) \cos \left( at\right) \right] =\dfrac{1}{2}( S\left( f-a\right) + S\left( f+a\right))\end{eqnarray}

(ii)次に、\(s(t)\sin(at)\)のフーリエ変換\(F\left[ s\left( t\right) \sin \left( at\right) \right]\)を考える。同様にして

\begin{eqnarray}\int _{-\infty }^{\infty }s\left( t\right) \sin \left( at\right) dt=\dfrac{1}{2j}\int ^{\infty }_{-\infty }(s\left( t\right) e^{-j2\pi \left( f-a\right) t}dt-s\left( t\right) e^{-j2\pi \left( f+a\right) t})dt\end{eqnarray}

同じく、周波数シフトの性質より

\begin{eqnarray}F\left[ S\left( t\right) \sin \left( at\right) \right] =\dfrac{1}{2j}( S\left( f-a\right) – S\left( f+a\right))\end{eqnarray}

が得られる。