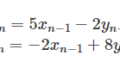あるベクトル空間の集合を組み合わせた基底と写像の次元

問題

(1)\(\mathbb{R} ^{3}\)の2つの部分集合\(W_{1} 、W_{2}\)が下記で与えられているとする。
\begin{eqnarray}W_{1}:=\left\{ \begin{pmatrix} x \\ y \\ z \end{pmatrix}\in \mathbb{R} ^{3}| 2x+5y-z=0\right\} \\ W_{2}:=\left\{ \begin{pmatrix} x \\ y \\ z \end{pmatrix}\in \mathbb{R} ^{3}| 3x+4y+2z=0\right\}\end{eqnarray}
このとき、共通部分\( W_{1} \cap W_{2} \)の基底を求めよ。

(2)下記の行列Aで表される線形写像の核(Kerf)、像(Imf)の基底及び次元を求めよ。
\begin{eqnarray}A=\begin{pmatrix} 5 & -3 & 2 \\ -1 & 1 & 0 \\ -2 & -1 & 1 \end{pmatrix}\end{eqnarray}

はじめに
本記事で覚えたいこと
解答例
最後に
参考文献

はじめに

多くの大学の院試では、固有値を求めて対角化する問題が良く出てきます。こちらは、以前の記事にて説明しました。本日は、基底を求める問題を解説します。このような問題は、電通大などの院試でよく出てきます。

是非、自身が受けようとしている大学の院試問題に基底が出題されているかチェックしてみると良いと思います。

基底と固有ベクトルの違いは下記です。

基底：与えられた行列を構成するそれぞれ一次独立なベクトルの集合
固有ベクトル：基底になるベクトルを線形結合した任意のベクトル

管理人は数学の専門家ではありません。もしかすると、上記の説明では語弊があるかもしれません。

しかし、数学的事実を活用する立場である工学部の院試で得点することを第一に考えるならば、こちらの理解くらいで問題無いと考えています。

本記事で覚えたいこと

与えられたベクトル空間を結合し、行列を作成する
行基本変形し、変数の関係式を求める。関係式を一般化することを基底と呼ぶ。(求めた基底は連立方程式を満たしているので、検算可能)

基底を求めるには、与えられた行列を行基本変形すると良いです。この解法は、巷でも良く解説されています。

本問も、最終的に上記のアプローチに落ち着くことを考えます。しかし、行列がまだ作成できていません。\(W_{1} \cap W_{2}\)の使い方がカギになりそうです。

結論から言うと、\(W_{1}、W_{2}\)を満たすそれぞれの空間を連立し、これを行列にすれば良いです。

慣れていた方ならば、すぐに分かったかもしれません。しかし、院試では間接的な問われ方もするため、本問も同じような表記をしました。ここに気づけば、後は答えを求めることは難しくありません。

(2)写像についての解き方

Ax=0の連立方程式を行基本変形し、行列Aの基底を求める。
基底の数に注目する。核(Kerf)の次元と一致するので、こちらを答えとする。
行基本変形した行列Aの階数に注目。像(Imf)の次元と一致するので、こちらを答えとする。

私が解答作成をしていて困ったことは、ネットで核、像と検索すると定義ばかりヒットすることが多く、問題を解くうえでどう使っていけば良いのか分からないことでした。

厳密な説明は別途必要ですが、問題を解くうえではこちらを意識すると良いと考えています。結論、(1)と同じく行基本変形して出てきたベクトルがKerFの基底。Rankが像(ImF)の基底になっています。カーネル、イメージなど、聞き慣れない言葉が多いですが、要は与えられた行列が座標変換行列ならこのような言われ方をするだけです。

詳しくは、次元定理で検索くださると幸いです。上記の考え方で良い理由が説明されています。

解答例

(1)基底の求め方

\(W_{1}、W_{2}\)を満たすそれぞれの空間を連立すると以下のようになる。

\begin{cases}2x+5y-z=0\\ 3x+4y+2z=0\end{cases}

これを行列表現にし、行基本変形していくと

\begin{aligned}&\begin{pmatrix} 2 & 5 & -1 \\ 3 & 4 & 2 \end{pmatrix}\\ \rightarrow &\begin{pmatrix} 2 & 5 & -1 \\ 0 & -7 & 7 \end{pmatrix} \\ \rightarrow & \begin{pmatrix} 2 & 5 & -1 \\ 0 & -1 & 1 \end{pmatrix} \\ \rightarrow & \begin{pmatrix} 2 & 4 & 0 \\ 0 & -1 & 1 \end{pmatrix} \end{aligned}

より、\(z=y、x=-2y\)が分かる。

よって、求める基底は、\( \left < \begin{pmatrix} -2 \\ 1 \\ 1 \end{pmatrix}\right > \)

検算

\(x=-2,y=1,z=1\)のとき、与えられた連立方程式は以下のようになる。

\begin{cases}-4+5-1=0\\ -6-4+2=0\end{cases}

二つの式両方成立するため、求めた基底が合っていることが確認できた。

(2)写像の基底、次元の求め方

基底について

まず、核(KerF)の基底を考える。(1)と同じく、行基本変形をする。

\begin{eqnarray}A=\begin{pmatrix} 5 & -3 & 2 \\ -1 & 1 & 0 \\ -2 & -1 & 1 \end{pmatrix} \\ → \begin{pmatrix} 0 & 2 & 2 \\ -1 & 1 & 0 \\ 0 & 1 & 1\end{pmatrix} \\ → \begin{pmatrix} 0 & 1 & 1 \\ -1 & 1 & 0 \\ 0 & 0 & 0 \end{pmatrix} \end{eqnarray}

(9)式=0を考えると、以下の関係が分かる。

\begin{eqnarray}\begin{cases}x=y\\ y=-z\end{cases}\end{eqnarray}

以上より、求める基底は\( \left < \begin{pmatrix} -1 \\ -1 \\ 1 \end{pmatrix} \right > \)

次に、像(Imf)の基底を考える。行基本変形の結果(9)式より、1列目と2列目は線形独立であることが分かる。

これは、行列Aの1列目、2列目に対応するので、求める基底は以下の2つ

\( \left < \begin{pmatrix} 5 \\ -3 \\ 2 \end{pmatrix}\right > \left < \begin{pmatrix} -2 \\ -1 \\ 1 \end{pmatrix} \right > \)