【2元対称通信路】無限個接続したときの通信路容量

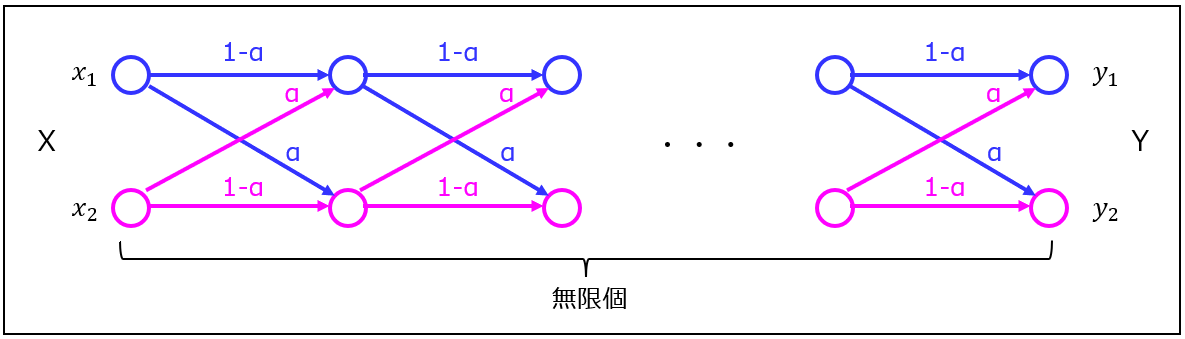
【問】下図のように、誤り確率α<0.5の2元対称通信路が無限個直列に接続されているとする。このときの通信路容量\(C_{\infty }\)を求めよ。

はじめに

2元対称通信路の少し発展的な問題です。

教科書で、1つ接続した場合、2つ接続した場合がよく説明されていますが、無限個接続した場合まではあまり載っていないように感じます。

そこで、本記事では、無限個直列接続した場合の通信路容量の収束値がどのようになるか紹介したいと思います。

この記事を通して覚えたいこと

ポイント1については、情報理論を勉強されている方々ならばご存じの内容と思います。

接続数が何個あっても、その時のX=Y(またはX≠Y)になる確率が分かれば、通信路容量は求まります。

本問でキーとなるのは、ポイント2になります。

数学的な知識ですが、これが抜けているがあまり、計算が進まずに解けない例を見てきました。

試行実験

まず、α=0.1、n=1とし、通信路容量を求めてみます。

通信路行列\(T_{1}\)は、\(\begin{pmatrix} 1-\alpha & \alpha \\ \alpha & 1-\alpha \end{pmatrix}\)で

入力XとYの関係は

\(\begin{pmatrix} x_{1} \\ x_{2} \end{pmatrix}=\begin{pmatrix} 1-\alpha & \alpha \\ \alpha & 1-\alpha \end{pmatrix}\begin{pmatrix} y_{1} \\ y_{2} \end{pmatrix}\)

\(\begin{pmatrix} x_{1} \\ x_{2} \end{pmatrix}=\begin{pmatrix} 0.9 & 0.1 \\ 0.1 & 0.9 \end{pmatrix}\begin{pmatrix} y_{1} \\ y_{2} \end{pmatrix}\)

で表される。

\(x_{1}=y_{1}\)になる確率は、上式より0.9

よって、求める通信路容量\(C_{1}\)は

\(C_{1}=1-H(0.9)\)

\(=1+0.9\log _{2}\frac{9}{10}+0.1\log _{2}\frac{1}{10}\)

\(=0.53\)

通信路が伝送可能な情報量の上限は0.53であることが分かりました。

続いて、n=2のときも考えます。

通信路行列\(T_{2}\)は、\(T_{2}=\begin{pmatrix} 1-\alpha & \alpha \\ \alpha & 1-\alpha \end{pmatrix}^{2}\)

\(T_{2}=\begin{pmatrix} 2\alpha^{2}-2\alpha+1 & 2\left( 1-\alpha\right) \alpha \\ 2\left( 1-\alpha\right) \alpha & 2\alpha^{2}-2\alpha+1 \end{pmatrix}\)

\(T_{2}=\begin{pmatrix} 0.82 & 0.18 \\ 0.18 & 0.82 \end{pmatrix}\) なので

求める通信路容量\(C_{2}\)は、

\(C_{2}=1-H(0.82)=0.32\)

通信路容量が\(C_{1}\)と比較して小さくなることが分かりました。

n=3のときも、さらに小さくなることが予想されます。

しかし、\(T_{3}=\begin{pmatrix} 1-\alpha & \alpha \\ \alpha & 1-\alpha \end{pmatrix}^{3}\)と、手計算することがいよいよ厳しくなってきました。

一般化された\(T_{n}=\begin{pmatrix} 1-\alpha & \alpha \\ \alpha & 1-\alpha \end{pmatrix}^{n}\)を手計算で算出することは困難だと思います。

一般項を推測し、数学的帰納法で証明する方法もあるにはあります。

しかし、今回の行列では管理人は推測することができず、この方法は使えませんでした。

では、どのようにして\(T_{n}\)を求めるのでしょうか。

固有値を用いた対角化

ここで登場するのが、線形代数の知識です。

固有値λを用いて対角行列Pを求めることができれば、後は対角化のルールに従い行列\(T_{1}\)のn乗 \(T_{n}\)を求めることができます。

解答例

固有値をλとし、\(\left| T_{1}-\lambda E\right|\)を考える。

\(\left| T_{1}-\lambda E\right| =\begin{vmatrix} 1-\alpha -\lambda & \alpha \\ \alpha & 1-\alpha -\lambda \end{vmatrix}\)

\(=\left( 1-\alpha -\lambda \right) ^{2}-\alpha ^{2}\\ =\left( 1-\alpha \right) ^{2}-2\lambda \left( 1-\alpha \right) +\lambda ^{2}-\alpha ^{2}\\ =\lambda ^{2}-2p-2\lambda +2\lambda p+1 \\ =\left( \lambda -1\right) ^{2}+2\alpha\left( \lambda -1\right) \\ =\left( \lambda -1\right) \left( \lambda -1+2\alpha\right) \\=0\)

より、固有値\(\lambda=1,1-2\alpha\)が求められる。

(i) \(\lambda=1\)のとき、求める固有ベクトルは

\(\begin{pmatrix} -\alpha & \alpha \\ \alpha & -\alpha \end{pmatrix}\begin{pmatrix} x_{1} \\ x_{2} \end{pmatrix}=\begin{pmatrix} 0 \\ 0 \end{pmatrix}\)

\(x_{1}=x_{2}\)より、\(\begin{pmatrix} 1 \\ 1 \end{pmatrix}\)

(ii) \(\lambda=1-2\alpha\)のとき、求める固有ベクトルは

\(\begin{pmatrix} \alpha & \alpha \\ \alpha & \alpha \end{pmatrix}\begin{pmatrix} x_{1} \\ x_{2} \end{pmatrix}=\begin{pmatrix} 0 \\ 0 \end{pmatrix}\)

\(x_{1}=-x_{2}\)より、\(\begin{pmatrix} -1 \\ 1 \end{pmatrix}\)

よって、対角行列\(P=\begin{pmatrix} -1 & 1 \\ 1 & 1 \end{pmatrix}\)を得る。

これの逆行列は、\(P^{-1}=\begin{pmatrix} -\frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} \end{pmatrix}\)であるので、対角化のルールから

\(T_{n}=\begin{pmatrix} -1 & 1 \\ 1 & 1 \end{pmatrix}\begin{pmatrix} \left( 1-2\alpha \right) ^{n} & 0 \\ 0 & 1 \end{pmatrix}\begin{pmatrix} -\frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} \end{pmatrix}\)

\(T_{n}=\begin{pmatrix} \frac{1}{2}\left( 1-2\alpha \right) ^{n}+\frac{1}{2} & -\frac{1}{2}\left( 1-2\alpha \right) ^{n}+\frac{1}{2} \\ -\frac{1}{2}\left( 1-2\alpha \right) ^{n}+\frac{1}{2} & \frac{1}{2}\left( 1-2\alpha \right) ^{n}+\frac{1}{2} \end{pmatrix}\) を得る。

n→∞の極限を考えると

\(T_{\infty }=\begin{pmatrix} \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} \end{pmatrix}\) になる。

これより、出力Yが入力Xと等しい確率は、1/2となるので

求める通信路容量\(C_{\infty }\)は、

\(C_{\infty }=1-H(0.5)=0\)

何となく予想された方もいらっしゃるのではないでしょうか。

通信路容量0となり、確実に伝送できる情報量が0(無い)になりました。

誤り率が0より大きい2元対称通信路を無限個接続すると、正常な出力値と誤った出力値が出力される確率がイーブンになり、誤り率0.5の通信路を1本接続した場合と等価になりました。

最後に

専門科目ばかり勉強していると、一般教養(数学)の知識が疎かになってしまうことがあります。

そういった時に今回のような問題に当たってしまうと、数学的な知識が抜けているために得点できないという悲しい結果になってしまいます。

重箱の隅をつつく範囲までは厳しいですが、計算方法の引き出しを持っておくための数学の勉強は、定期的に行った方が良いかもしれません。

参考文献

大学院入試問題 : 解法と演習：関, 正治. 陳, 啓浩. 姫野, 俊一(著) 第2章