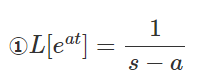はじめに
本記事は、問題形式での紹介ではありません。
筆者が電気情報系の院試問題を解いてきて、覚えていると楽に感じたラプラス変換(逆変換)の公式について紹介していきます。
「ラプラス変換 公式」でググると、詳細一覧が出てきますが、その中で選り好みしたものを紹介します。
前提
電気情報系の院試でラプラス変換を特に使用する分野は、「数学」「電気回路(過渡現象)」「制御工学」の3つです。
本記事では、総合的に判断した結果を示します。しかし、分野ごとによく使用する公式とそうでないものが分かれるのも事実です。
公式ごとに使用する分野も明記しています。それらも踏まえて、暗記の重要度などを最終判断くださればと思います。
また、ここで紹介しなかった公式が本番で必要で失点した責任は取れないですので、ご了承ください。
暗記必須 (6個)
①\(L[e^{at}]=\dfrac{1}{s-a}\)
これはコメント不要でしょう。ラプラス変換を試験範囲とする大学の院試で必ず使います。覚えやすくもありますので、まだの方はこの機会に是非覚えましょう。
単位ステップ関数のラプラス変換、\(L[1]=\frac{1}{s}\) もこちらの公式に含まれています。
②\(L[t]=\dfrac{1}{s^{2}}\)
制御工学の分野で特に使う公式です。(定常速度偏差の算出で)
数学としてのラプラス変換を出題する場合だと出現度は落ちますが、変わらず重要なのでこちらで紹介します。
③\(L[\cos \omega t]=\dfrac{s}{s^{2}+\omega^{2}}\)
数学、制御工学ともによく使う公式です。本サイトでは、問題文に補足として提示しています。しかし、院試では提示してくれない大学が多いです。
このため、覚えておくことを推奨します。
④\(L[\sin \omega t]=\dfrac{\omega}{s^{2}+\omega^{2}}\)
3.と同じ理由です。分子だけ違います。
どっちがどっちなのか、ド忘れしてしまうことがあります。
筆者としては、両辺の分子にsが付くのは1か所だけという覚え方をしています。(sinだと、左辺の”s”inの部分で1つsが付くので、右辺の変換結果にはsが付かない。cosは逆。)
⑤\(L[f'(t)]=sF(s)-f(0)\)
電気回路の過渡現象でよく使う公式です。コイルLが素子にあると使います。数学としても、本公式の導出問題は良く出てきます。
他、制御工学でも偏差の補償問題に出てくることがあります。よって必須級です。
筆者はよく、\(L\dfrac{di}{dt}=LsF(s)-f(0)\)と、\(f(0)\)項にLをかけ忘れる計算ミスをしてしまいます。(本当は、\(Lf(0)\))試験本番ではこのようなことが無いよう、注意すると良いと思います。
⑥\(L\left[ \int _{0}^{t}x\left( t’\right) dt’\right] =\dfrac{X\left( s\right) }{s}\)
こちらも電気回路の過渡現象でよく使う公式です。コンデンサ成分Cがあると使います。
しかし、数学ではあまり使わないため、こちらのみの選択の受験者は必須では無いかもしれません。
制御としては偏差の補償問題で使用することがあるので、多数決で必須と分類しました。
覚えておくと便利な公式 (4個)
⑦\(L[u(t-a)]=e^{at}\)
時間推移則です。電気回路の過渡現象の問題で、単位ステップ入力を途中で0にする矩形波入力を実現するときに使います。数学でも、このタイプの関数はたまに出題されますので、覚えておくと良いかもしれません。
(最悪、ラプラス変換の公式に当てはめると導出できますが・・・)
⑧\(L\left[\dfrac{1}{s\left( s+a\right) }\right]=\dfrac{1}{a}\left( 1-e^{-at}\right) \)
あまり紹介されない式ですが、電気回路を選択される方は覚えておいた方が良いと思います。
0ではないある一定値に収束することから、LR回路に流れる電流の時間応答を求めるときなど、こちらの公式を使用します。
公式を覚えてなくとも、部分分数分解すると解くことはできます。しかし、時間短縮と使用頻度の観点から覚えておくことを推奨します。
⑨\(L[\left( e^{at}\cos \omega t\right)] =\dfrac{s-a}{\left( s-a\right) ^{2}+\omega ^{2}}\)
この複雑さになってくると、問題文で提示して欲しいのが管理人の本音です。しかし、残念なことに3.4.と同じく紹介しない大学が多いです。阪大、神戸大でこちらの変形を使用したことがあるため、左記の大学を志望される方は覚えておいた方が良いかもしれません。
⑩\(L[\left( e^{at}\sin \omega t\right)] =\dfrac{\omega}{\left( s-a\right) ^{2}+\omega ^{2}}\)
上記と同様です。結局、分子にsが付くcosに-aの項が付くと考えると暗記の助けになるかもしれません。
補足
単位インパルス関数のラプラス変換
\begin{eqnarray}L\left[ \delta \left( t\right) \right] =1 \end{eqnarray} についてはあえて記載しませんでした。
インパルス関数の定義により、\(\delta (0)=1\)のとき、一緒に乗算している値を掛け合わせると、結果が導出できるからです。
\begin{eqnarray}\int ^{\infty }_{-\infty }f\left( t\right) e^{-st}dt\end{eqnarray}
の場合、\(t=0\)のとき、\(e^{-st}=1\)だから、(1)式は成立する。
最後に
本記事のような説明はいかがでしょうか。初の試みでしたが、好評の際は他の分野でも行おうかと思います。