【分布定数回路】反射係数とインピーダンス整合、定在波比の関係

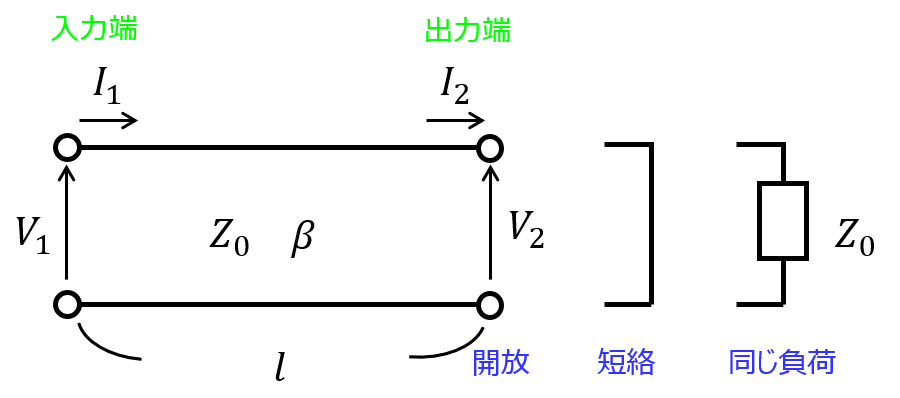
以下の無損失分布定数回路を考える。特性インピーダンスを$Z_0$とする。(i)出力端を開放したとき、(ii)短絡したとき、(iii)特性インピーダンスと同じ負荷を接続したとき、3パターンにおける電圧反射係数を求めよ。

はじめに

このタイプの問題も、分布定数回路の問題の典型パターンの一つです。分布定数回路の概要については、以前の記事で説明しています。よろしければご確認くださると幸いです。

この記事で覚えてほしいこと

反射係数の意味

入力電圧$V_x^{+}$に対しての反射電圧$V_x^{-}$の比を表します。

$$\begin{array}{}\text{(1)}& \mathrm{\Gamma }={\displaystyle \frac{V_x^{-}}{V_x^{+}}}={\displaystyle \frac{V_x-Z_0{I}_x}{V_x+Z_0{I}_x}}={\displaystyle \frac{Z_x-Z_0}{Z_x+Z_0}}\end{array}$$

ただし、$x$は入力端からの距離を示します。出力端の場合は、〆CHECK1で示した式になります。

式(1)の分子に注目すると、入力端から位置xの距離にあるインピーダンス$Z_x$が特性インピーダンスと等しいとき、その地点での反射係数0になります。(反射波が発生しない)

これをインピーダンス整合と言います。実際の工学機器を作成していく上で、非常に重要な現象になっています。

インピーダンス整合が役立つ場面

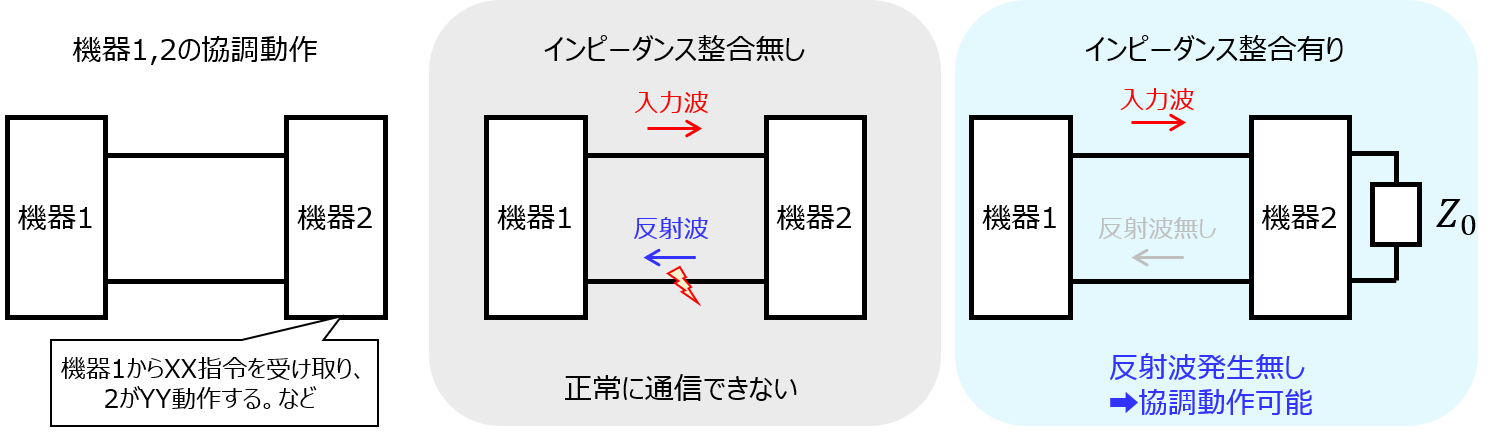
例えば、下記の図のように、機器1,2で通信することを考えます。

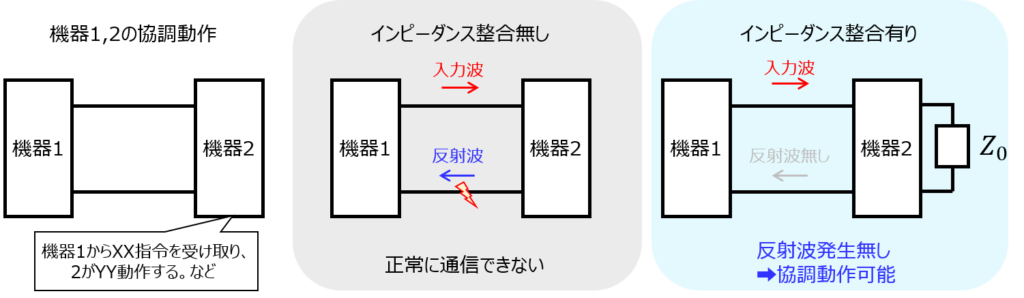
機器1から情報を送信する際、反射波が発生するとノイズになってしまいます。こうなると機器2は正しく情報受信できず、両者の協調動作ができなくなってしまいます。

これを解決するため、機器2に特性インピーダンスと同じ大きさの終端抵抗を設け、反射波を無くす手法が様々な現場で用いられています。

院試対策も重要･･･なのですが、将来メーカーへ就職した際に出てくるかもしれない技術です。

「インピーダンス整合」と言うキーワードだけは忘れないようにしましょう。

解答例

出力端を開放した場合

出力端に接続するインピーダンス$Z_2$は、∞になる。

このときの反射係数は、$\mathrm{\Gamma }={\displaystyle \frac{1-{\displaystyle \frac{Z_0}{Z_2}}}{1+{\displaystyle \frac{Z_0}{Z_2}}}}=1$

入力波と同じ大きさの反射波が発生します。

出力端を短絡した場合

前節とは逆に、出力端に接続するインピーダンス$Z_2$は、0になる。

このときの反射係数は、$\mathrm{\Gamma }={\displaystyle \frac{0-Z_0}{0+Z_0}}=-1$

絶対値を取ると1です。入力波と同じ大きさの反射波が同じく発生します。

特性インピーダンスと同じ負荷を出力端に接続した場合

前章で答えを出してしまったのですが、このときの反射係数は下記の式になります。

$\mathrm{\Gamma }={\displaystyle \frac{Z_0-Z_0}{Z_0+Z_0}}=0$

物理的なイメージですが、下記のようになります。

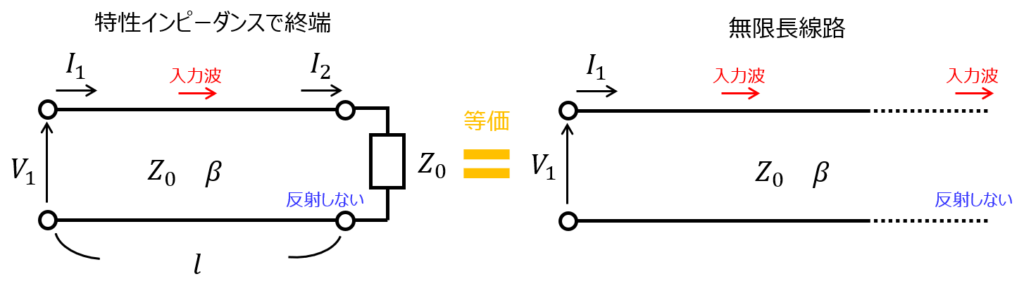
特性インピーダンスと同じ負荷が接続されているので、無限長線路で考えることができます。このため、反射波は発生しません。

発展：定在波比について

本問の発展版として、「出力端における電圧定在波比(VSWR)を求めよ。」という問題が出てくる場合もあります。発展版として、定在波の物理現象の説明と解法について紹介します。

定在波比とは

入力波$V_x^{+}$と反射波$V_x^{-}$を合計した波の振幅：最大値と最小値の比を表します。

下記のように式変形できることから、反射係数が分かれば、定在波比$\rho$が分かります。

$$\begin{array}{}\text{(2)}& \rho ={\displaystyle \frac{V_x^{+}+V_x^{-}}{V_x^{+}-V_x^{-}}}={\displaystyle \frac{1+{\displaystyle \frac{V_x^{-}}{V_x^{+}}}}{1-{\displaystyle \frac{V_x}{V_x^{+}}}}}={\displaystyle \frac{1+\left|\mathrm{\Gamma }\right|}{1-\left|\mathrm{\Gamma }\right|}}\end{array}$$

仮に、特性インピーダンス$50[\Omega ]$、出力端に接続する抵抗が$25[\Omega ]$だとします。このとき、下記の式から定在波比は${\displaystyle \frac{1}{3}}$になります。

$$\begin{array}{}\text{(3)}& \left|\mathrm{\Gamma }\right|=\left|{\displaystyle \frac{25-50}{25+50}}\right|={\displaystyle \frac{1}{3}}\end{array}$$

$$\begin{array}{}\text{(4)}& \rho ={\displaystyle \frac{1+\left|\tau \right|}{1-\left|\tau \right|}}={\displaystyle \frac{4}{3}}\cdot {\displaystyle \frac{3}{2}}=2\end{array}$$

仮に、出力端に接続する抵抗が特性インピーダンスと同じ$50[\Omega ]$のときは、反射波が発生していない状態になります。このとき、合成波は入力波と同じ値を取るため、定在波比は1になります。

理論上、反射波が発生しないほうが、入力信号を出力端で受信できる割合が大きくなり、効率が良くなります。実際の回路設計では、定在波比1を目標にすることが多いです。

最後に

類題として、出力端に$Z_2=R+jX$なる抵抗性負荷とリアクタンスを接続する問題が出題されることがあります。

この時、反射波が発生しない条件を求めよ。インピーダンス整合する条件を求めよ。など、色々な問われ方をします。しかし、結局は式(1)の関係から、反射係数0にするように条件式を立てることに帰着するケースが多いです。

また、本問は、出力端での値を問いましたが、出力端/出力端から長さ$l$進んだ地点など、場所が変わることがあります。

結局、その場所から見た駆動点インピーダンスを求め、反射係数を求めると、同じ方針で求めることができますが、機会があれば紹介したいと思います。

参考文献

電磁波工学：安達三郎(著) 電子情報通信学会シリーズ 第5章