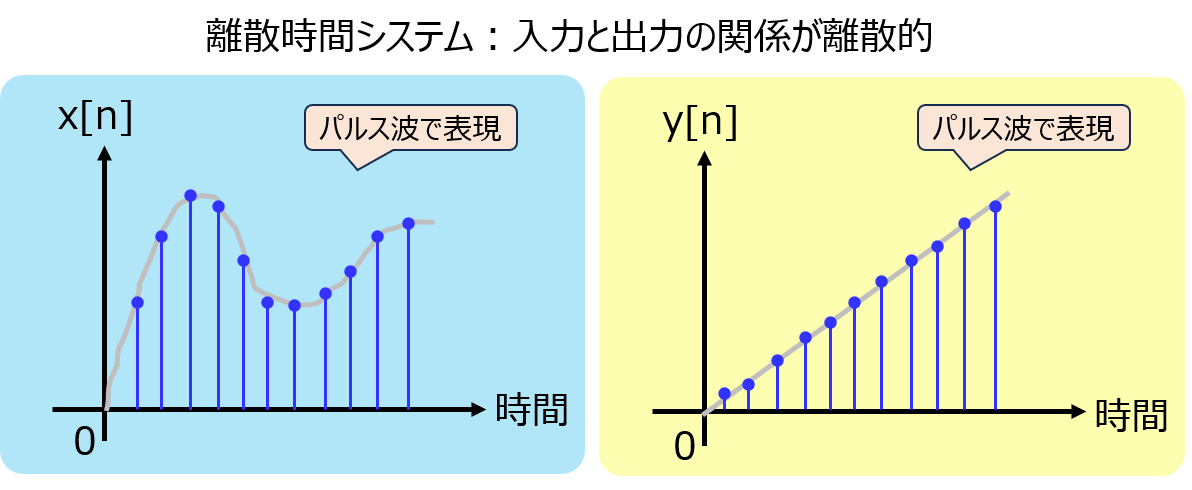
下記の信号(a)~(f)それぞれにおいて、記憶性、線形性、時不変性、因果性を満たすものを述べよ。
\((a)y[n]=x[3n]\)
大阪大学 電気電子通信情報専攻 2023 院試問題 信号処理1. から引用 (一部数値を改変)
\((b)y[n]=\Sigma^{\infty}_{k=-\infty}x[k]\)
\((c)y[n]=\Sigma^{n}_{k=-\infty}2^{k-n}x[k]\)
\((d)y[n]=n^{2}x[n]\)
\((e)y[n]=(x[n])^{2}\)
\((f)y[n]=x[n]+1\)
\((g)y[n]=x[-n]\)
離散時間システムとは
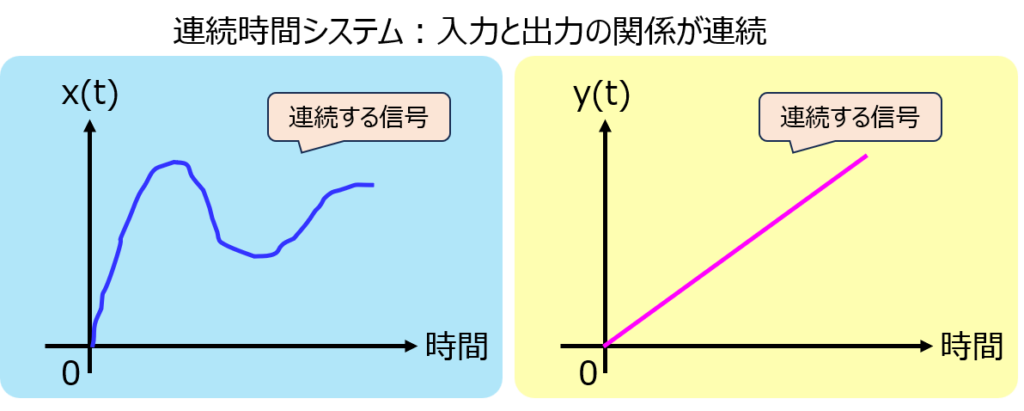
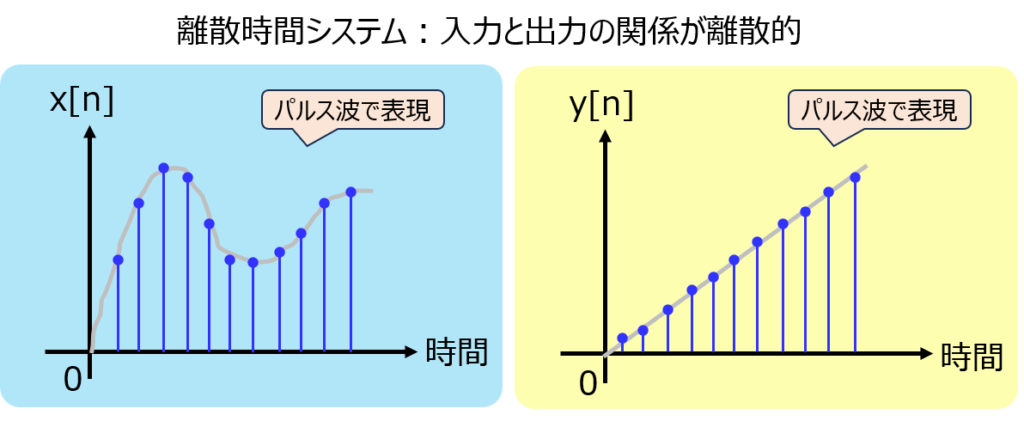
あるシステムにおいて、入力信号と出力信号の関係が離散時間信号で表されるものを言います。システムをLと置くと
\begin{aligned}y[n]=L[x[n]]\end{aligned}
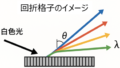
で表されます。離散時間のため、時間は整数nで表します。連続時間システムの場合、時間はtなので
\begin{aligned}y[t]=L[x[t]]\end{aligned}
になります。通信方式、制御工学では連続時間で議論することが多いですが、本記事ではディジタル信号処理で扱う離散時間システムの性質に対して議論していきます。
離散時間システムの性質
記憶性
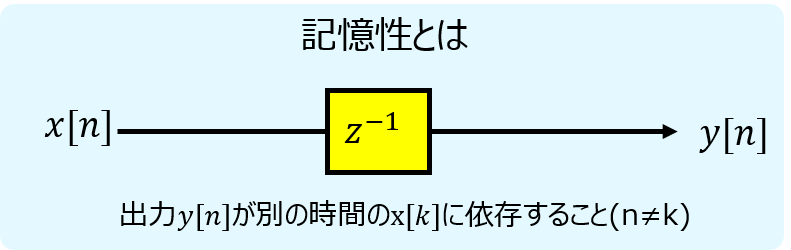
ある時間t,nにおけるシステムの出力が、同時刻以外の入力に依存することを言います。
例えば、\(y[n]=x[n-1]\)なる差分方程式を実現するシステムを考えたとき、ある周期nの出力yは、一つ前の周期の入力xに依存することが分かります。同時刻以外の入力により、出力が決まっているので、記憶性がある。と言えます。
基本的に、与えられた差分方程式の形を見て、n-k (k:0以外の整数)など、nとは別の時間があれば、記憶性があると見て良いです。下記で見ていきましょう。
\((a)y[n]=x[3n]\)について:
出力nは、別の時間3nの入力に依存するため、記憶性がある。
\((b)y[n]=\Sigma^{\infty}_{k=-\infty}x[k]\)について:
別の時間の入力x[n-k]の重ね合わせのため、記憶性がある。(c)も同じ。
\((d)y[n]=n^{2}x[n]\)について:
y[n]は、同じ時間の入力x[n]のみに依存するため、記憶性は無い。(e),(f)も同じ。
\((g)y[n]=x[-n]\)について:
別の時間の入力-nに依存するため、記憶性がある。
線形性
あるシステムの出力y[n]の線形結合は、入力x[n]の線形結合で表されることを言います。
具体的には、あるシステムLの入力出力関係は、下記の式で表されます。
\begin{aligned}L[ax_{1}+bx_{2}]=aL[x_{1}]+bL[x_{2}]\end{aligned}
問題を解くうえでは、与えられた式が上記のような式変形ができるのかを見ていけば良いです。
\((a)y[n]=x[3n]\)について:線形性がある。
\begin{aligned}y[n]&=L[x[3n]] \\ &=ax_{1}[3n]+bx_{2}[3n] \\ &=ay_{1}[n]+by_{2}[n]\end{aligned}
\((b)y[n]=\Sigma^{\infty}_{k=-\infty}x[k]\)について:線形性がある。
\begin{aligned}&\Sigma^{\infty}_{k=-\infty}(ax_{1}[n]+bx_{2}x[n]) \\ &=a\Sigma^{\infty}_{k=-\infty}x_{1}[k]+a\Sigma^{\infty}_{k=-\infty}x_{2}[k] \\ &= ay_{1}[n]+by_{2}[n]\end{aligned}
\((c)y[n]=\Sigma^{n}_{k=-\infty}2^{k-n}x[k]\)も、(b)と同様の変形ができるので、線形性がある。
\((d)y[n]=n^{2}x[n]\)について:\(n^{2}\)の係数が\(x[n]\)にかかっているものの、\(x[n]\)自体は、(a)と同じ変形ができるため、線形性がある。
\((e)y[n]=(x[n])^{2}\)について:線形性は無い。
下記の式変形により、\(x_{1}x_{2}\)の積項が現れるため。
\((ax_{1}+bx_{2})^{2}=a^{2}x_{1}^{2}[n]+abx_{1}[n]x_{2}[n]+b^{2}x_{2}^{2}[n]\)
\((f)y[n]=x[n]+1\)について:線形性は無い。
下記の式変形は成立せず、(3)式の形に変形できないため。
\(L[ax_{1}[n]+bx_{2}[n]+1]≠L[a(x_{1}[n]+1)+b(x_{2}[n]+1)]\)
\((g)y[n]=x[-n]\)について:線形性がある。
符号が逆になっているものの、(a)の変形は同様に成立する。
結局、入力が2乗になっていたり、定数入力が与えられているときは線形性が無いことが分かりました。
時不変性
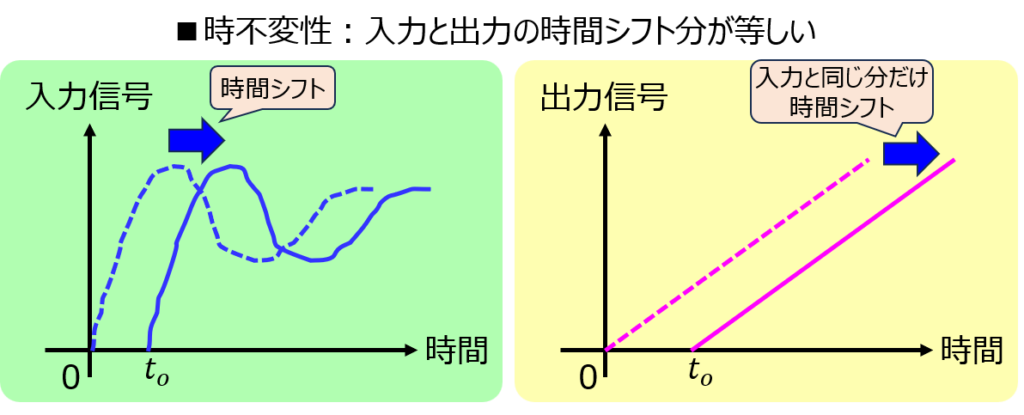
入力x[n]をある時間\(n_{o}\)だけ時間シフトすると、出力も\(n_{o}\)分シフトすることを言います。
\begin{aligned}y[n-n_{o}]=L[x[n-n_{o}]]\end{aligned}
\((a)y[n]=x[3n]\)について:時不変性は無い。
\(x[3n-n_{o}]≠x[3(n-n_{o})]\)が成立しないから。
\((b)y[n]=\Sigma^{\infty}_{k=-\infty}x[k]\)について:時不変性がある。
与えられた式は無限級数のため、時刻をシフトしたからと言って、全体の入力は変化しない。
\((c)y[n]=\Sigma^{n}_{k=-\infty}2^{k-n}x[k]\)について、時不変性は無い。
こちらは有限の級数のため、時間シフトの影響を受ける。\(x_{1}[n]=x[n-n_{o}]\)を入力したときの出力を\(y_{1}[n]\)とすると
\begin{aligned}y_{1}[n]=L[x_[n]]=\Sigma^{n}_{k=-\infty}2^{k-n}x[n-n_{o}]\end{aligned}
\begin{aligned}y[n-n_{o}]=\Sigma^{n-n_{o}}_{k=-\infty}2^{k-n+n_{o}}x[n-n_{o}]≠y_{1}[n]\end{aligned}
が非成立のため。
\((d)y[n]=n^{2}x[n]\)について:(c)と同じ議論により、時不変性は無い。
\((e)y[n]=(x[n])^{2}\)について:xと同じ離散時間nの入力に対しy[n]が決まる。時間シフトした時もこの性質は変わらないため、時不変性がある。(f)も同じ
\((g)y[n]=x[-n]\)について:時不変性は無い。
\(y[n-n_{o}]=x[-(n-n_{o})]≠y_{1}[n]\)だから。
因果性
ある時刻nのときの出力y[n]が、過去の入力x[-∞]~x[n]で決まること。を言います。
よって、冒頭で与えられた式(a)~(g)のうち、n+1以降の時間を入力として持っているものは因果性を満たさないことになります。((a),(b),(g)について、因果性はありません。(g)は、nが負のときに因果性を満たさなくなります。)
一方で、(c),(d),(e),(f)はnまでの時間で出力が決まるので、因果性はあります。
最後に
~~性はある。無い。という言葉で記事を書きましたが、筆者の中ではもう少し綺麗な日本語になるのではないかと思っています。適切な言葉があれば、こっそり教えてください。