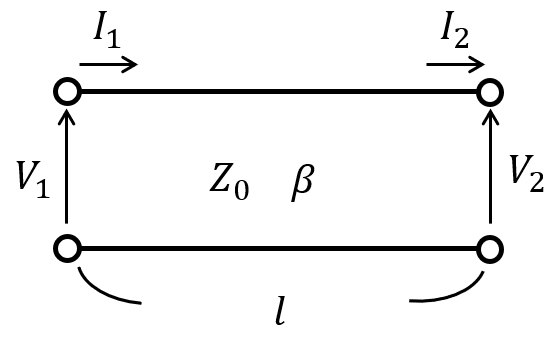
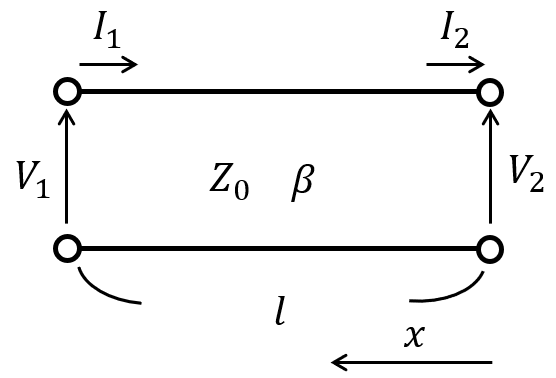
以下の無損失分布定数回路を考える。(i)出力端を開放したとき、(ii)短絡したときの入力端から見た入力インピーダンス\(Z_{1}\)、\(Z_{2}\)を求めよ。
また、出力端から\(x<l\)の位置での駆動点インピーダンスを(i),(ii)の場合それぞれ求めよ。
なお、特性インピーダンスを\(Z_{0}\)とし、入力端と出力端の長さを\(l\)、位相定数を\(\beta\)とする。
はじめに
分布定数回路は特定の大学の院試に出てきます。マイナーな範囲であるが故、演習が積みづらい分野となります。
電信方程式からの基本方程式の導出はネットでよく見かけますが、実際に求値問題となったときの解き方を解説しているサイトは少ないと感じました。
そこで、本記事では分布定数回路の問題に対する一般的な解法の方針を紹介し、実際に出力端を開放、短絡したときの入力インピーダンスを求めてみます。
集中定数回路と分布定数回路の違い
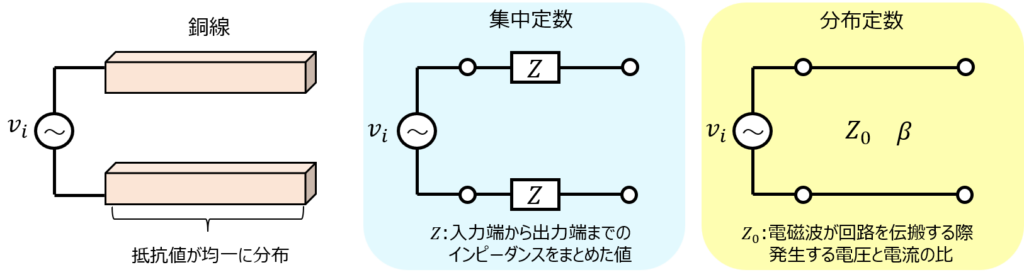
一般的な電気回路に関する問題は、集中定数回路としています。銅線を例に取ると、どこか一か所に抵抗値が集中しているわけではなく、現実的には均等に抵抗値が分布しているはずです。
ですので、電気回路解析をする際、本来は銅線を微小区間分割し、区間ごとに電流の変化を求めていかなければなりません。しかし、集中定数回路はこの影響を無視しています。
集中定数とすることで、節点間の電流は一定値としてみなすことができ、解析が容易になります。
一方で、分布定数回路は、集中定数と逆で、区間ごとの電流の変化を無視しません。
特に、物理的に距離が長い回路に使用され、送電線が良い例です。
こういったとき、分布定数回路を用いて、問題で与えられた回路の特性を考えていくことになります。
解法の方針
- 基本方程式を立てて、2端子対回路問題に帰着する。
- 伝搬定数\( \gamma \)を確認し、双曲線関数項を変形する。
- 2次側の項に問題の条件を代入する。
- 入力端の電流、電圧の比を取り、入力インピーダンスを求める。
- ある点\(x\)における駆動点インピーダンスは、出力端に対する長さを基本方程式に対して置き換え、1~4と同様の手順で求められる。
特に重要な手順が、最初の「基本方程式を立てる」作業になります。
ここが書ける = 分布定数回路の問題で得点できる。と言っても過言ではありません。
解答例
基本方程式を立てる
入力端に流れる電流、電圧を\(I_{1} , V_{1}\)、出力端に流れる電流を\(I_{2} , V_{2}\)とすると
\begin{cases}V_{1}=V_{2}\cosh \gamma l+Z_{0}I_{2}\sinh \gamma l\\ I_{1}=\frac{V_{2}}{Z_{0}}\sinh \gamma l +I_{2}\cosh \gamma l\end{cases}
分布定数回路の問題は、入力インピーダンスを求めるか、インピーダンス整合を考えることが多く、いずれにも使われます。
まずは、騙されたと思って上式を暗記してください。
分布定数回路の問題がとっつきにくいと言われる理由の8割が、解き方が集中定数回路と異なることだと考えています。
しかし、上式さえ書けてしまえば、後は集中定数における2端子対回路の問題と同様の解き方になります。(少なくとも大学レベルでは)
導出については、他サイトでも頻繁に取り上げられています。機会があれば、本サイトでも取り上げたいですが、しばらくはネット検索をお願いします。
伝搬定数\(\gamma\)を確認し、双曲線関数項を変形する
伝搬定数\(\gamma\)は、以下の式で表すことができます。
\begin{eqnarray}\gamma = \alpha +j \beta\end{eqnarray}
ただし、\(\alpha\)は減衰定数、\(\beta\)は位相定数を表す。
無損失線路のとき、\(\alpha=0\)だから、\begin{eqnarray}\gamma = j \beta\end{eqnarray}
\(\sinh j\beta l=j\sin\beta l , \cosh j\beta l=\cos\beta l\)より、基本方程式は
\begin{cases}V_{1}=V_{2}\cos \beta l+jZ_{0}I_{2}\sin \beta l\\ I_{1}=j\frac{V_{2}}{Z_{0}}\sin \beta l +I_{2}\cos \beta l\end{cases}
と書き直せる。
ここまで来れば、答えはもうすぐです。
2次側の項に問題の条件を代入し、入力インピーダンスを求める
解法の方針3.4.で紹介した手順を一度にやります。
(i) 2次側を開放したとき、\(I_{2}=0\)だから
\begin{cases}V_{1}=V_{2}\cos \beta l\\ I_{1}=j\frac{V_{2}}{Z_{0}}\sin \beta l \end{cases}
入力インピーダンスは、\begin{eqnarray}Z_{1}=\dfrac{V_{1}}{I_{1}}=\dfrac{Z_{0}\cos \beta l}{\sin \beta l}=-\dfrac{j Z_{0}}{\tan \beta l}\end{eqnarray}
(ii) 2次側を短絡したとき、\(V_{2}=0\)だから\begin{cases}V_{1}=jZ_{0}I_{2}\sin \beta l\\ I_{1}=I_{2}\cos \beta l\end{cases}
入力インピーダンスは、\begin{eqnarray}Z_{2}=\dfrac{V_{1}}{I_{1}}=Z_{0}\tan\beta l\end{eqnarray}
を得る。
位置\(x\)における駆動点インピーダンス
前節までは、入力端から見た入力インピーダンスを考えました。
今度は、線路上のある位置\(x\)から出力端を見た駆動点インピーダンス\(Z_{x}\)を考えます。
一見、難しそうに見えますが、入力インピーダンスを求める計算と変わりません。
位置が\(l→x\)になるため、基本方程式は下記のようになる。
\begin{cases}V_{1}=V_{2}\cos \beta x+jZ_{0}I_{2}\sin \beta x\\ I_{1}=j\frac{V_{2}}{Z_{0}}\sin \beta x +I_{2}\cos \beta x\end{cases}
これを見て、気づいたことは無いでしょうか。そうです。(4)式に対し、長さが\(l→x\)に変わっただけです。
このように、線路の途中のインピーダンスを求める場合においても、比較対象の地点の長さが分かれば、基本方程式で結果が求められます。
あとは、前節と同じ計算を行えば良いので
(i)出力端を開放したとき:
\begin{eqnarray}Z_{1}=\dfrac{V_{1}}{I_{1}}=\dfrac{Z_{0}\cos \beta x}{\sin \beta x}=-\dfrac{j Z_{0}}{\tan \beta x}\end{eqnarray}
(ii)出力端を短絡したとき:
\begin{eqnarray}Z_{2}=\dfrac{V_{1}}{I_{1}}=Z_{0}\tan\beta x\end{eqnarray}
と、答えも長さ項を置き換えただけになりました。
最後に
分布定数回路は、本問の解き方がベースとなります。
次回以降は、もう少し複雑な回路条件下での計算、インピーダンス整合や、定在波など、順に扱いたいと思います。
なお、電気主任技術者試験では、分布定数回路の過渡現象も出題されています。こちらは、本記事に当てはまらない特別な解き方をします。他解説サイト様を検索下さればと思います。
分布定数回路に関する他記事
(2024/1/17 追記)「分布定数回路」に関する検索ワードで本サイトを訪問下さる方が多いです。
本記事は、基本的な解法紹介でしたが、下記の記事で進んだ内容を紹介しています。是非ご覧ください。
反射係数に関する記事
並列接続に関する記事
異なる特性インピーダンスを直列接続した場合
スミスチャートを利用した解法
分布定数回路の過渡現象
参考文献
電気回路 -三相,過渡現象,線路-:喜安 善一(著)、斎藤 伸自(著) 第8章