論理関数\(f_{1}\left( x_{1},x_{2},\ldots ,x_{i},\ldots ,x_{j},\ldots x_{n}\right)\)の\(x_{i},x_{j}\)を入れ替えた
関数\(f_{2}\left( x_{1},x_{2},\ldots ,x_{j},\ldots ,x_{i},\ldots x_{n}\right)\)の\(x_{i},x_{j}\)を考える。
任意の\(i,j\)について\(f_{1},f_{2}\)の出力が等しいとき、n変数対称関数と言う。
n個の変数のうち、過半数以上の変数が1であるときのみ1を出力する関数をn変数多数決関数と言う。
(1)n変数対称関数は何個存在するか。
(2)多数決関数は、対称関数かつ自己双対関数であることを示せ。
(3)ある論理関数\(f\)が対称ならば、\(f\)の双対関数は対称であることを示せ。
はじめに
論理関数に関する問題の続きです。以前の記事では、自己双対関数、線形関数をそれぞれ紹介しました。まだの方は是非ご覧ください。
本記事で覚えたいこと
- 対称関数は、変数のうち1である数字の数の組み合わせで総数が決まる
- 多数決関数の否定を取ると、過半数を超えない変数が1のとき、出力も1になる
1.について、例えば2変数対称関数\(f\)を考えます。
どのような変数の入力の組み合わせでも1を出力する場合を考えると
1を取る変数が0つのとき、\(f_{0}=\overline{x}\overline{y}\)
1を取る変数が1つのとき、\(f_{1}=x\overline{y}+\overline{x}y\)
1を取る変数が2つのとき、\(f_{2}=xy\)
これを全て組み合わせて、\begin{eqnarray}f=f_{0}+f_{1}+f_{2}=\overline{x}\overline{y}+x\overline{y}+\overline{x}y+xy\end{eqnarray}
もし、1を取る変数が1つのときは0を出力するならば、\(f_{1}=0\)とし、\begin{eqnarray}f=\overline{x}\overline{y}+xy\end{eqnarray}とできます。
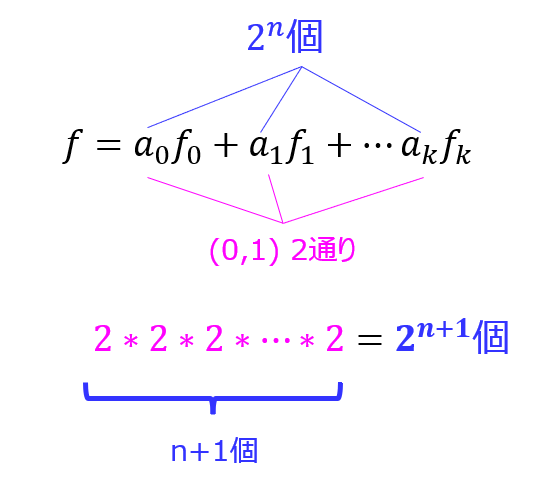
このように、n変数対称関数は、\begin{eqnarray}f=a_{0}f_{0}+a_{1}f_{1}+ \ldots + a_{n}f_{n}\end{eqnarray}のうち、\((a_{0},a_{1},\ldots ,a_{k}) \in(0,1)\)が取る組み合わせで個数が決まります。
2.については、記載した通りです。イメージ通りだと思いますが、(2)(3)でこの考え方を利用します。
解答例
(1)n変数対称関数の個数
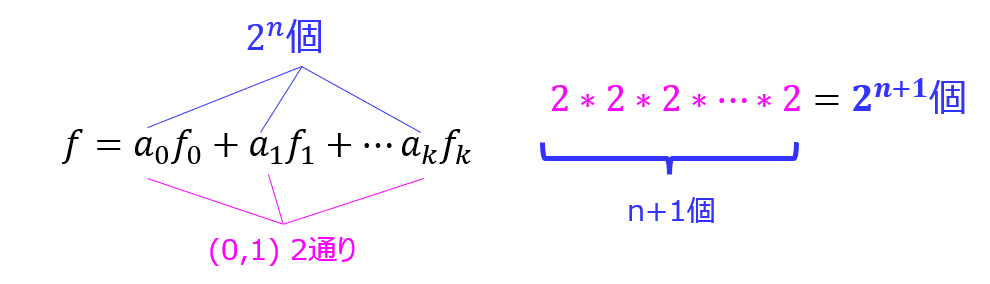
式(3)より、\(a_{i}\)\(i=0,1, \ldots ,n\)は0か1を取り、\(i\)は合計n+1個存在するので
\(2*2*2* \ldots *2=2^{n+1}\)個存在する。
過去記事で紹介した、n変数線形関数と同様の考え方に帰着できました。
(2)多数決関数の対称性、自己双対性
対称性について
多数決関数は、\(n=2m+1\)\(m=0,1,2, \ldots\)としたとき
式(3)の\(\left[ \frac{2m+1}{2}\right]<k\)を満たす\(a_{k}\)に対し、全て\(a_{k}=1\)を代入。
\(\left[ \frac{2m+1}{2}\right]<k\)未満は、全て\(a_{k}=0\)を代入することで実現できます。
\begin{eqnarray}f=f_{\left[ \frac{2m+1}{2}\right]+1}+f_{\left[ \frac{2m+1}{2}\right]+2} \ldots + f_{n}\end{eqnarray}
と表すことができます。
これは、対称関数の一部であることから、対称性を説明することができました。
自己双対性について
自己双対関数の定義により、式(4)の変数及び関数\(f\)に否定を取ります。
\begin{aligned}f_{d}&=\overline{f_{\left[ \frac{2m+1}{2}\right]+1}(\overline{x_{1}},\overline{x_{2}},\ldots \overline{x_{n}})+f_{\left[ \frac{2m+1}{2}\right]+2}(\overline{x_{1}},\overline{x_{2}},\ldots \overline{x_{n}}) \ldots + f_{n}(\overline{x_{1}},\overline{x_{2}},\ldots \overline{x_{n}})} \\ &= \overline{f_{0}(x_{0},x_{1}\ldots x_{n})+f_{1}(x_{0},x_{1}\ldots x_{n})+f_{\left[ \frac{2m+1}{2}\right]}(x_{0},x_{1}\ldots x_{n})} \\ &= f_{\left[ \frac{2m+1}{2}\right]+1}(x_{0},x_{1}\ldots x_{n})+f_{\left[ \frac{2m+1}{2}\right]+2}(x_{0},x_{1}\ldots x_{n}) \ldots + f_{n}(x_{0},x_{1}\ldots x_{n}) \end{aligned}
以上の式変形で説明できました。
(3)対称関数と双対性
第2章により、ある関数\(f\)が対称関数であるとき、変数の個数によって出力0,1が決まる。((x,y,z)=(1,0,0),(0,1,0),(0,1,1)が異なる出力になることは無い。)
例として3変数対称関数を考える。
変数及び出力\(f\)の否定を取って双対関数を計算すると、下記の真理値表の対応になる。
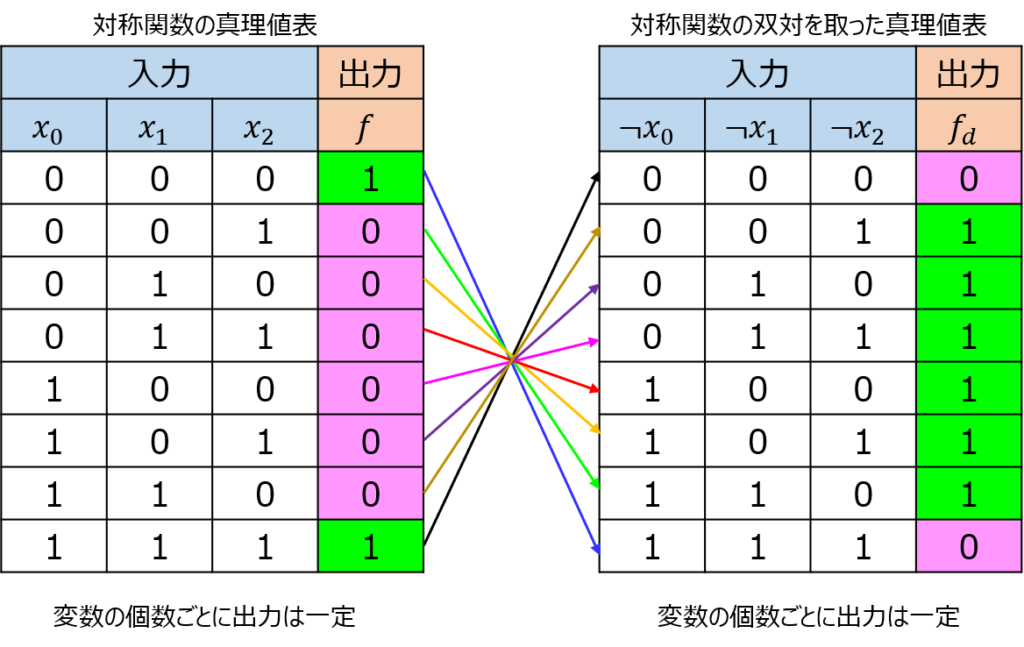
変数の否定を取り、元の対称関数に代入するため、真理値表が反転しただけで、対称性は保持される。
これが、任意のnに対して成立するため、題意は示された。
最後に
(3)は式で説明できるかもしれませんが、表で書いた方が分かりやすいと考え、上記の説明にしました。
問題が複雑になるほど、真理値表を書いて実験することが重要になります。
多数決関数は単調増大関数の性質もあります。合わせて確認しておきましょう。