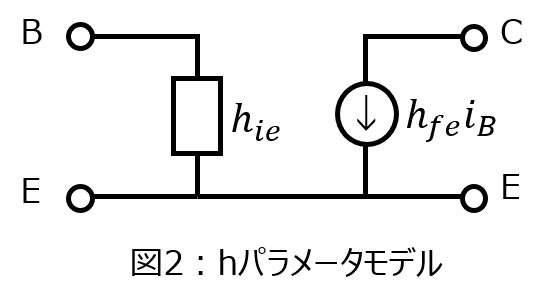
【問】バイポーラトランジスタを使用した以下のベース接地回路(図1)を考える。入力インピーダンス\(Z_{in}\)、出力インピーダンス\(Z_{o}\)、電圧利得\(K_{v}\)、電流利得\(K_{i}\)を求めよ。なお、微小信号等価回路を求めるときは、図2のhパラメータモデルを使用すること。
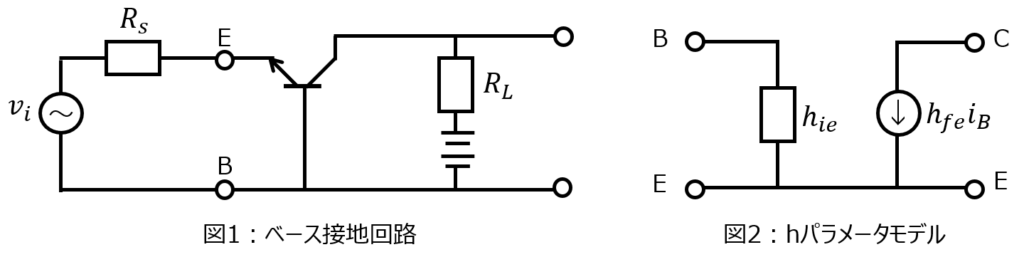
はじめに
バイポーラトランジスタの接地方式には、ベース接地、エミッタ接地、コレクタ接地の3パターンがあります。
それぞれの接地方式は、以下の特性であることがよく説明されています。

エミッタ接地、コレクタ接地方式の場合の導出は問題として良く出てきます。他サイトでもよく紹介されていますので、そちらを参照くださればと思います。
ベース接地については出題頻度が低いですが、微小信号等価回路にしたときに電圧源と電流源の入力側、出力側の電位が一致しないです。
見慣れない回路構成になるので、計算を流れ作業で行っていると面食らうことがあります。
本問では、微小信号等価回路の書き方とその後の利得の求め方の練習を、あえてベース接地で行いたいと思います。
微小信号等価回路の書き方
まず、バイポーラトランジスタ(BPP)周りの端子の位置を確認します。
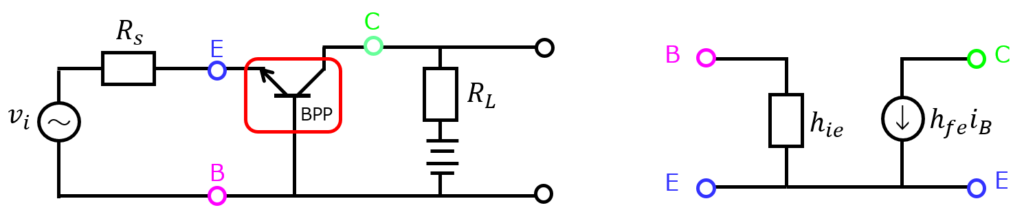
エミッタ(E)とコレクタ(C)が回路上段、ベース(B)が回路の下段にあることを確認します。
あとは、hパラメータモデルを確認し、端子の対応が合うように赤枠部分を置き換えます。
その結果、以下のように書き換えられます。
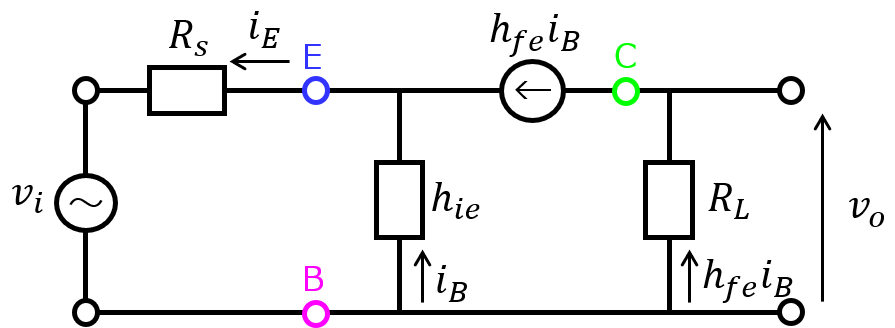
※ただし、\(i_{B}\)はベースに入力する電流。\(i_{E}\)はエミッタから出力する電流を表します。
電流の向きの設定は任意ですが、電流源からの出力の向きもあり、上記のように設定することが適切と考えました。
各パラメータの求め方
微小信号等価回路が書ければ、後は通常の電気回路と同じようにキルヒホッフの法則を立てます。
電流則:
\begin{eqnarray} i_{E}&=\left( 1+h_{fe}\right) i_{B}\end{eqnarray}
電圧則:
\begin{eqnarray} -v_{i}&=\left( 1+h_{fe}\right) i_{B}R_{s} \\ v_{0}&=-h_{fe}R_{L}i_{B}\end{eqnarray}
であるので、これを用いて各パラメータを求めていきます。
入力インピーダンス\(Z_{in}\):
\begin{eqnarray}Z_{in}&=\frac{v_{i}}{-i_{E}}&=\frac{\left( 1+h_{fe}\right) R_{s}i_{B}}{\left( 1+h_{fe}\right) i_{B}}&=\frac{\left( 1+h_{fe}\right) R_{s}}{\left( 1+h_{ie}\right) }&=R_{s}\end{eqnarray}
出力インピーダンス\(Z_{o}\):
\begin{eqnarray}Z_{o}=\frac{v_{0}}{-i_{0}}=\frac{h_{fe}i_{B}R_{2}}{h_{fe}i_{B}}=R_{L}\end{eqnarray}
電圧利得\(K_{v}\):
\begin{eqnarray}K_{v}=\frac{v_{o}}{v_{i}}=-\frac{h_{fe}R_{L}}{\left( 1+h_{fe}\right) R_{s}}\end{eqnarray}
電流利得\(K_{i}\):
\begin{eqnarray}K_{i}&=\frac{i_{o}}{i_{i}}&=\frac{i_{o}}{i_{E}}&=\frac{h_{fe}i_{B}}{\left( 1+h_{fe}\right) i_{B}}&=\frac{h_{fe}}{ 1+h_{fe}}\end{eqnarray}
と求めることができました。
入力端、出力端の取る場所で\(Z_{in}\)、\(Z_{o}\)の値が少し変わりますが、本記事では、回路の左端と右端がそれぞれ対応しています。
下記の参考文献では、エミッタ端とベース端から見た入力インピーダンスを求めていました。
(答えは、\(\frac{h_{ie}}{1+h_{fe}}\)になります。)
微小信号等価回路の問題を解く際は、どこの端子間の特性を問われているのか、注意深く問題文を読みましょう。
補足:ゲート接地回路
ベース接地回路と同様の接地方式として、MOSトランジスタのゲート接地回路があります。この特性を導出することもあります。
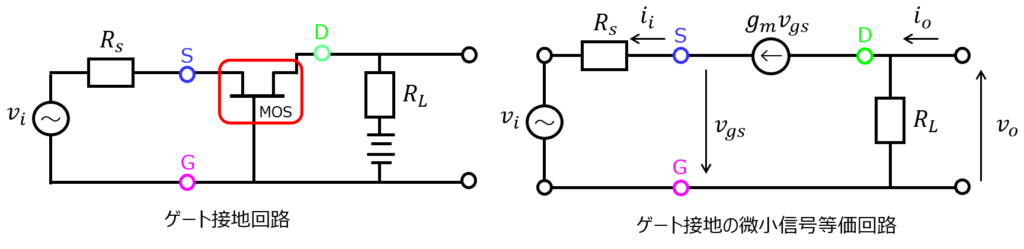
微小信号等価回路を書くと、右図のようになります。前章と同様にして、下記のように導出することができます。
\begin{cases}V_{i}=V_{s}=-V_{gs}-g_{m}v_{gs}\\ v_{0}=-R_{L}g_{m}v_{gs}\\ i_{i}=-g_{m}v_{gs}\\ i_{0}=i_{i}\end{cases}
入力インピーダンス\(Z_{in}\):
\begin{eqnarray}Z_{i}=\dfrac{v_{i} }{-i_{i}}=\dfrac{v_{gs}+g_{m}R_{s}v_{gs}}{g_{m}v_{gs}}=\dfrac{1+g_{m}R_{s}}{g_{m}}\end{eqnarray}
出力インピーダンス\(Z_{o}\):
\begin{eqnarray}Z_{o}=\dfrac{v_{o}}{i_{o}}=R_{L}\end{eqnarray}
電圧利得\(K_{v}\):
\begin{eqnarray}K_{v}=\dfrac{R_{L}g_{m}v_{gs}}{v_{gs}+g_{m}v_{gs}R_{s}}=\dfrac{R_{L}g_{m}}{1+g_{m}R_{s}}\end{eqnarray}
電流利得\(K_{i}\)は、\(i_{i}=i_{o}\)により、\(K_{i}=1\)
式(4)~(7)と比較すると、ベース接地回路と類似の特性になるパラメータが多いことが分かりました。
最後に
微小信号等価回路を書いて、問題で求められているパラメータを求める問題は、電子回路の超頻出分野です。
今後、複雑な電子回路を扱い、その時のパラメータの算出方法の紹介も行いますので、まずは本記事で解き方の基本を押さえていただければと思います。
参考文献
樋口 龍雄 (著), 江刺 正喜 (著):電子情報回路 I P78