はじめに
今までの記事で、オペアンプには様々な使われ方があることを説明してきました。(発振回路、比較器、A-D変換など)
まだまだ他の使い方はありますので、本記事でも引き続き紹介していきます。
オペアンプは、足し算、引き算の使い方をすることができます。
前提には反転増幅回路の知識が必要なので、ここから説明していきます。
反転増幅回路とは
下記の回路構成を言います。+端子を接地し、帰還回路\(Z_{2}\)で、-端子と出力端子を接続して構成している負帰還回路です。
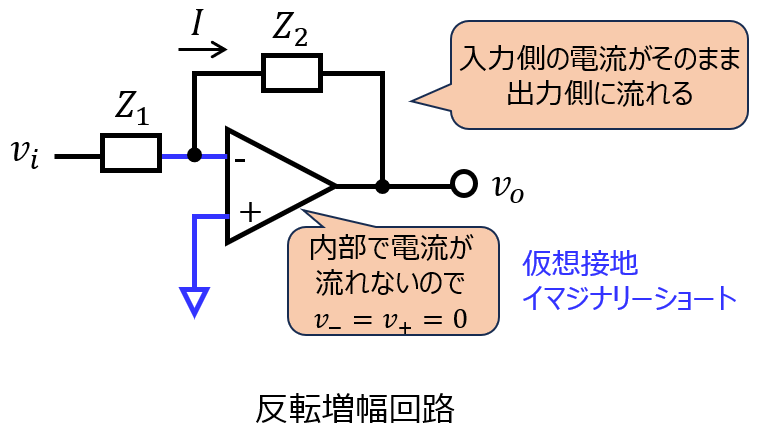
利得\(A\)が有限の場合で考えることもありますが、今回はオペアンプが理想的とし、\(A=∞\)で考えることにします。
このとき、オペアンプの内部抵抗は∞のため、-から+へ電流が流れないと考えられます。
電流が流れないと、電位差も発生しないので、オペアンプの+極にかかっている接地条件がそのまま+極にも来ます。(仮想接地:イマジナリーショートとも言います。)
+極の電位は0なので、下記の回路方程式が立ちます。
\begin{cases}v_{i}=Z_{1}I \\ v_{o}=-Z_{2}I\end{cases}
これを解くと、出力電圧は
\begin{aligned}v_{o}=-\dfrac{R_{2}}{R_{1}}v_{i}\)\end{aligned}
であることが分かります。
“反転”なので、出力の符号は逆になっていますが、絶対値としてみると電圧が抵抗値の比の分増幅していることが分かります。
加減算は、この性質を利用します。
オペアンプを利用した加算回路
下記の図を考えます。先ほどの章と比較して、抵抗\(R_{1}\)と並列に、抵抗\(R_{2}\)も接続しています。
入力電圧\(v_{1},v_{2}\)を足して、出力電圧\(v_{o}\)を計算することを考えます。
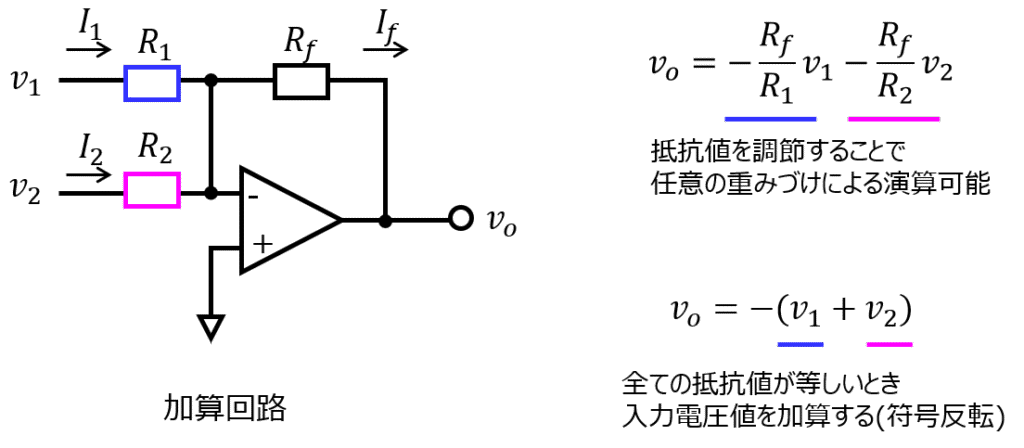
(2)式を用いて、\(v_{1}\)と\(v_{2}\)の入力分それぞれ重ね合わせ、出力電圧\(v_{o}\)を求めます。
\begin{aligned}v_{o}=v_{o}=-\dfrac{R_{f}}{R_{1}}v_{1}-\dfrac{R_{f}}{R_{2}}v_{2}\end{aligned}
と、抵抗値を調整することで、それぞれの入力電圧\(v_{1},v_{2}\)に対し、任意の重みづけをして加算できます。
(反転増幅回路の都合上、符号が逆転しています。+に戻した方が、分かりやすいかもしれません。)
重みづけの必要が無いときは、\(R_{1}=R_{2}=R_{f}\)とし
\begin{aligned}v_{o}=-(v_{1}+v_{2}end{aligned}
とできるため、入力電圧分を単に加算した値が出力として出ます。
オペアンプを利用した減算回路(差動増幅回路)
加算回路と逆です。オペアンプのマイナス側に抵抗を設定します。
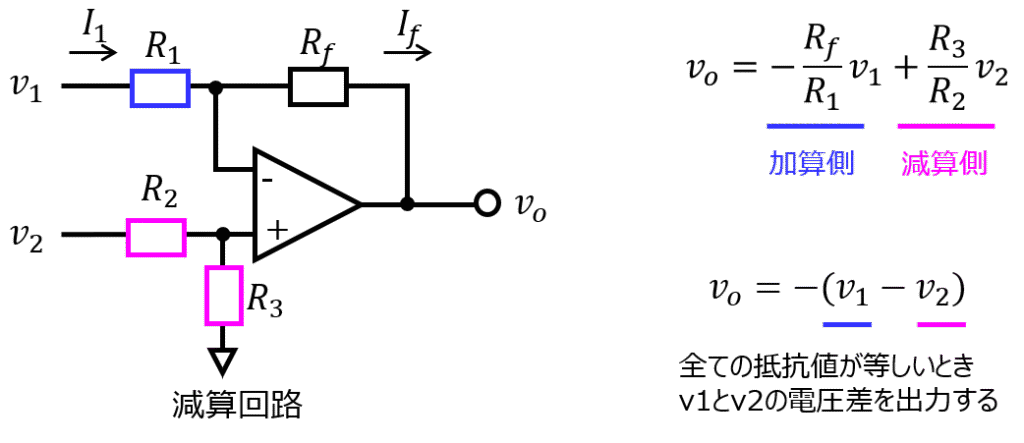
青字で書いた抵抗\(R_{1}\)は加算回路と同じです。
ピンク色で書いた抵抗\(R_{2},R_{3}\)に注目します。
このとき、オペアンプの+側の電圧\(v_{+}\)は加算回路のように0になりません。
分圧則により、オペアンプの+側の電圧\(v_{+}\)は、
\begin{aligned} v_{+}=\dfrac{R_{3}}{R_{2}+R_{3}}v_{2} \\ v_{-}=\dfrac{R_{f}v_{1}+R_{1}v_{o}}{R_{1}+R_{f}} \end{aligned}
仮想接地条件より、\(v_{+}=v_{-}\)を利用して
\begin{aligned}v_{o}=\dfrac{R_{1}+R_{f}}{R_{1}}\left(\dfrac{R_{3}}{R_{2}+R_{3}}v_{2}-\dfrac{R_{f}}{R_{1}+R_{f}}v_{1}\right)\end{aligned}
と、\(v_{1}\)から\(v_{2}\)を差し引いた分増幅できていることが分かります。
なお、教科書によっては下記の関係を利用して、上式を簡略化することがあります。
\(\dfrac{R_{f}}{R_{1}}=\dfrac{R_{3}}{R_{2}}\)より
\begin{aligned}v_{o}=-\dfrac{R_{3}}{R_{2}}(v_{1}-v_{2})=-\dfrac{R_{f}}{R_{1}}v_{1}–\dfrac{R_{3}}{R_{2}}v_{2}\end{aligned}
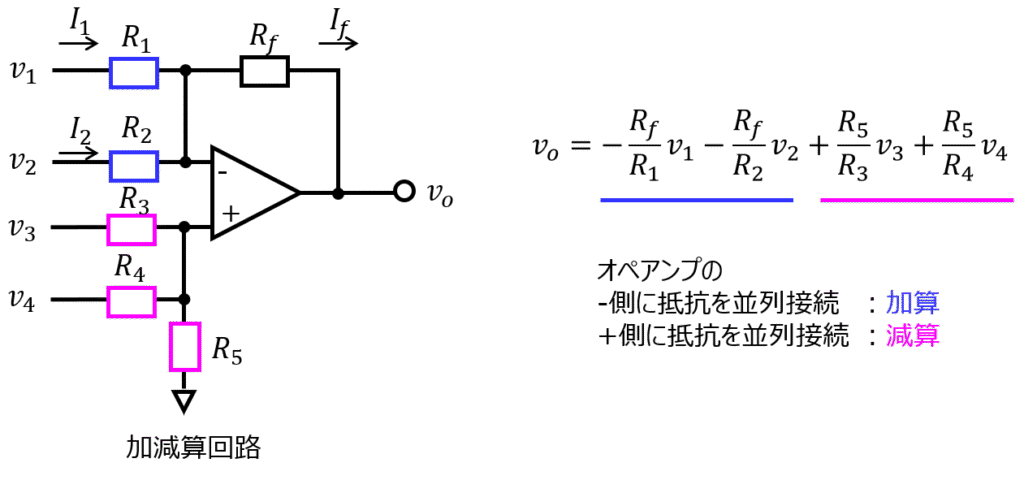
加減算回路
加算回路、減算回路を合わせて、加算減算回路を作成できます。
オペアンプの-側に加算したい電圧、+側に減算したい電圧源を接続し、抵抗による重みづけを行います。
最後に
加算回路、減算回路は、動作原理の説明自体は問われないことが多いものの、出力電圧の計算など、院試で出題されることもあります。
本記事では、回路計算も含めて動作を説明してきました。
網羅的な理解に繋がると幸いです。