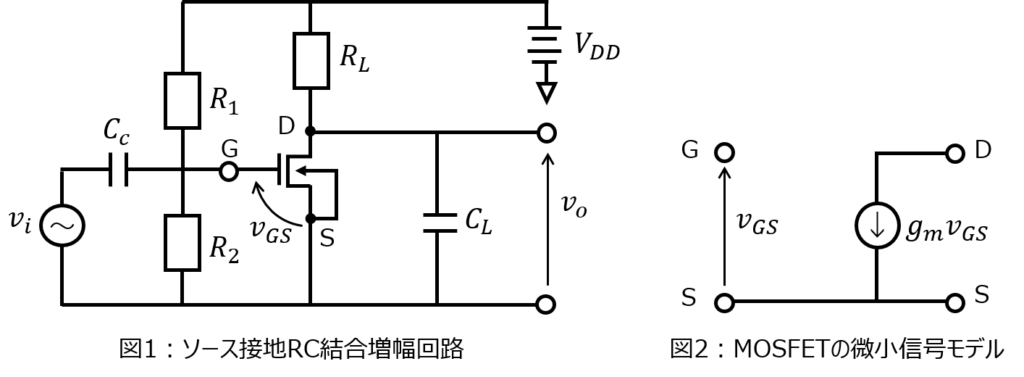
下記の図1に、MOSFETを用いたソース接地RC交流増幅回路を示す。
(1)図2の微小信号モデルを用いて、図1の微小信号等価回路を示せ。
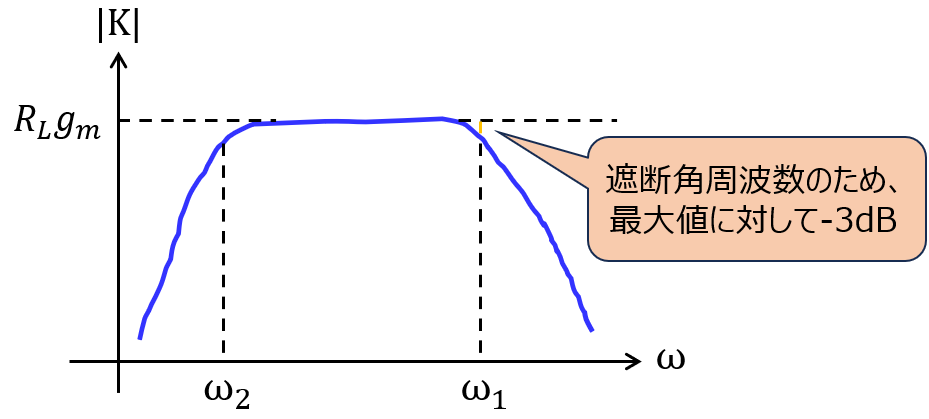
(2)電圧利得\(K=\dfrac{v_{o}}{v_{i}}\)を求めよ。また、電圧利得の振幅|K|と角周波数\(\omega\)の関係の概略を図示せよ。このとき、低域遮断周波数\(\omega_{l}\)及び高域遮断周波数\(\omega_{h}\)を求めよ。また、中域周波数帯での電圧利得\(|K_{o}|\)を求めよ。
MOSFETとは
金属半導体電界効果トランジスタの英訳です。(Metal-Oxide-Semiconductor Field-Effect Transistor)
以前の記事で動作原理を詳しく紹介していますが、平たく言えば増幅器の一つです。ゲートに電圧をかけて、増幅の有無を切り替えます。(電圧をかけているとき、増幅可能)
ゲートに電圧をかけているとき、ドレインからソースに電流が流れると、出力端側には入力端以上の電圧が流れ、出力電圧が入力電圧以上に大きくなります。
本記事では、これを電子回路の観点で見ていきます。
微小信号等価回路の書き方
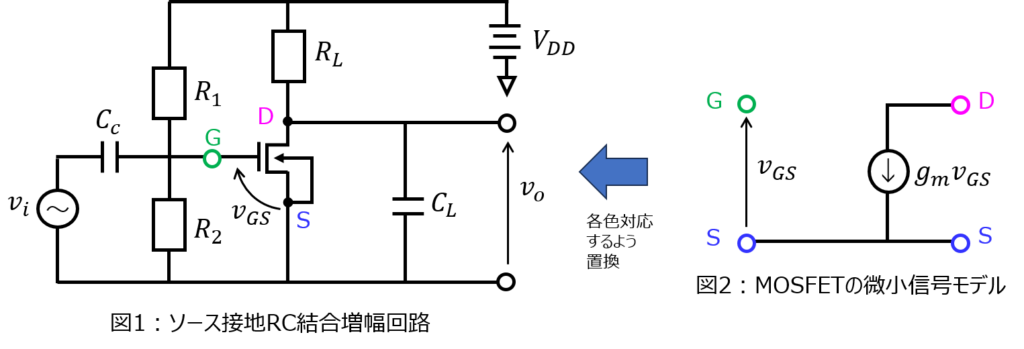
これも、過去の記事で詳しく説明しています。図1の回路では、MOSFETの記号シンボルがブラックボックスで回路方程式を立てることができません。
これを、図2にある微小信号モデルを用いて、ゲート、ソース、ドレインの位置が図1と合うように置き換えます。
電圧利得と周波数特性
(2)の計算を進めていくと
角周波数を変数とした電圧利得\(K(\omega)\)が下記の形で表されます。
\begin{aligned}K=\dfrac{A}{\left( 1+j\dfrac{\omega }{\omega_{1}}\right) \left( 1-j\dfrac{\omega_{2}}{\omega }\right)} \end{aligned}
利得は下記の概形になります。ただし、\((\omega_{1}>\omega_{2})\)
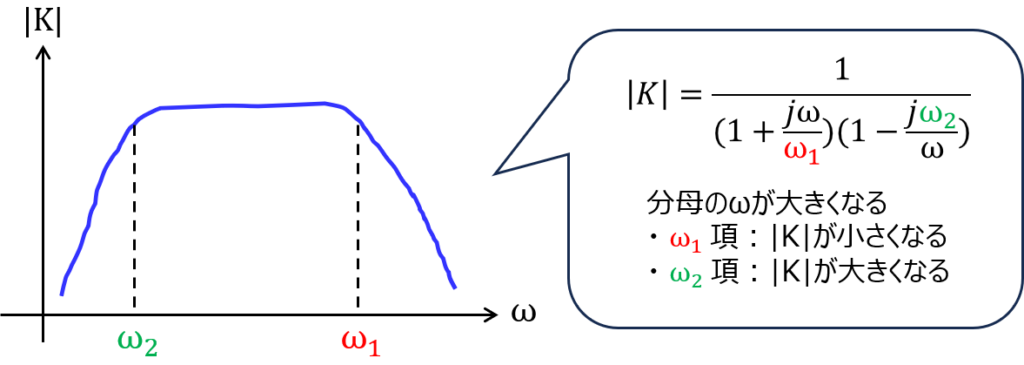
これは、角周波数を0から大きくするとどうなるかイメージすると分かりやすいです。
\(\omega=0\)のとき、分母の\(\omega_{2}\)に関わる項が発散し、∞になります。分子は有限な値なので、利得は0になります。
ここから\(\omega\)を大きくしていくと、やがて\(\omega_{2}\)の項が有限な値になります。すると、利得も0より大きい値となるため、上昇傾向になることがわかります。
\(\omega\)が\(\omega_{2}\)より大きい値になると、\(\omega_{2}\)の項は0に近似できます。よって、\(\left( 1+j\dfrac{\omega_{2}}{\omega }\right)\)の第2項は無視でき、1になります。
これと逆のことが\(\omega_{1}\)の項に対して起こります。今度は、変数\(\omega\)が分子にあるので、\(\omega\)が非常に大きくなると、利得が0になるということですね。
問題の都合で、虚部の符号は正と負をそれぞれ付けましたが、逆だったとしても結果は変わりません。
解答例
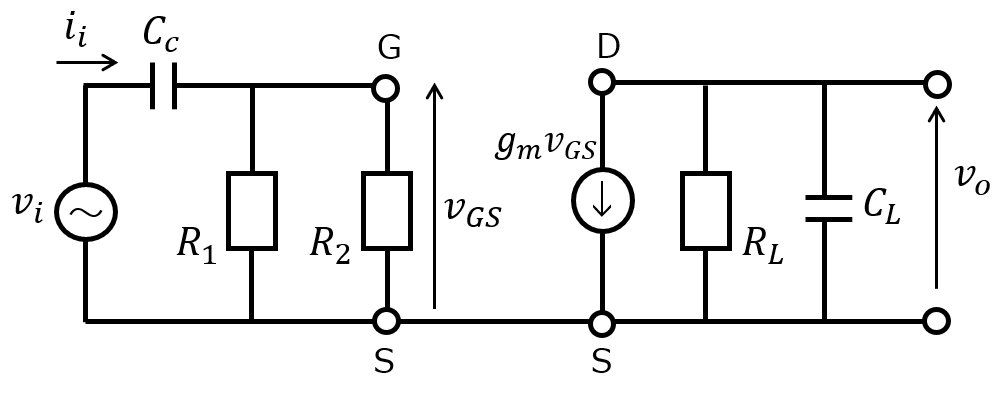
(1)微小信号等価回路
分かりやすくするため、ゲート、ソース、ドレインそれぞれに色を付けました。
直流電流源\(V_{DD}\)に繋がるラインは電圧0。すなわち、(\(v_{i},v_{o})\)の負側と同じ電位にできるので、下記のようになる。
(2)周波数特性
微小信号等価回路より、入力端からの電流\(i_{i}\)を設定すると下記のようになる。
\begin{aligned}i_{i}=\dfrac{v_{GS}}{R_{1}}+\dfrac{v_{GS}}{R_{2}}= \dfrac{R_{1}+R_{2}}{R_{1}R_{2}}v_{GS}\end{aligned}
コンデンサ\(C_{c}\)分の電圧降下を合わせると、入力電圧は
\begin{aligned}v_{i}=\left( \dfrac{1}{j\omega C_{c}}\cdot \dfrac{R_{1}+R_{2}}{R_{1}R_{2}}+1\right) v_{GS}\end{aligned}
抵抗\(R_{L}\)、コンデンサ\(C_{L}\)の合成インピーダンス\(Z\)は
\begin{aligned}Z=\dfrac{\dfrac{R_{L}}{j\omega C_{L}}}{R_{L}+\dfrac{1}{j\omega C_{L}}}=\dfrac{R_{L}}{1+j\omega C_{L}R_{L}}\end{aligned}
これより、出力電圧\(v_{o}\)は
\begin{aligned}v_{o}=-Zg_{m}v_{GS}=-g_{m}v_{GS}\dfrac{\dfrac{R_{L}}{j\omega C_{L}}}{R_{L}+\dfrac{1}{j\omega C_{L}}}=\dfrac{R_{L}}{1+j\omega C_{L}R_{L}}\end{aligned}
これより、電圧利得は
\begin{aligned}K=\dfrac{v_{o}}{v_{i}}&=\dfrac{-\dfrac{R_{L}}{j\omega C}g_{m}}{\left( R_{1}+\dfrac{1}{j\omega C}\right) \left( 1+\dfrac{R_{1}+R_{2}}{j\omega CR_{1}R_{2}}\right) } \\ &= \dfrac{-R_{L}g_{m}}{\left( 1+j\omega C_{L}R_{L}\right) \left( 1-j\dfrac{R_{1}+R_{2}}{\omega C_{L}R_{1}R_{2}}\right) }\end{aligned}
\(\omega_{1}=\dfrac{1}{C_{L}R_{L}},\omega_{2}=\dfrac{R_{1}+R_{2}}{C_{c}R_{1}R_{2}}\)とすると、下記の周波数特性になる。
最後に
回路の形は変わることがありますが、電子回路の利得を求め、周波数特性を図示する問題は院試頻出です。是非、本問で練習してみると良いです。


