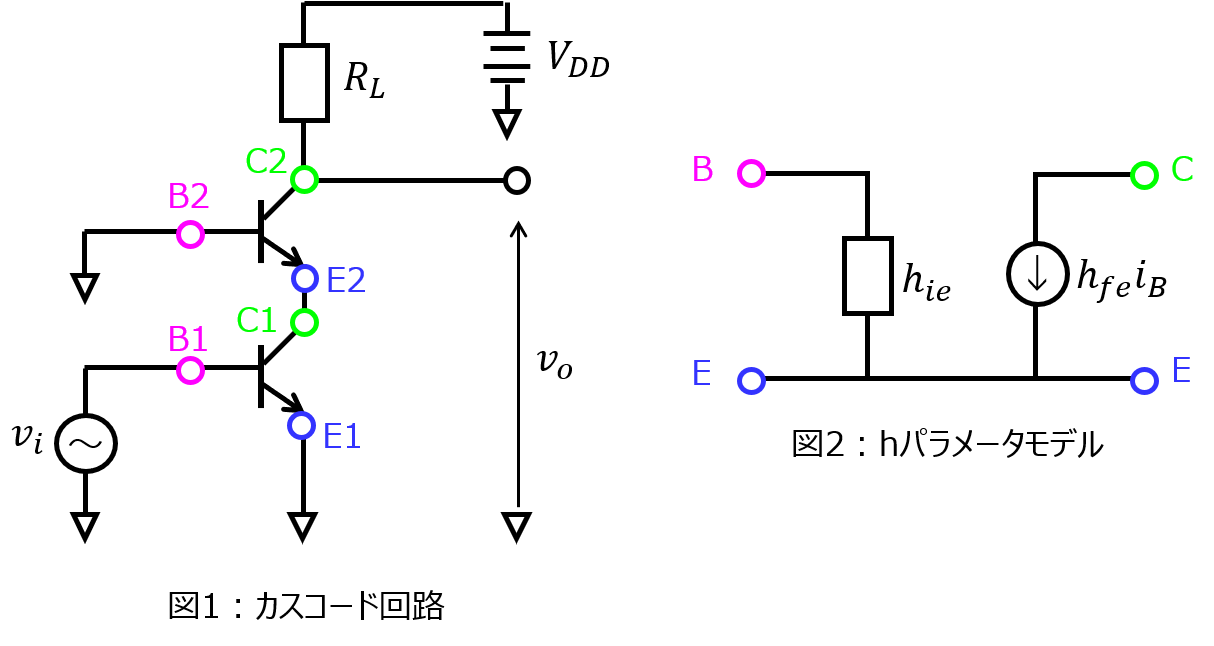
下記のカスコード回路を考える。
(1)微小信号等価回路を示せ。
(2)この回路の電圧利得を求めよ。
(3)トランジスタが一つの場合と比較して、カスコード回路の電圧利得を比較するとともに利点を述べよ。
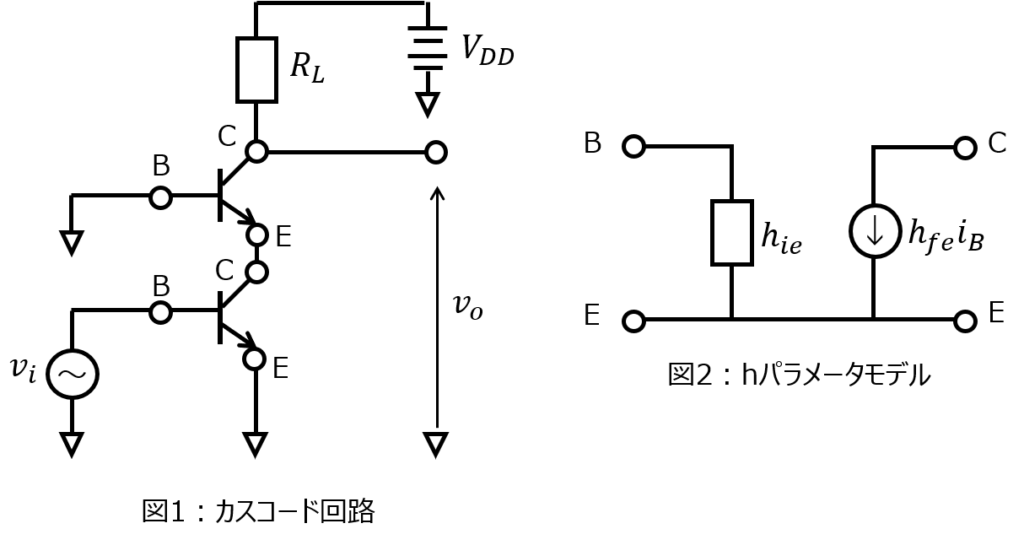
カスコード回路とは
トランジスタを2つ直列に接続した回路です。ベースを接地し、下段のトランジスタに電圧を入力するのが特徴です。
2つ直列に接続していることから、1つだけの場合と比較して電圧利得が大きい・・・と考えますでしょうか。
実は、利得は微減します。ですが、メリットもあります。(3)で詳細に見ていきます。
なお、上段の回路に電圧を入力したときは、ダーリントン回路になります。
解答例
(1)微小信号等価回路
今まで紹介してきた記事と同じです。
ただ、トランジスタが2つあり、接地されている箇所が違います。
これに気を付けてhパラメータを当てはめていくと、以下のようになります。
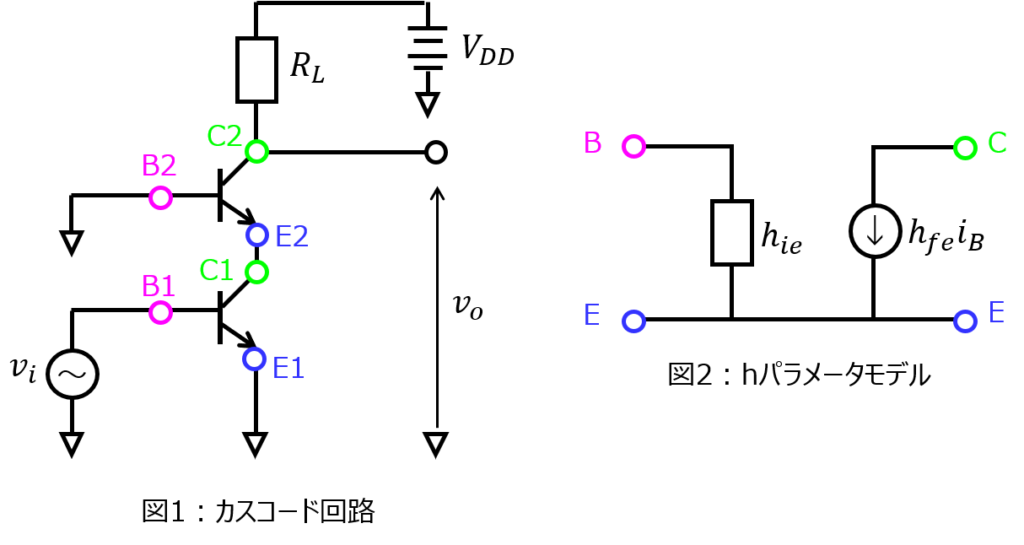
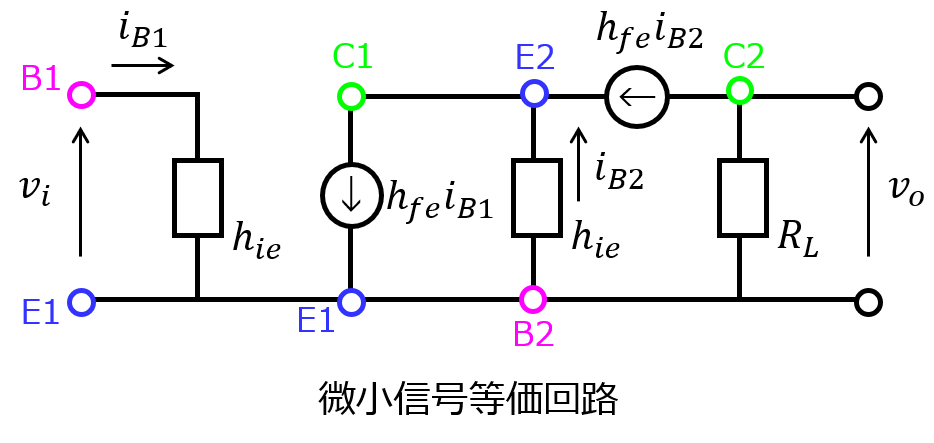
上記の回路を元に、(2)以降を考えていきます。
(2)電圧利得
回路方程式より
\begin{cases}v_{in}=h_{ie}i_{B1} \\ v_{o}=-h_{fe}R_{L}i_{B2} \\ h_{fe}i_{B1}=h_{fe}i_{B2}+i_{B2}\end{cases}
これより、\begin{aligned}v_{o}=-\dfrac{h_{fe}^{2}}{h_{fe}+1}R_{L}i_{B1}\end{aligned}
以上より、求める電圧利得は
\begin{aligned}K=\dfrac{v_{o}}{v_{i}}=-\dfrac{R_{L}h_{fe}^{2}}{h_{ie}(h_{fe}+1)}=-\dfrac{R_{L}h_{fe}}{h_{ie}}\dfrac{1}{1+\frac{1}{h_{fe}}}\end{aligned}
(3)カスコード回路の利点
トランジスタが一つのとき、下記の回路方程式になる。
\begin{cases}v_{in}=h_{ie}i_{B} \\ v_{o}=-h_{fe}R_{L}i_{B}\end{cases}
以上より、求める電圧利得は
\begin{aligned}K=-\dfrac{R_{L}h_{fe}}{h_{ie}}\end{aligned}
エミッタ接地だと、\(h_{fe}\)は50程度です。
(3)式に代入すると、(5)式に対して0.98倍になります。微減するものの、殆ど同じと見て良いです。
2段目のエミッタ接地で得られる利得の一部を失うものの、代わりに、1段目のベース接地特有のメリットを得ることができます。
ミラー効果を低減し、入出力間の容量が小さくなるので、高周波の増幅に有利になります。
ミラー効果とは
エミッタ接地のように、利得が大きい回路構成にしたときに起こる現象です。
高周波電源を入力したときの電圧利得が低下します。
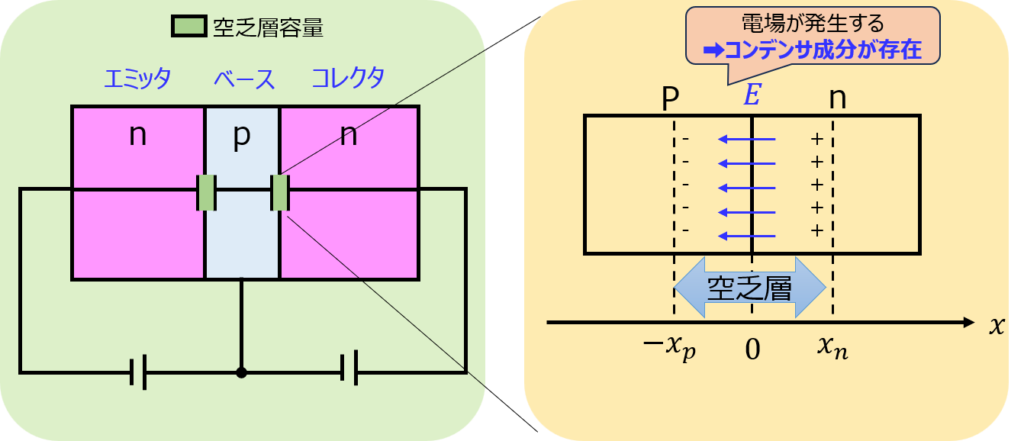
イメージ論ですが、npnバイポーラトランジスタの 図を今一度思いだしましょう。
n-p-n型半導体を3つサンドイッチ状に接続しています。こうなると、どうなるでしょうか。
異なる半導体界面で空乏層が発生し、拡散電場が発生します。
電場が発生すると、コンデンサ成分が発生していると解釈できます。
特に、コレクタ-ベース間の容量が高周波特性に大きな影響を及ぼします。(エミッタ接地のように利得が大きい回路の場合)
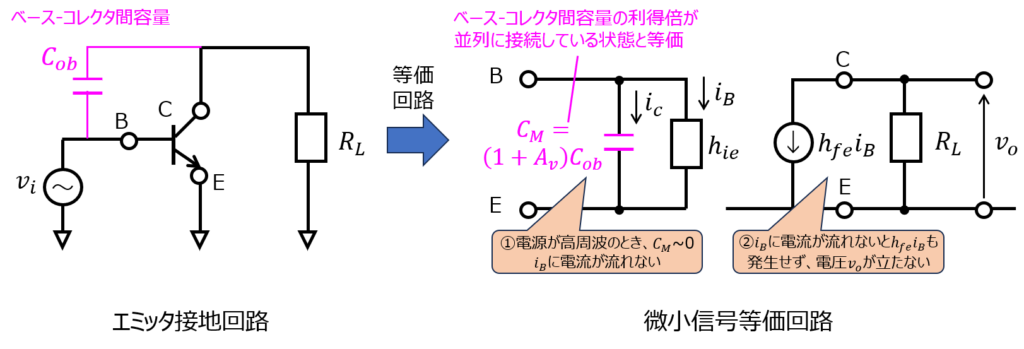
等価回路電圧利得を\(K_{v}\)とすると、
\begin{aligned}i_{cb}=v_{ob} \cdot j \omega C_{ob} \\ v_{ob}=v_{i}-v_{c} \\ v_{c}=-A_{v}v_{i}\end{aligned}
これより、
\begin{aligned}\dfrac{i_{cb}}{v_{i}}=j \omega(1+A_{v})C_{ob}=j \omega C_{M}\end{aligned}
\begin{aligned}C_{M}=(1+A_{v})C_{ob}\end{aligned}
とコレクタ-ベース間の容量が利得分大きくなって、入力側に並列接続されているように見えます。これをミラー容量と言います。
高周波になるにつれて、\(C_{M}\)にばかり電流が流れ、\(i_{b}\)にはあまり電流が流れなくなります。
その結果、\(h_{fe}i_{b}\)の電流も小さくなり、出力電圧が小さくなります。これにより、利得が小さくなってしまうことが分かりました。
ベース接地と組み合わせることで、周波数特性が改善する
前節のように、エミッタ接地でトランジスタ回路を構成すると、高周波電圧印加時の利得が下がってしまうことが分かりました。
しかし、ベース接地と組み合わせることで、利得が出る周波数帯域が広がります。
これは、小信号等価回路で考えると分かりやすいです。
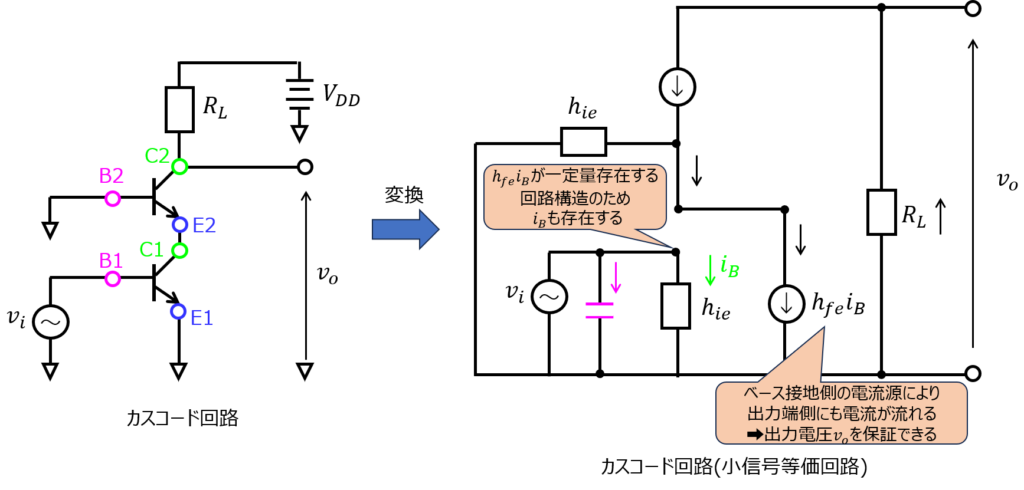
2段目をベース接地していると、1段目のエミッタと同電位になり、電流が還流することが分かります。
その結果、高周波を流し、\(h_{ie}\)に電流が流れず、コンデンサ\(C_{M}\)に電流が流れたとしても、2段目のベースから1段目のコレクタへ電流が戻ります。
電圧源は固定であることから、一部は\(h_{ie}\)に電流が流れることで、\(i_{b}\)が担保されます。
その結果、出力端側の\(h_{fe}i_{B}\)も立ちますので、出力電圧\(v_{o}=R_{L}h_{fe}i_{B}\)も立ちます。
よって、高周波数帯でも利得が出ます。
最後に
類題が北大で出題されたことがあります。同大学を志望する方は是非チェックしてください。
また、ミラー効果は、他サイトではオペアンプモデルで説明していることが殆どです。
しかし本問は、トランジスタの問題ですので、トランジスタモデルに拘り説明をしました。文献も少ないため、拙い部分がある場合は、大変申し訳ございません。
また、問題の時点からコンデンサ成分\(C_{M}\)を利用して解くこともできたかもしれませんが、試験問題としてそのような問われ方をした問題がありません。(試験時間的にも計算に時間がかかってしまうと思います。)
\(C_{M}\)は、理解を助ける概念として持っておいて、実際に問題を解くときは、与えられたモデルを用いて解く方が良いと思います。