オペアンプを用いたRC発振回路の例と特徴

問題

(1)RC発振回路の特徴と欠点を述べよ。

(2)下記にRC移相型発振回路及びウィーンブリッジ発振回路を示す。入力電圧を\(v_{1}\)、出力電圧を\(v_{2}\)とする。
それぞれのループ利得\(\dfrac{v_{2}}{v_{1}}\)から、発振条件(振幅条件、周波数条件)を求めよ。ただし、オペアンプの増幅率は理想的とする。

はじめに
RC発振回路とは
解答例
最後に

はじめに

以前の記事で、オペアンプを利用した回路の発振条件について説明してきました。今回はその続きでRC発振回路の発振条件について考えていきます。

特に九大で頻出ですので、受ける方は是非チェックすると良いです。

RC発振回路とは

オペアンプの帰還部分が抵抗とコンデンサにより構成される発振回路を言います。

コイルや水晶振動子を用いないため低周波での発振が容易です。

しかし、その反面ひずみが生じやすいです。また、発振周波数の安定性もあまり高くない欠点もあります。

RC発振回路においてひずみを少なくするためには、ループ利得を限りなく1に近づける必要があります。

これを、下記のRC移相型発振回路、ウィーンブリッジ発振回路でどのように実現していくか、見ていきます。

お詫び (24/10/28追記)

24/10/27までは、オペアンプの負帰還にRとCを並列接続したローパスフィルタ型回路(1段)の図を本章に記載していました。

後段の説明をしやすくするための簡易的なイメージ(概念)として提示していました。しかし、この回路は実際には発振しません。

このため、本記事から該当の図を削除いたしました。皆様に誤解を与えてしまったこと、深くお詫び申し上げます。

解答例

RC発振回路の特徴については前章に述べた通り、以下でループ利得を計算する。

RC移相型発振回路

下記のように、オペアンプの帰還部分にコンデンサと抵抗が並列(多段)に繋がった回路を言います。

C-Rを3段以上縦続接続しており、C一つに付き位相が-90度に漸近して遅れるので、3段あれば180度以上回転させることが可能です。

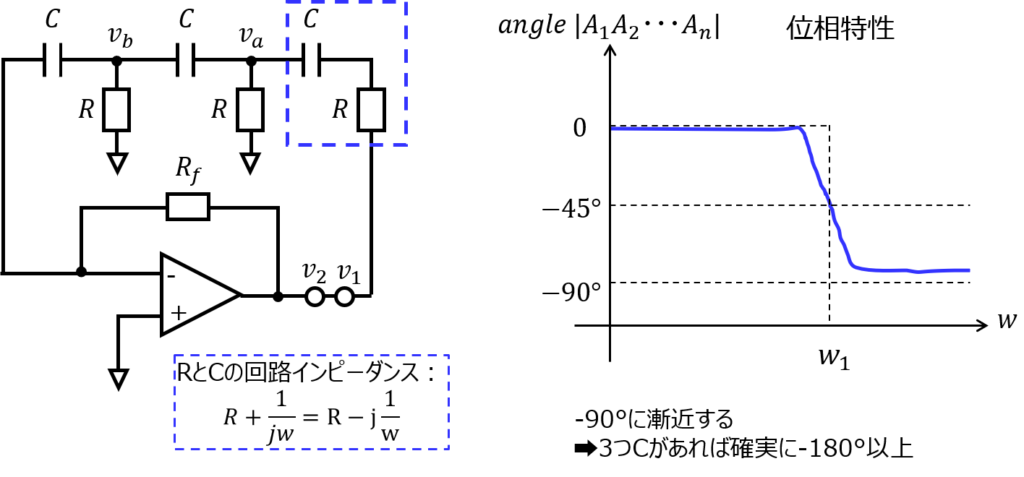
下記の回路方程式を利用し、ループ利得を計算します。

\begin{cases}\dfrac{1}{R+\frac{1}{j \omega C}}(v_{1}-v_{a})=\dfrac{v_{a}}{R}+j \omega C (v_{a}-v_{b}) \\ j \omega C (v_{a}-v_{b})=\dfrac{v_{b}}{R}+j \omega C v_{b} \\ j \omega C v_{b}= – \dfrac{v_{2}}{R_{f}}\end{cases}

上式を連立し、ループ利得\(AH\)は

\begin{aligned}AH=\dfrac{v_{2}}{v_{1}}=\dfrac{1}{-\frac{R}{R_{f}}+\frac{5}{\omega^{2}C^{2}RR_{f}}+j\left( \frac{6}{\omega C R_{f}}-\frac{1}{\omega^{3}C^{3}R^{2}R_{f}}\right)}\end{aligned}

ひずみを少なくするためには、ループ利得を限りなく1に近づける必要があります。

可変抵抗\(R_{f}\)を用いて、定抵抗\(R\)と下記の関係を実現します。\begin{aligned} R_{f}≧29R \end{aligned}

ここで、\(R_{f}\)にサーミスタを用いると良いです。

なぜならば、サーミスタは、温度が上昇すると抵抗値が下がる性質があるからです。

発振条件で、ループ利得が大きくなると、出力電圧も大きくなり、電流も大きくなります。
すると、サーミスタの温度上昇が発生し、抵抗値が下がる　→　\(v_{2}\)が下がる　→　ループ利得が低下する負帰還がかかり、発振振幅を小さくできます。

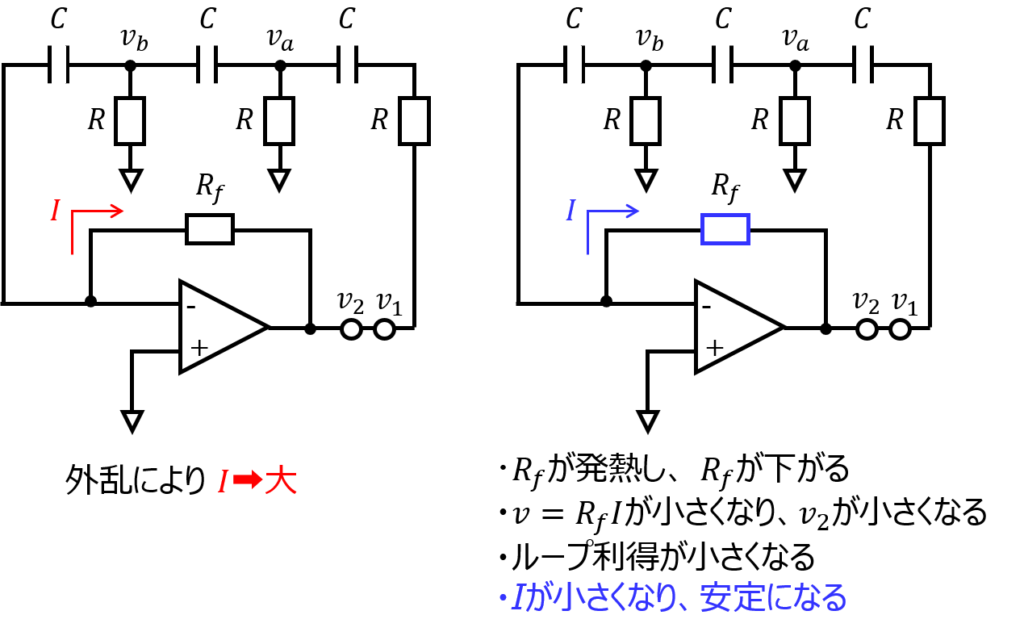
このような動作原理にて、一定振幅をひずみ少なく実現することができます。

ウィーンブリッジ発振回路

オペアンプの帰還部分が抵抗とコンデンサによって構成される回路のうち、オペアンプの-側に抵抗が接続されているものを指します。

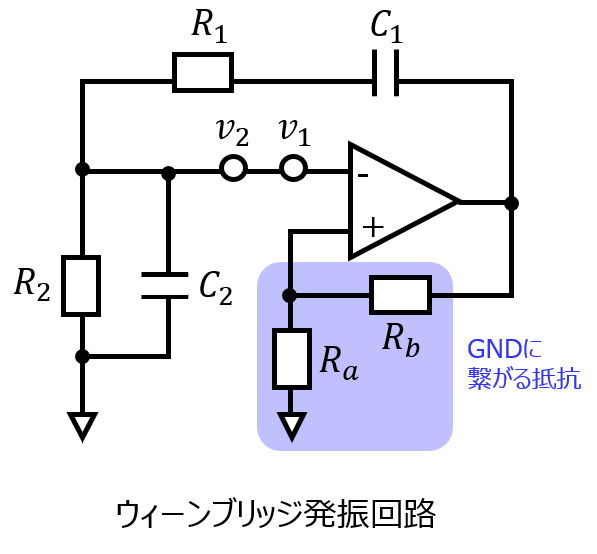
増幅率は∞なので、オペアンプの-側、+側それぞれにかかる電圧の関係は

\begin{aligned}v_{-}=v_{+}\end{aligned}

分圧則から

\begin{cases}v_{-}=\dfrac{R_{a}}{R_{a}+R_{b}}v_{o} \\ v_{2}=\dfrac{\frac{R_{2}}{1+j \omega C_{2}R_{2}}} {R_{1}+\frac{1}{j \omega C_{1}}+\frac{R_{2}}{1+j \omega C_{2}R_{2}}}v_{o} \end{cases}

第二式を簡単にして

\begin{aligned}v_{2}=\dfrac{j \omega C_{1} R_{2}}{j \omega C_{1}(R_{1}+R_{2})+1+j \omega C_{2}R_{2}- \omega^{2}C_{1}C_{2}R_{1}R_{2}}\end{aligned}

まず、周波数条件について考える。(3)式の虚部が0であることに注目する。分子が虚数なので、分母の実部が0になれば条件を満たせる。

\begin{aligned}1-\omega^{2}C_{1}C_{2}R_{1}R_{2}=0 \\ \omega=\dfrac{1}{\sqrt{C_{1}C_{2}R_{1}R_{2}}}\end{aligned}

次に、振幅条件について、ループ利得\(\dfrac{v_{2}}{v_{1}}\)は、(2)の第一式を利用して

\begin{aligned}&\dfrac{v_{2}}{v_{1}}=\dfrac{R_{a}+R_{b}}{R_{a}}\dfrac{C_{1}R_{2}}{C_{1}R_{1}+C_{1}R_{2}+C_{2}R_{2}}≧1 \\ &1+\dfrac{R_{b}}{R_{a}} ≧ 1+\dfrac{R_{1}}{R_{2}}+\dfrac{C_{2}}{C_{1}} \end{aligned}