【制御工学】定常偏差の求め方

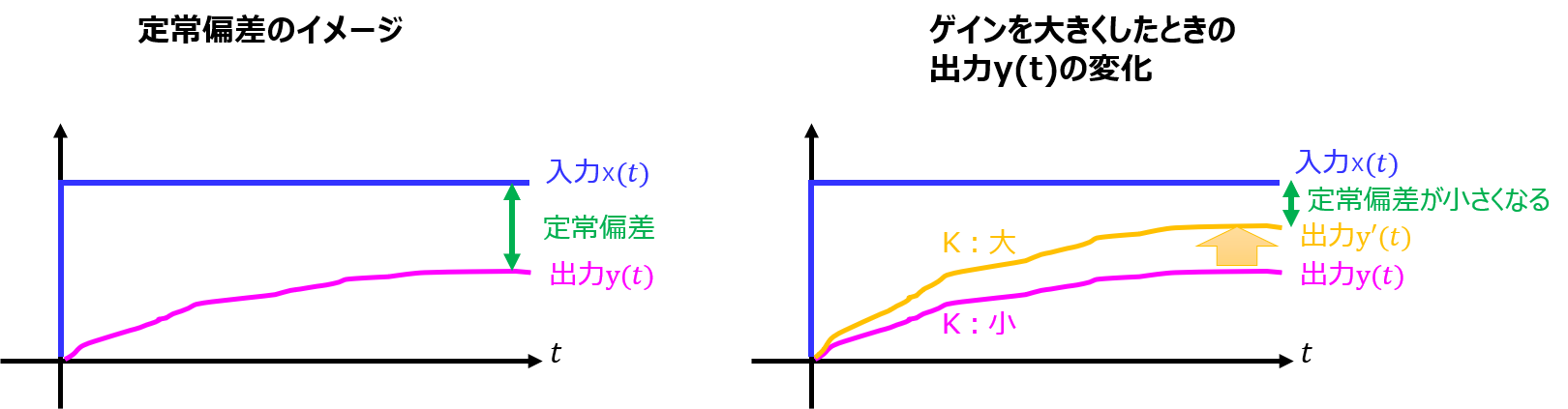
下記のような制御系を考える。伝達関数\(G\left( s\right) =\dfrac{s+\sqrt{3}}{\left( s+1\right) ^{2}}e^{-Ls}\)で与えられる。ここで、\(L>0\)である。図(b)は、図(a)の系において\(G(s)\)の前にゲイン要素\(K>0\)を挿入したものである。次の問いに答えよ。

(6)図(b)において、位相交差周波数\(\omega_{\pi}=\sqrt{3}\)とする。目標値が単位ステップ関数である時の定常偏差をKで表せ。
(7)(6)の条件においてKを大きくすると、定常偏差は小さくなるが安定性が悪くなる。安定性を損なわないεの下限を求めよ。

東北大学 電気情報系 院試 2014年8月 専門科目(電気工学) から引用 一部記載を修正

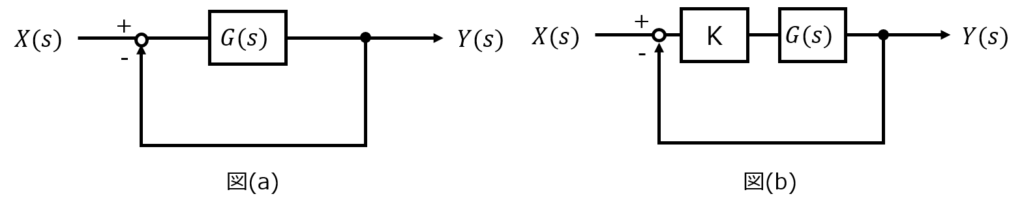
はじめに

本問は、前回の記事の続きです。(5)以前の問題を解説しています。

今までは、ある制御系の安定性を定量的に評価してきました。本記事では、ゲインを大きくしたとき、応答性、偏差は小さくなるが、安定性が損なわれることを院試問題を通して見ていきます。

定常偏差とは

ある制御系に入力を与え、定常状態になったとき、入力に対する出力値の差分を言います。

例えば、入力1を与えて、最終的な出力が0.5になったとき、定常偏差は1-0.5=0.5になります。

ゲインを大きくすると、偏差が0.5より小さくなりますが、安定性が損なわれます。

これは、伝達関数の形からも考えることができます。

ゲインを変化させたときの安定性の変化

例として、開ループ伝達関数\(G\left( s\right) =\dfrac{K}{s\left( s+1\right) \left( s+2\right) }\)を考えます。

この伝達関数の極は、特性方程式\(1+G(s)=0\)より

\begin{eqnarray}s^{3}+2s^{2}+2s+K=0\end{eqnarray}

文字Kのまま求めてしまうと、大変複雑な解になりますので、ここではK=0,1,10,100…と代表的なパラメータを割り振り、その時の極を見ていきます。

wolfram alphaで計算すると以下のようになります。

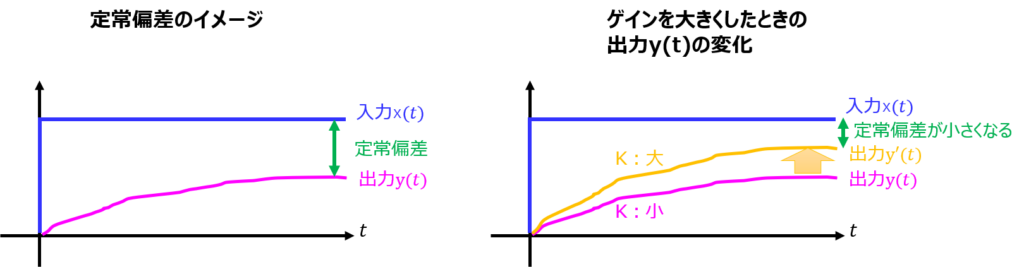
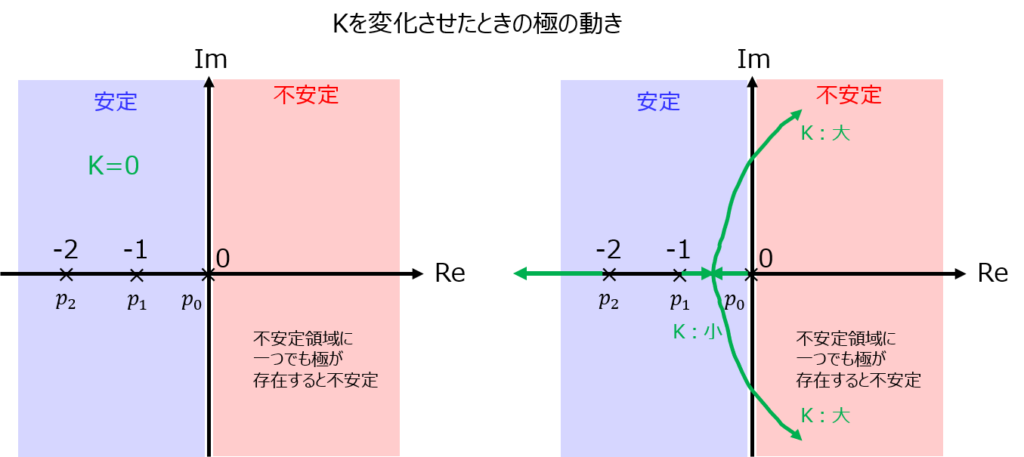
この式より、K=10,100の間で、極が正の領域に入ることが分かります。このとき、ラプラス逆変換するとexp(t)項が正になるので、t→∞を考えると発散します。

よって、Kを大きくすると、不安定になってしまうことが分かりました。このように、ゲインKを大きくしたときの極の動きを根軌跡と言います。(下図の緑色の線がそうです。)

また別記事で紹介しますが、安定性の評価に使用します。

定常偏差の求め方

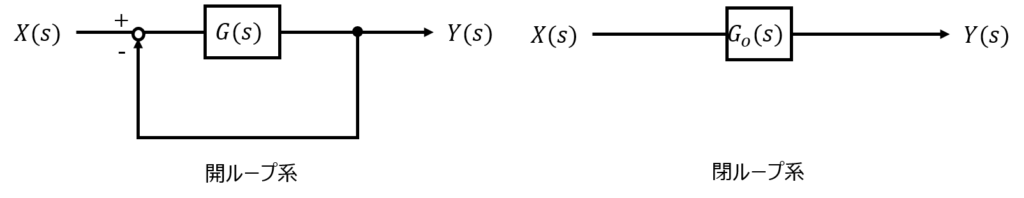
少し脱線しましたが、本題の偏差の求め方を説明します。

開ループ伝達関数を\(G(s)\)とすると、下記の式で表せます。

\begin{eqnarray}E(s)=\dfrac{1}{1+G(s)}X(s)\end{eqnarray}

これを最終値の定理を用いて定常状態の偏差を下記で求めることができます。

\begin{eqnarray}e(∞)=\lim _{s\rightarrow 0}sE\left( s\right) =\lim _{s\rightarrow 0}s\dfrac{1}{1+G\left( s\right) }X(s)\end{eqnarray}

定常状態ですので、極限で考える必要があります。

なお、最終値の定理を使わずとも、計算した出力Y(s)を逆ラプラス変換し、時間領域の出力\(y(t)\)を求める。⇒その極限(\(t→∞)\)を考えて、入力値と比較する方法もあります。

ただ、本問のように与えられた伝達関数が複雑な場合、手計算で逆ラプラス変換できないことが多いです。このため、s領域でそのまま定常偏差を求めることができる最終値の定理の使用をオススメします。

定常偏差を求めるうえでの注意点

(2)式をそのまま丸暗記することは危険です。

あくまでも、開ループ制御系の伝達関数\(G(s)\)に対し成立する式です。

閉ループ系では使用できません。

できれば、公式ではなく、入力に対する出力の差分という原則に基づいて問題ごとに式を導出した方が良いです。

下記では、開ループ系と閉ループ系での導出方法について説明します。

開ループ系での定常偏差

開ループ伝達関数、または閉ループ伝達関数で計算する過程が異なります。

\(E(s)=X(s)-Y(s)\)に対し

\(Y(s)=(X(s)-Y(s))G(s) ⇔ Y(s)=\dfrac{G(s)}{1+G(s)}X(s)\)を代入して

\begin{aligned}E(s)&=X(s)-\dfrac{G(s)}{1+G(s)}X(s) \\ &=\dfrac{1}{1+G(s)}X(s) \end{aligned}

となり、(2)式と一致しました。

閉ループ系での定常偏差

\(E(s)=X(s)-Y(s)\)から導出するところは同じです。

問題は、\(Y(s)=G_{o}(s)X(s)\)と、\(Y(s)\)と\(X(s)\)の関係式が開ループ系と異なります。

よって、

\begin{aligned}E(s)&=X(s)-G_{o}(s)X(s) \\ &=(1-G_{o}(s))X(s) \end{aligned}

となります。

実際は、\(G_{o}(s)=\dfrac{G(s)}{1+G(s)}\)ですので、これを代入すると(2)式と一致します。

与えられた伝達関数の”開”、”閉”をしっかり区別していれば問題ないのですが、与えられた伝達関数をただ公式に代入することの無いようご注意下さい。

解答

(5)定常偏差について

単位ステップ関数のラプラス変換は、\begin{eqnarray}X(s)=\dfrac{1}{s}\end{eqnarray}

\begin{aligned} E\left( s\right) &=X\left( s\right) -Y\left( s\right) \\ &=X\left( s\right) -\dfrac{KG}{1+KG}X\left( s\right) \\ &=\dfrac{1}{1+KG}X\left( s\right) \\ &= \dfrac{\left( s+1\right) ^{2}}{\left( s+1\right) ^{2}+Ke^{-Ls}\left( s+\sqrt{3}\right) }X(s)\end{aligned}

これより、最終値の定理から

\begin{aligned}\varepsilon &=\lim _{s\rightarrow 0}s\dfrac{\left( s+1\right) ^{2}}{\left( s+1\right) ^{2}+K\overline{e}^{Ls}\left( s+\sqrt{3}\right) }\cdot \dfrac{1}{s} \\ &=\dfrac{1}{1+\sqrt{3}K}\end{aligned}

(6)安定限界について

図(b)の伝達関数は\begin{eqnarray}G\left( s\right) =\dfrac{K\left( s+\sqrt{3}\right) }{\left( s+1\right) ^{2}}e^{-Ls}\end{eqnarray}

\begin{eqnarray}G\left( i\omega \right) =\dfrac{K\left( j\omega +\sqrt{3}\right) }{\left( 1+j\omega \right) ^{2}}\end{eqnarray}

\(\omega_{\pi}=\sqrt{3}\)のとき、\(|G(j \omega_{\pi})|=1\)なので

\begin{eqnarray}K \cdot \dfrac{\sqrt{6}}{4}=1 \\ K=\dfrac{4}{\sqrt{6}}\end{eqnarray}

\begin{aligned}\varepsilon =\dfrac{1}{1+\sqrt{3}\frac{4}{\sqrt{6}}}=\dfrac{1}{1+2\sqrt{2}}\end{aligned}

最後に

本問は、入力に対する定常偏差を説明しました。

外乱に対する定常偏差が問われるときもありますので、こちらは次回の記事で紹介します。