NANDのみ,NORのみを使用した論理回路の作成問題

問題

下記の論理関数を論理回路で表すことを考える。それぞれ2入力NANDのみ、NORのみを用いて示せ。

(1)\(f_{1}=xy+yz+xz\) (2入力NANDのみ)
(2)\(f_{2}=x+y\overline{z}\) (2入力NORのみ)

はじめに
解法の手順
解答例
最後に

はじめに

論理関数を論理回路で表す問題は、様々な大学の院試での頻出分野となります。

AND、OR、NOTなどの素子が与えられていれば、論理式をそのまま回路に落とし込むだけで良いですが、院試レベルとなるとそうもいきません。

NANDのみ、NORのみの使用で表記を求められることが多いです。

本記事では、解法の定石をまとめました。問題形式で学べますので、是非知識のチェックに役立てて下されば幸いです。

解法の手順

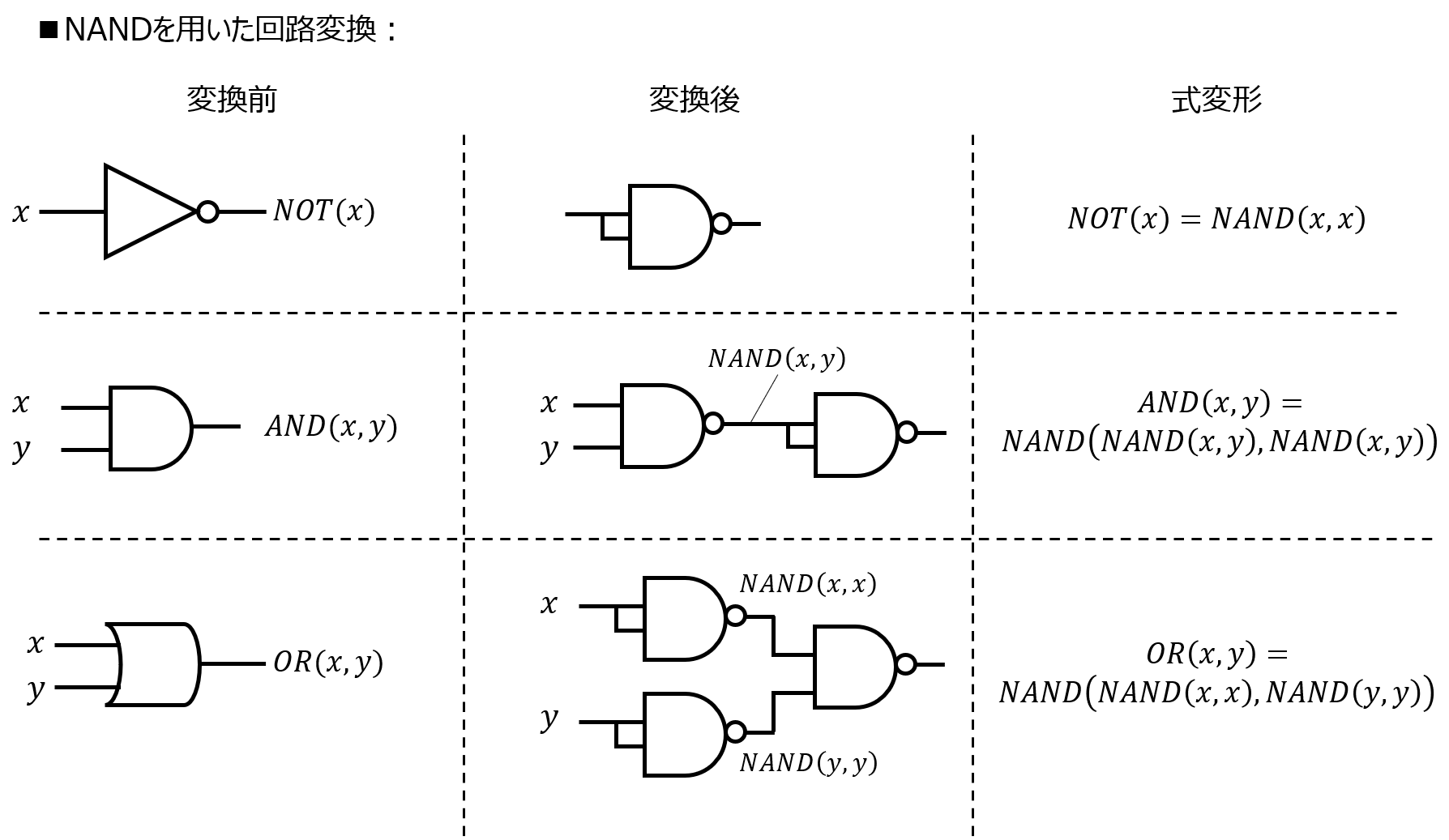
与えられた論理式を確認し、NAND\(\overline{xy}\)、NOR\(\overline{x+y}\)で表せない項を確認する。(AND、ORなど)
ドモルガン律を用いて、論理式をNAND/NORのみで表せる形に変形していく。
- NANDのみで表す場合：
  NOT→NAND：\(\overline{x}=\overline{xx}\)
  AND→NAND：\(xy=\overline{\overline{xy}･\overline{xy}}\)
  OR→NAND：\(x+y=\overline{\overline{xx}･\overline{yy}}\)
- NORのみで表す場合：
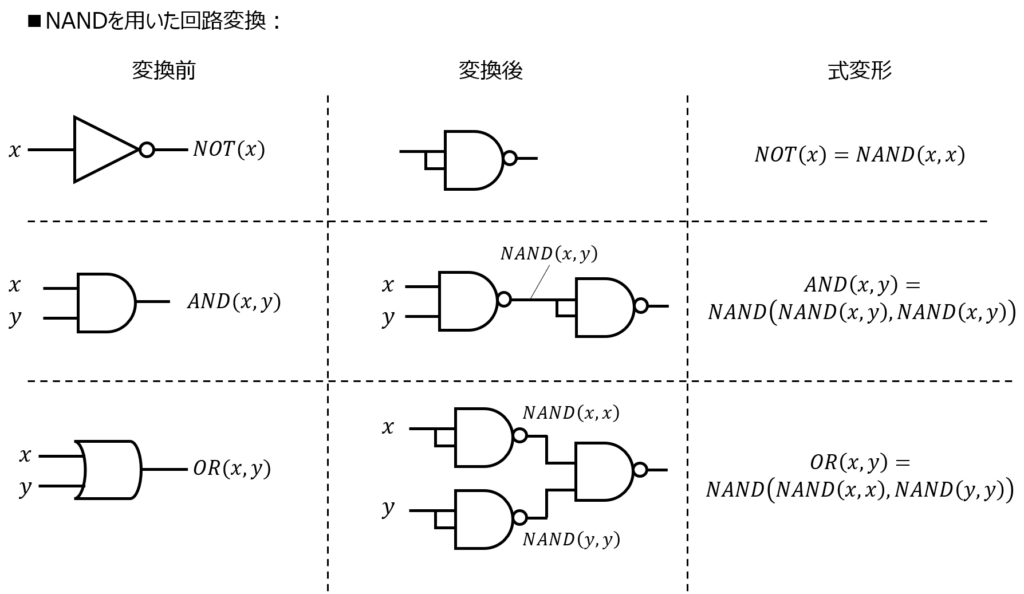
  NOT→NOR：\(\overline{x}=\overline{x+x}\)
  AND→NOR：\(xy=\overline{\overline{x+x}+\overline{y+y}}\)
  OR→NOR：\(\overline{\overline{x+y}+\overline{x+y}}\)

下記の図で表すことができます。

ドモルガン律の活用がキーになります。

以前の記事で説明したように、NAND/NORは完全系です。(任意の論理関数をNAND/NORのみで表すことができます)

NANDはそのままの形だとOR回路を持たないですが、ドモルガン律を用いることで、+演算子が出てきてORを表現できます。

NORは逆です。AND回路を持たないですが、同じくドモルガン律を用いることで、･AND演算子が出てきます。

このように、NAND/NORはNOT、AND、ORを持ちます。

なお、チェックボックスの変形には、べき等律\(x+x=x,x･x=x\)を用いています。

例えば、OR→NANDの変換の途中式は下記のようになります。

\begin{aligned}NOR(x,y)&=x+y\\ &=\overline{\overline{x+y}}\\ &=\overline{\overline{x}\cdot \overline{y}} \\ &=\overline{\overline{x･x}\cdot \overline{y･y}} \\ &=NAND(NAND(x,x),NAND(y,y)) \end{aligned}

この性質を用いて、与えられた問いを解答していきます。

解答例

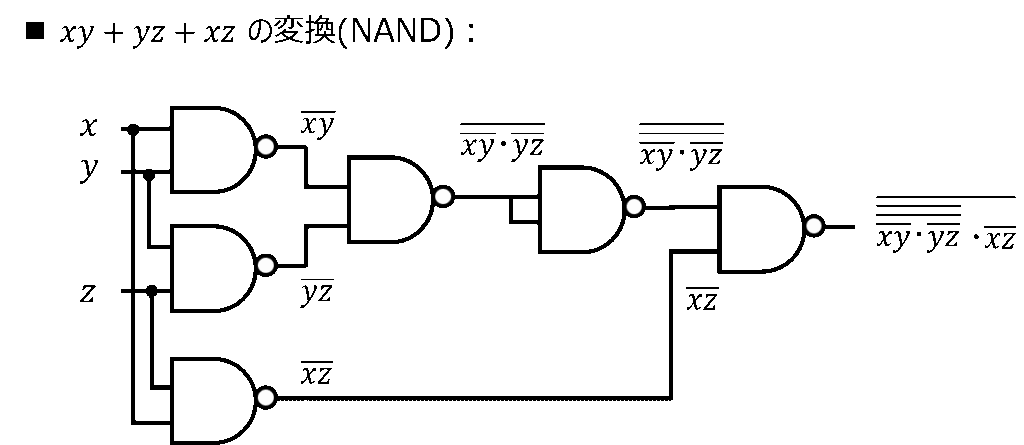
(1)\(f_{1}=xy+yz+xz\) (2入力NANDのみを用いて表せ。)

x=NOT(NOT(x))の関係を利用し、下記のように式変形する。

\begin{aligned}f_{1} &= xy+yz+xz \\ &= \overline{\overline{\overline{\overline{xy+yz+xz}}}} \\ &= \overline{\overline{\overline{\overline{xy}･\overline{yz}･\overline{xz}}}} \\ &=\overline{\overline{(\overline{\overline{xy}･\overline{yz}})+\overline{\overline{xz}}}} \\ &= \overline{(\overline{\overline{\overline{xy}･\overline{yz}}})･\overline{\overline{\overline{xz}}}}　\\&=\overline{(\overline{\overline{\overline{xy}･\overline{yz}}})･\overline{xz}} \end{aligned}

(2)式の最後より、2入力NANDを6個使用し、下記の論理回路を実装できる。

(2)\(f_{2}=x+y\overline{z}\) (2入力NORのみを用いて示せ。)

同じく、x=NOT(NOT(x))の関係を利用し、下記のように式変形する。

\begin{aligned}f_{2}&=x+y\overline{z} \\ &= \overline{\overline{x+y\overline{z}}} \\ &= \overline{\overline{x}･(\overline{y\overline{z}})} \\ &= \overline{\overline{x}･(\overline{\overline{\overline{y\overline{z}}}})} \\ &= \overline{\overline{x}･(\overline{\overline{\overline{y}+z}})} \\ &=x+(\overline{\overline{y}+z}) \\ &= \overline{\overline{x+(\overline{\overline{y}+z}) }} \\ &= \overline{\overline{x+(\overline{\overline{y+y}+z}) }}\end{aligned}

このように、NOR回路4つを用いて下記の論理回路を実装できる。