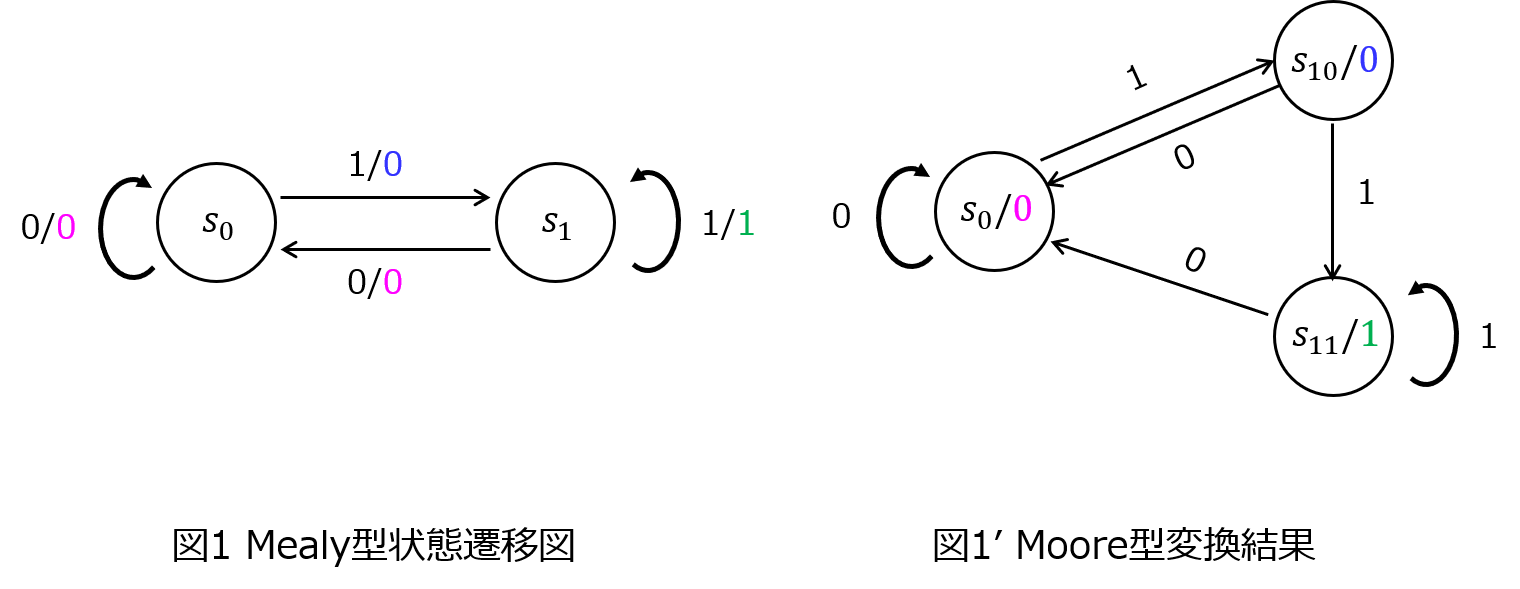(1)図1のミーリー型状態遷移図をムーア型状態遷移図に変換せよ。また両者の状態遷移表も作成せよ。
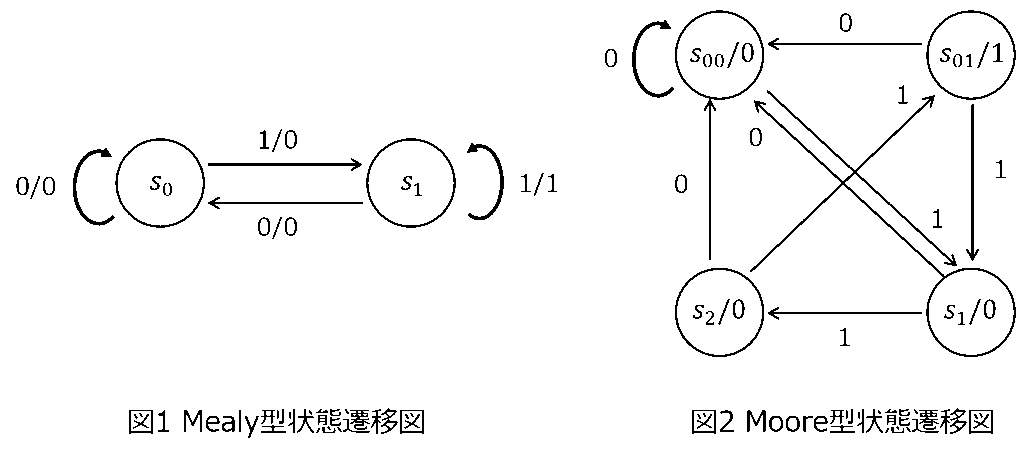
(2)図2のムーア型状態遷移図をミーリー型状態遷移図に変換せよ。また両者の状態遷移表も作成せよ。
順序回路における「状態」とは
システムの状態を示します。
例えば、入力系列”011″を検出し、最後の1を検出したときに出力1を返す順序回路を考えましょう。
011の順に入力されたことを判断しなければならないことから、少なくとも下記の4つの状態を区別する必要があると考えられます。
1.何も入力されていない状態
2.0が入力された状態
3.01が入力された状態
4.011が入力された状態
もし仮に、3.が無いと1が何回入ったか区別できず。1回目の1を検出したときに1を出力してしまうかもしれません。
同様に、2.が無いと11を検出してもその前に0が入っていたか分かりません。
このように、以前の入力とその結果を記憶したい場合、状態が必要です。
状態遷移図の種類
ある状態から別の状態への遷移条件を示した図を状態遷移図と言います。
状態遷移図には、Mealy(ミーリー)型、Moore(ムーア)型の2種類あります。

Mealy型状態遷移図
現在の状態と入力から出力が決定される状態遷移図です。
図1のように、状態を示す〇の中には、状態の数値。遷移条件の矢印に対し、入力/出力の順で記載します。
Moore型状態遷移図
現在の状態によってのみ出力が決まる状態遷移図です。
記載内容として、図2のように状態を示す〇の中に出力値も追加します。
遷移条件の矢印には、Mealy型と同じく入力値を記載します。
状態を表す〇の中に出力値も記載することから、同じ状態でも別の出力ならば〇を分けなければなりません。
状態数が増える欠点はありますが、出力回路が簡単になる利点があります。
Mealy型とMoore型の状態遷移の変換

- 状態遷移図の矢印に記載されている出力を遷移後の状態に移動
- 同一の状態があれば、既存の状態に合わせる
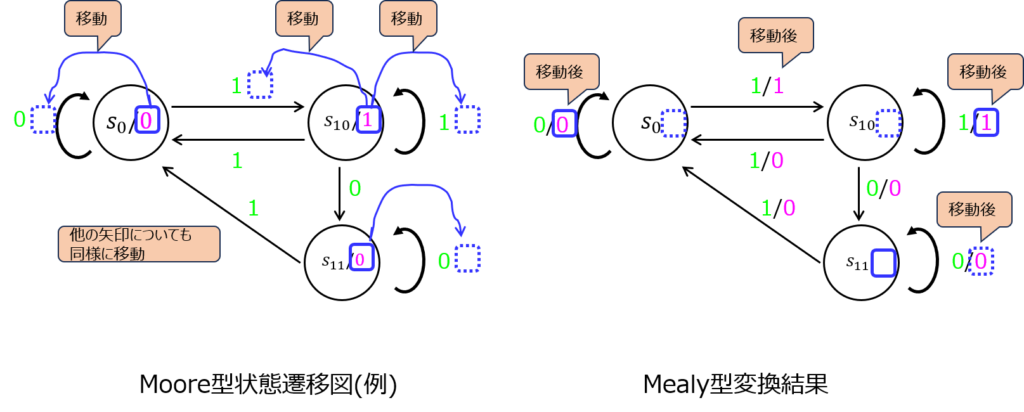
- 状態の〇の中に記載されている出力を、状態遷移条件の矢印の上に移動する
結局、出力値を遷移条件の矢印に移動するか、遷移先の状態に移動するかの違いです。
タイトルだけ見ると難しそうですが、実際の作業はシンプルです。是非覚えましょう。
注意:Mealy型順序回路では、等価な状態も別状態になっていることがあります。そのため、Mealy型からMoore型へ変換し、その後もう一度Mealy型に変換したときにもとに戻るわけではないです。
解答例
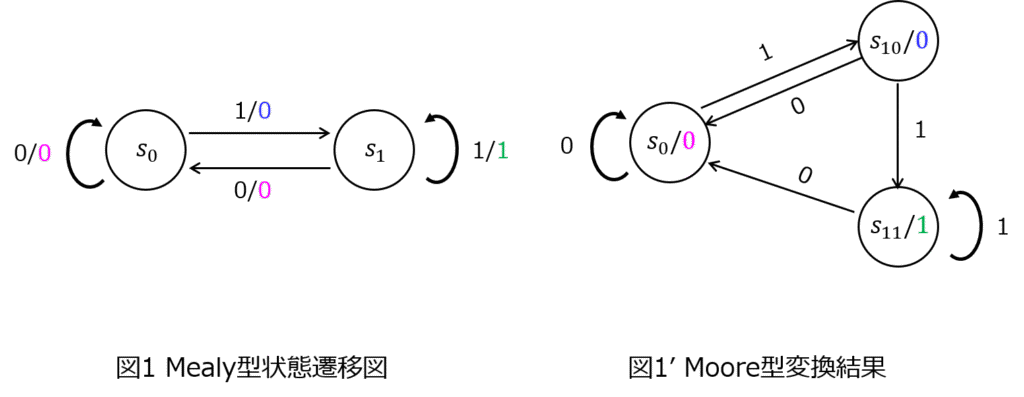
(1)状態遷移図の変換 Mealy→Moore
まず、それぞれの状態に遷移するときの出力を確認します。
\(S_{0}\)に遷移するときの出力:\(S_{0}→S_{0}:0,S_{1}→S_{0}:0\)
よって、\(S_{0}\)に遷移するとき、必ず0を出力することが分かります。
\(S_{1}\)に遷移するときの出力:\(S_{0}→S_{1}:0,S_{1}→S_{0}:1\)
よって、\(S_{1}\)に遷移するとき、0を出力するとき、1を出力するときの2通りあります。
以上より、\(S_{1}\)の状態は出力0,1で区別する必要があるため、下記になります。
(1)状態遷移表
(a)Mealy型状態遷移図は状態が2つ
(b)Moore型状態遷移図は状態が3つ
そのため、(a)の状態遷移表は2行。(b)の状態遷移表は3行あります。
| (a)Mealy型の遷移表 | 次状態 | 次状態 | 出力 | 出力 |
| 現状態 | 入力 0 | 入力 1 | 0 | 1 |
| \(S_{0}\) | \(S_{0}\) | \(S_{1}\) | 0 | 0 |
| \(S_{1}\) | \(S_{0}\) | \(S_{1}\) | 0 | 1 |
| (b)Moore型の遷移表 | ||
| 現状態 | 入力 0 | 入力 1 |
| \(S_{0}\) | \(S_{0}/0\) | \(S_{10}/0\) |
| \(S_{10}\) | \(S_{0}/0\) | \(S_{11}/1\) |
| \(S_{11}\) | \(S_{0}/0\) | \(S_{11}/1\) |
(2)状態遷移図の変換 Moore→Mealy
前章で述べたように、状態の中に入っている出力値を状態遷移の矢印に移動すれば良いです。
その結果、以下になります。
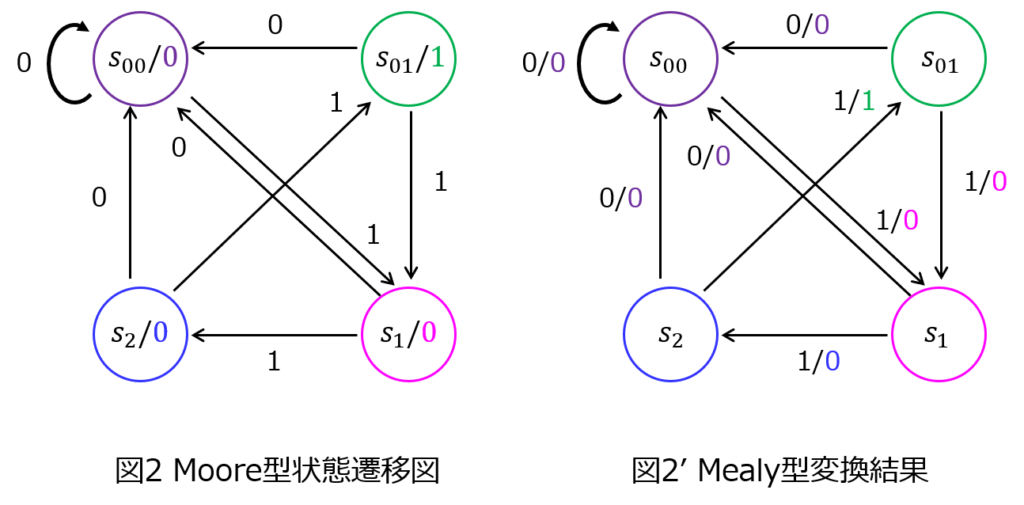
※問題集によっては、0を出力する状態\(S_{00}\)、1を出力する状態\(S_{01}\)をまとめて\(S_{0}\)とし、状態遷移の矢印に0を出力する場合、1を出力する場合を重複して記載しているものもあります。
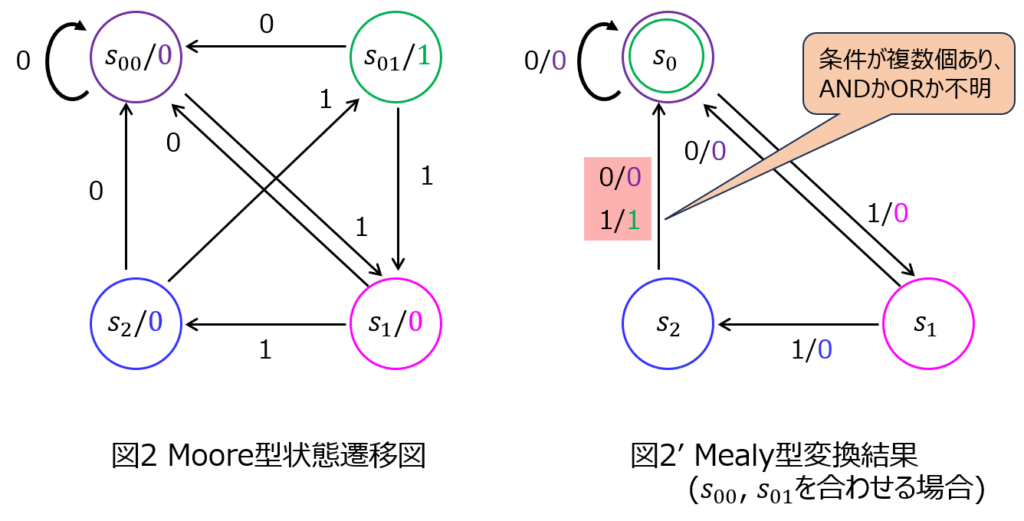
しかし、ソフトウェア設計を行う上で、遷移条件が2つあるものはorかandか区別する必要があります。
これを明確に記載しない上記の結果を答えとすることは、管理人としては避けた方が良いと思います。
そのため、最初に示したように、状態はまとめず遷移条件は別々に書くことを推奨します。
また、状態数が多くなると、遷移条件の矢印が抜けて全ての条件を網羅できないことがあります。
入力は0,1の2通りあることから、各状態から出ていく矢印も0,1の2通り存在するのか、確認することをオススメします。
(2)状態遷移表
Mealy型もMoore型も状態数は4つあるので、下記のようになります。
| (a)Mealy型の遷移表 | 次状態 | 次状態 | 出力 | 出力 |
| 現状態 | 入力 0 | 入力 1 | 0 | 1 |
| \(S_{0}\) | \(S_{0}\) | \(S_{1}\) | 0 | 0 |
| \(S_{1}\) | \(S_{0}\) | \(S_{1}\) | 0 | 0 |
| \(S_{2}\) | \(S_{0}\) | \(S_{0}\) | 0 | 1 |
| (b)Moore型の遷移表 | ||
| 現状態 | 入力 0 | 入力 1 |
| \(S_{00}\) | \(S_{00}/0\) | \(S_{1}/0\) |
| \(S_{01}\) | \(S_{00}/0\} | \(S_{1}/0\) |
| \(S_{1}\) | \(S_{00}/0\) | \(S_{2}/0\) |
| \(S_{2}\) | \(S_{00}/0\) | \(S_{01}/1\) |
最後に
Mealy型→Moore型への変換は、院試問題としてたまに見かけるものの、逆はあまり見ません。
まずは、前者をマスターすることをオススメします。