【順序回路】状態遷移表の簡単化(最小化)と例題

下記の状態遷移表にて、状態数の圧縮を行え。

状態遷移表	次の状態	次の状態	出力	出力
現状態	入力 $x=0$	入力 $x=1$	入力 $x=0$	入力 $x=1$
$S_0$	$S_2$	$S_3$	0	0
$S_1$	$S_1$	$S_1$	1	0
$S_2$	$S_1$	$S_6$	1	0
$S_3$	$S_4$	$S_5$	0	0
$S_4$	$S_1$	$S_0$	1	0
$S_5$	$S_2$	$S_3$	0	0
$S_6$	$S_4$	$S_5$	0	0

ディジタルコンピューティング 亀山充隆(著) 第6章 演習問題問1より

状態数の最小化を行う利点

プログラムが簡潔になり、分かりやすい。必要な素子数が少なくなり、開発コストを低減できる。など、良いことばかりです。

大学の講義だけでなく、実際のソフト開発現場でも、状態とそれぞれの意味する内容の検討は多々行います。

院試でもたまに出題される本分野ですが、実業務とも親和性が高いです。

感覚的にまとめてしまう人が(筆者含め)多いですが、本記事で正当な方法を理解できれば、業務の質も上がると思います。

なお、状態遷移の概要については、こちらの記事でまとめています。

状態数の最小化方法

平たく言えば、
１．入力に対する出力が他の状態と異なる状態は独立であること。
２．別の状態からある状態に遷移したとき、その状態も独立であること。

を厳密にチェックしていく方法になっています。

例えば、入力$x=0,1$に対する出力が$(0,1),(1,0)$になる状態が一つずつ存在したとします。

これをマージしてしまうと、出力がどちらに取れば良いか分からず、不定になってしまいます。
一方で、(0,1)を取る状態が複数個有るときは、まとめられる可能性が出てきます。

これをチェックすることが１．の過程ですね。

(0,1)を取る状態が複数個あった場合でも、遷移先が別の状態で異なる出力を出す場合、その状態をマージしてしまうと影響先が発生してしまう。

このため、遷移先含めてマージできるのか確認することが２．の過程を表しています。

実際に、問題を解いて確認していきます。

なお、問題内容自体は教科書から引用しましたが、略解しか無かったので、導出過程は全て管理人で作成しました。

解答例

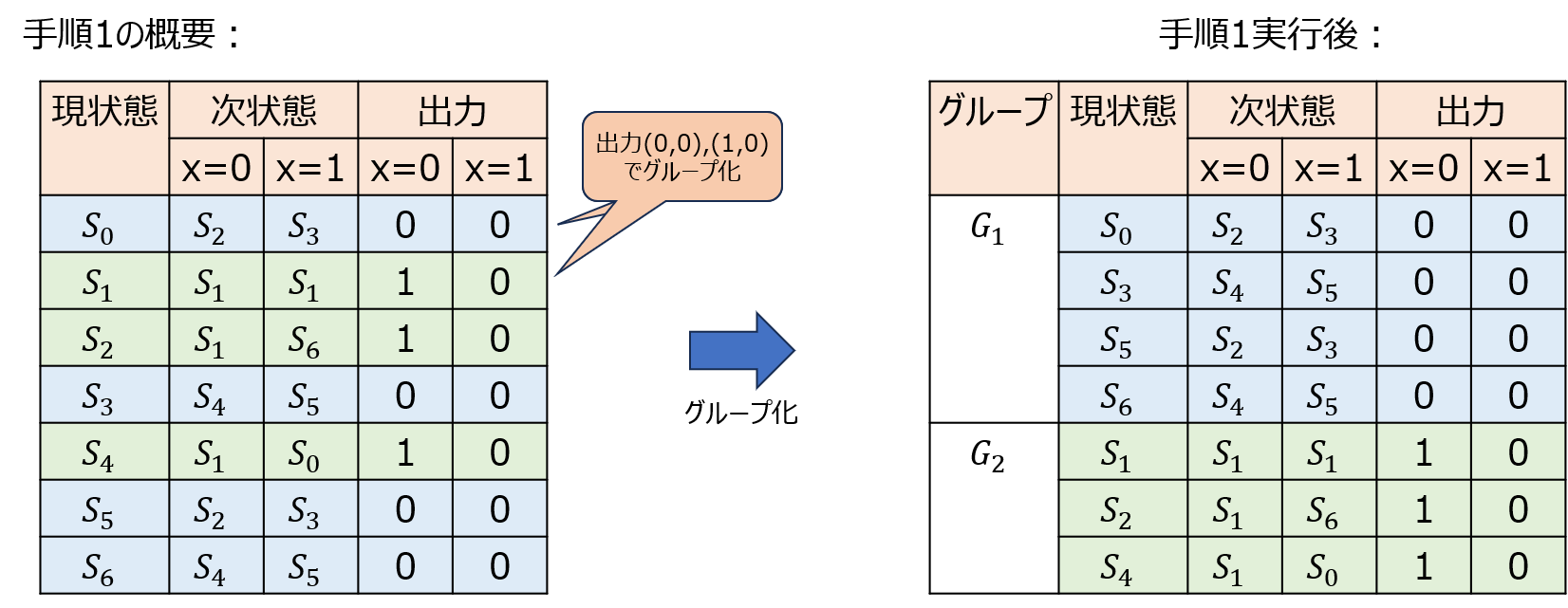
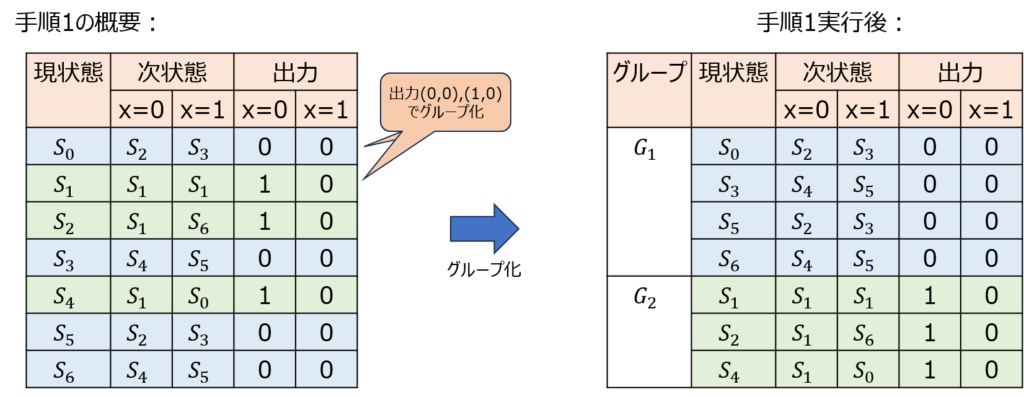
手順1 出力が同じ状態のグループ分け

与えられた状態遷移表より、下記の2グループに分けられる。

グループ$G_1$：$S_0,S_3,S_5,S_6$
グループ$G_2$：$S_1,S_4,S_5$

手順2、３ 遷移先のグループの確認。分割

グループ$G_1∊(S_0,S_3,S_5,S_6)$について：

いずれの状態も$x=0$でグループ$G_2$、$x=1$でグループ$G_1$に遷移する。

よって、全て同じ状態にまとめられる。

グループ$G_2∊(S_1,S_2,S_4)$について：

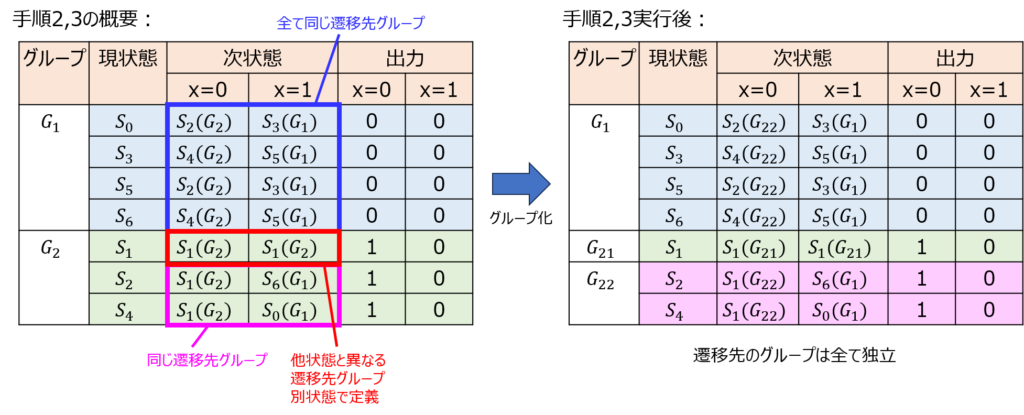
$x=0$でグループ$G_2$に遷移は同じだが、$S_1$のみ、$x=1$でグループ$G_2$に遷移する。

よって、$S_1$のみ同じ状態にできないため、状態をさらに分割する。

$G_{21}∊S_1$、$G_{22}∊(S_2,S_4)$とすると、遷移先が全て同じのグループになる。

また、グループ$G_1$の$x=0$遷移先は全て$G_{22}$

以上より、下記の3状態にまとめることができる。

状態1：$S_0,S_3,S_5,S_6$
状態2：$S_1$
状態3：$S_2,S_4$

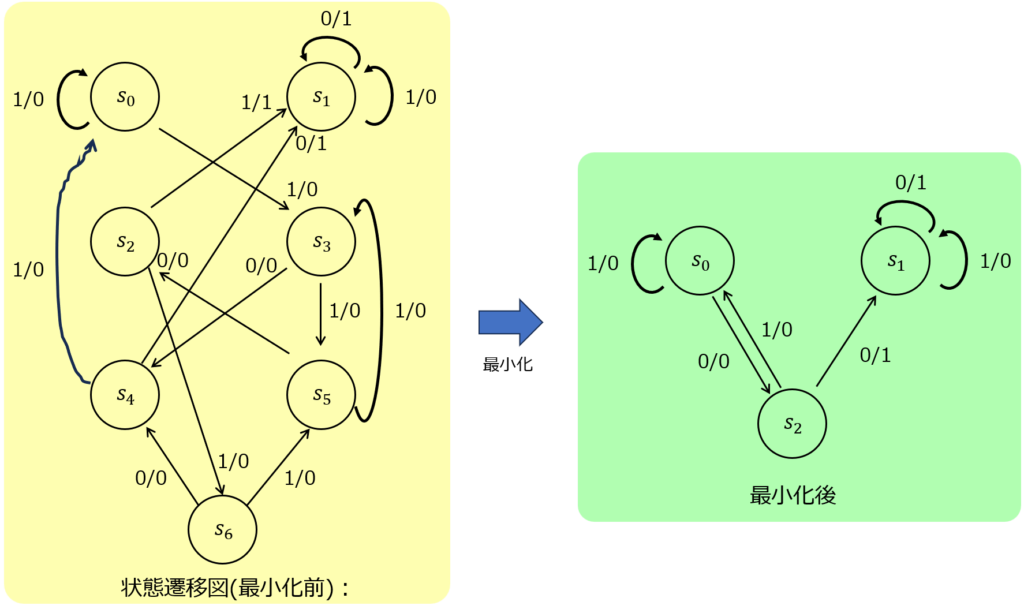
補足：状態遷移図について

下記のようにまとめられます。

複雑だったものが3つにまとまり、分かりやすさが一目瞭然です。