(1)下記の言語が正規言語ではないことを反復補題を利用して証明せよ。
\begin{eqnarray}L=({a^{n},b^{n} | n≧0})\end{eqnarray}
(2)自由文脈文法\(G_{1}=(N_{1},\Sigma_{1},P_{1},S_{1})\)の生成規則の集合\(P_{1}\)を与えよ。ただし、\(N_{1}=S_{1},\Sigma_{1}=(a,b),S_{1}\)はそれぞれ非終端記号の集合、終端記号の集合、開始記号とする。
はじめに
オートマトンを試験範囲とする大学で、たまに出題される証明問題です。ネットで検索すると、講義資料では説明されていますが、文章として説明する場所が無いように見えました。ですので、今回紹介します。
※頻出問題としては、ある言語Lが与えられ、それに対応するオートマトンを作成する問題があります。こちらに関しては別サイトでの解説が豊富なので、今回は省略します。
標記の問題、皆様はどのような証明を考えますでしょうか。
直感的な証明方法
私が一番最初に考える証明方法は下記です。
\(a^{n},b^{n}\)であるため、aが出た回数分bが発生する必要がある。しかし、nに上限値が無いため、aが出た回数を記憶するために必要な状態が限りなく必要。
状態を規定できないため、正規言語ではない。
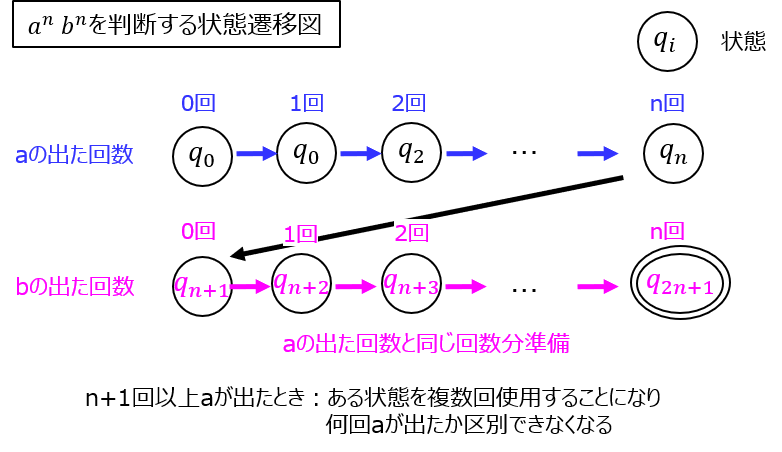
こちらの証明方法、ネットでもよく説明されていると思います。実際、試験という限りのある時間であれば、こちらで満点近く得点できるのではないかと考えています。
ただ、少し直感的な説明であることが否めません。数式を用いて、厳密的な証明ができないのでしょうか。
そういった時に出てくる方法が、今回紹介する「反復補題」です。上記の証明方法を背理法として説明しているに過ぎないのですが、実際に厳密的な証明を求められたときに役立つ考え方と思います。
反復補題を使用した証明方法
反復補題とは
与えられた言語Lが正規言語ならば、Lの長さがm以上の任意の系列wが存在します。
また、w=xyzと適当な文字列xyzに分割することができ、以下の条件を満たすことを言います。
- 任意の整数i≧0に対し、\(xy^{i}z∊L\)
- \(|y|≧1\)
- \(|xy|≦m\)
w=xyzの文字列のうち、xとzの間にあるyの個数を変化させても、その結果発生した文字列は変わらずLに属することを指しています。
今回は、背理法を用いて上記と矛盾することを証明します。
これにより、言語\(L\)は正規言語ではないことが分かります。しかし、文脈自由言語ではあります。ですので、ある生成規則\(P_{1}\)に基づいて表現できるものになります。(2)で詳しい説明をしますが、生成規則を与えるには、\(n=0,1,2…\)と数を上げていき(実験)、共通の生成ルールを見つけていくことが解答の定石になります。
解答例 (1)
\( L=({a^{n},b^{n} | n≧0}) \) が正規言語とすると、ある自然数mを使用して文字列\(w=a^{m}b^{m}\)が存在する。
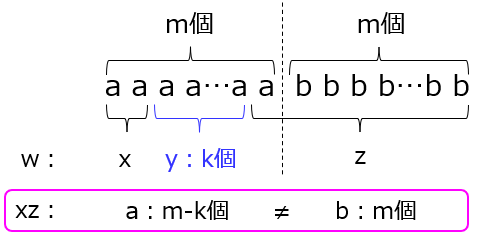
w=xyzとする。反復補題の条件2により、yは空集合ではない。反復補題の条件3により、|xy|≦mである。
このとき、yは文字aのみを含む。yに属する文字aの個数をk個(1≦k≦m)とすると、xzはaをm-k個、bをm個含み、個数は一致しない。
このとき、反復補題の条件1 \(xy^{i}z∊L\)が成立するか確認する。i=0とすると、\(xz=xy^{i=0}z\)で、仮定よりLに属するはず。
しかし、前述の通りxzにあるaとbの個数は一致しないため、仮定に矛盾する。
反復補題1に反するため、xzはLに含まれない。
解答例 (2)
まず、\(n≧0\)より、空集合\(∅\)が考えられます。
\(n=1\)のとき、\(ab\)、\(n=2\)のとき、\(aabb\)、\(n=3\)のとき、\(aaabbb\)だから
\(aS_{1}b\)の生成規則を用いれば、任意の\(n\)に対して言語\(L\)を表現できる。
以上より、求める生成規則は、\(P_{1}=(aS_{1}b | ∅)\)
最後に
オートマトンの問題は、文字列の規則性、状態遷移図の概要を手書きで実験して、その後与えられた問に答えることが多いです。
正規言語でないことの厳密な証明は、本問の考え方をベースに行います。
他、正規言語でない文字列は他にもあるため、十分に演習を積むことをオススメします。
参考文献
計算理論とオートマトン言語理論:丸岡 章 (著) P79,80