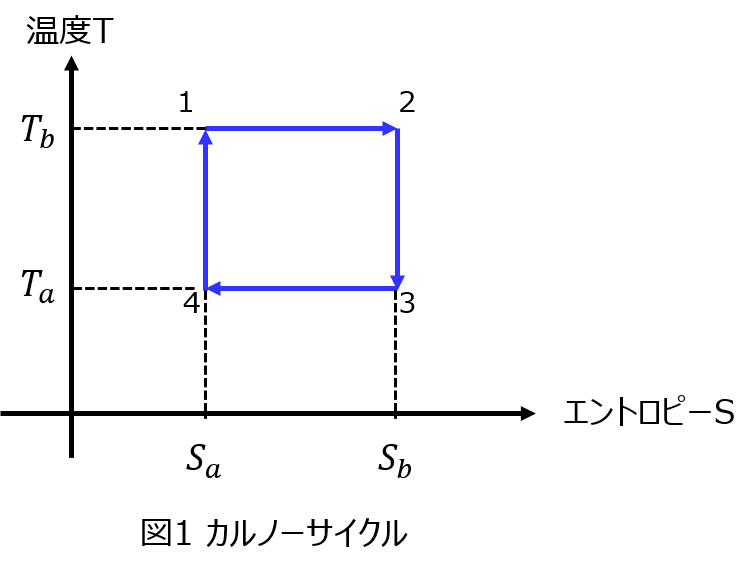
図1は、火力発電の基礎となるカルノーサイクルT(温度)-S(エントロピー)線図である。1molの理想気体が、図に示す1,2,3,4,1の順に状態(S,T)を変える時の、各変化過程をA,B,C,Dとする。この理想気体の定積比熱を\(C_{v}\)として、以下の問いに\(T_{a},T_{b},S_{a},S_{b},C_{v}\)のみを用いて答えなさい。
(1)過程Aと過程Cは等温変化で、過程Bと過程Dは断熱変化である。それぞれの過程で、気体が外部にした仕事を求めなさい。
(2)過程Aで気体が熱源から得た熱量Qを求めなさい。
(3)1サイクル全体で期待が外部にした仕事の総和をWとして、(b)の熱量Qに対するWの比\(\frac{W}{Q}\)を求めなさい。
神戸大学大学院 電気電子工学専攻 電力工学 2022より抜粋
T-S線図とは
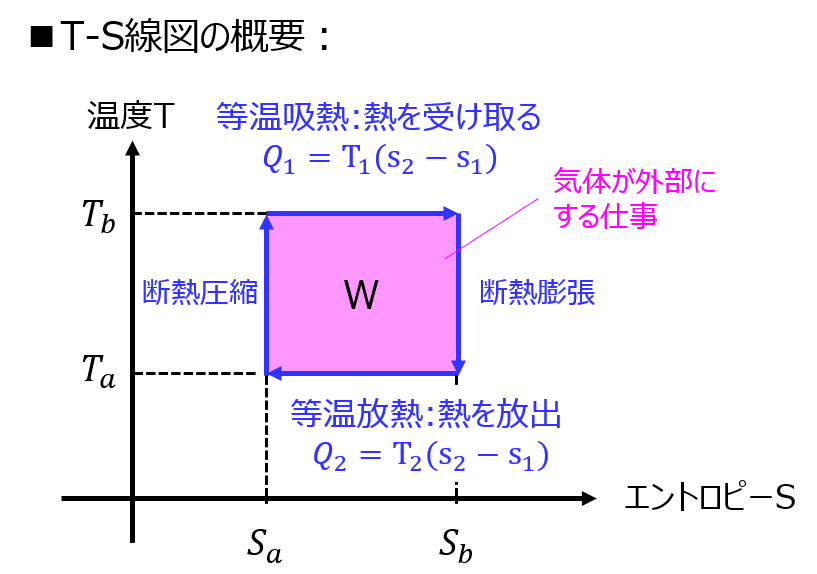
温度(縦軸)とエントロピー(横軸)の関係を表した図を言います。
エントロピーは、粒子の乱雑さを言います。
エントロピーが変化せず、温度が上昇(下降)する過程を断熱圧縮(膨張)と言います。
一方で、温度が変化せず、エントロピーが上昇(下降)する過程を等温吸熱(放熱)と言います。
この過程を繰り返すことで、T-S線図に閉路が出来ます。
閉路分の面積が、対象の熱機関が外部にもたらす仕事になっています。
カルノーサイクルとは
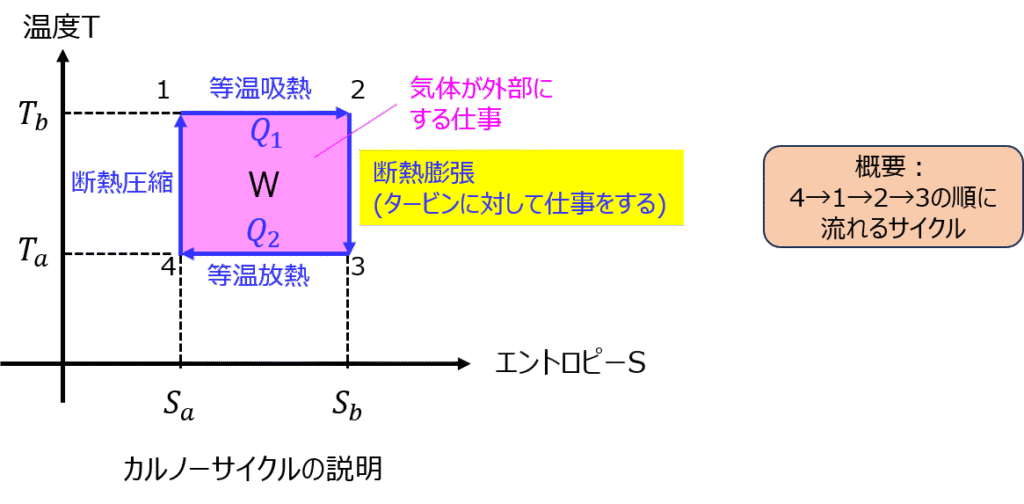
等温膨張、断熱膨張、等温圧縮、断熱圧縮の順に行われるサイクルを言います。
“断熱”が付く変化は、エントロピーがそのままで、温度のみが変化します。外部から熱を吸収/放出しません。気体内部の系で仕事をしたことを意味しており、この時にタービンを回しています。
これは、エントロピー変化\(dS=\frac{dQ}{T}\)であることが関係しています。外部から熱を受けないので\(dQ=0\)。右辺が0になるので、\(dS=0\)になるわけですね。
“等温”が付く変化は、温度がそのままで、エントロピーが変化します。気体の系に熱が加わった。または出ていったことを意味しています。
ランキンサイクルとは
カルノーサイクルは、火力発電によらず、熱力学を勉強する上で基礎的な考え方になります。
一方で、火力発電を考える際、現場に即したより現実的なサイクル(T–S線図)を考える必要があります。
ここで使われる考え方が、ランキンサイクルです。(下図)
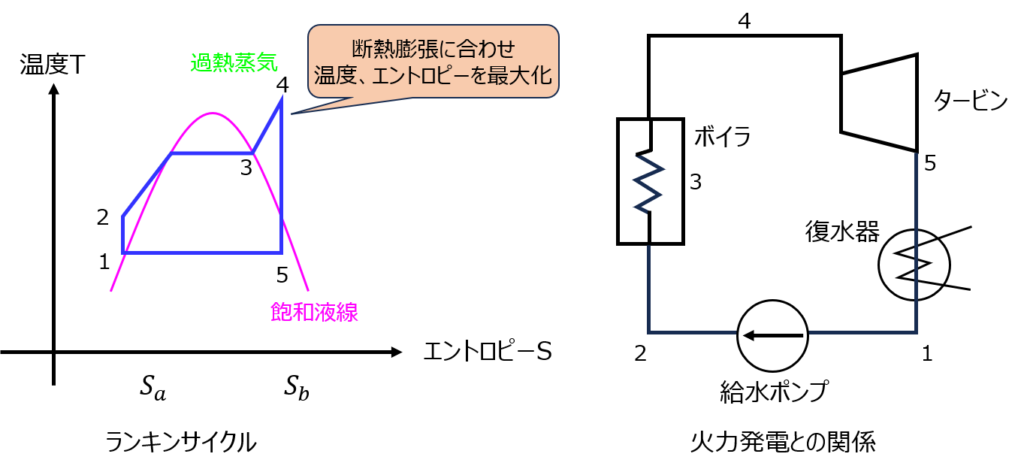
飽和液線に沿って気体の系が変化していきます。線より上部の領域が蒸気になっています。
特に、タービンで仕事をするときは高い温度、エントロピーから断熱膨張し、仕事をします。(過熱蒸気)
補足:熱効率を大きくしたときの課題 (タービンの腐食)
熱効率を高めたいとき、なるべく断熱膨張する量を大きくする。
➡T-S線図の温度を下げて面積を最大化する。と考えたくなります。
具体的な方策としては、高圧タービンの他、中圧タービン、低圧タービンなど、複数個のタービンを繋ぐことが挙げられます。
ただし、温度を低くし過ぎると、新たに発生する課題もあります。蒸気が水となり、高速で回っているタービンの羽根に当たることで穴が開いてしまいます。これにより、メンテ費用が高くなるデメリットがあります。
そのため、最大化可能な熱効率には限りがあります。
解答例
(a)気体の仕事
熱力学の第一法則:\(dQ=dU+dW\)を用いて考える。
ただし、\(dQ\)は気体の得る熱量。\(dU\)は気体の温度変化。\(dW\)は気体が外部に行う仕事とする。
過程A:\(dU=0\)より、\(W_{A}=T_{b}(S_{b}-S_{a})\)
過程B:\(dQ=0\)より、\(W_{B}=C_{v}(T_{b}-T_{a})\)
過程C:\(dU=0\)より、\(W_{C}=T_{b}(S_{a}-S_{b})\)
過程D:\(dQ=0\)より、\(W_{D}=C_{v}(T_{a}-T_{b})\)
(b)気体が外部から得た熱量 (過程A)
(a)の結果を引用し、\begin{aligned}Q=T_{b}(S_{b}-S_{a})\end{aligned}
(c)仕事の総和と熱量の比
仕事の総和は、閉路ABCDの面積に等しいので
\begin{aligned}W=(T_{b}-T_{a})(S_{b}-S_{a})\end{aligned}
これと、(b)の結果を引用し
\begin{aligned}\dfrac{W}{Q}&=\dfrac{(T_{b}-T_{a})(S_{b}-S_{a})}{T_{b}(S_{b}-S_{a})} \\ &=1-\dfrac{T_{a}}{T_{b}}\end{aligned}
最後に
本問は、電験3種の電力分野でも出題されることがあります。
T-S線図の面積が、外部に対して行った仕事である。という考え方は必ず覚えておきましょう。