風力発電に関する以下の文章について、(A)~(D)に入れるべき数値または式をそれぞれ答えなさい。
風のもつエネルギーは、風速を\(v\)、空気の密度を\(\rho\)、考える断面積を\(A\)とすると、単位時間あたり(A)と表される。例として、\(\rho=1.2kg/m^{3}\)、ロータの半径が\(10m\)、\(v=10m/s\)の場合、風車の受ける単位時間あたりのエネルギーは、(B)kWとなる。
神戸大学大学院 電気電子工学専攻 電力工学 2019より抜粋
ロータによって\(v_{1}\)の風速が\(v_{2}\)に低下する割合を\(\xi=(v_{1}-v_{2})/v_{1}\)で定義する。風車のロータ効率は、\(\eta=4\xi(1-\xi)^{2}\)と計算される。この効率は\(\xi=(c)\)のときに最大値\(\eta_{max}=(D)\)となる。
風力発電とは
風の力で風車を回し、回転エネルギーを電気エネルギーに変換する発電方式です。
地方をドライブするときによく見かけるかもしれません。風を受けやすい平原、山の頂上などでよく配用いられます。
風力発電機の構成
3枚翼プロペラ形風車がよく用いられます。
これは、3つの翼を主軸に取り付け、ナセルを接続し、基礎までタワーを立てる方式です。
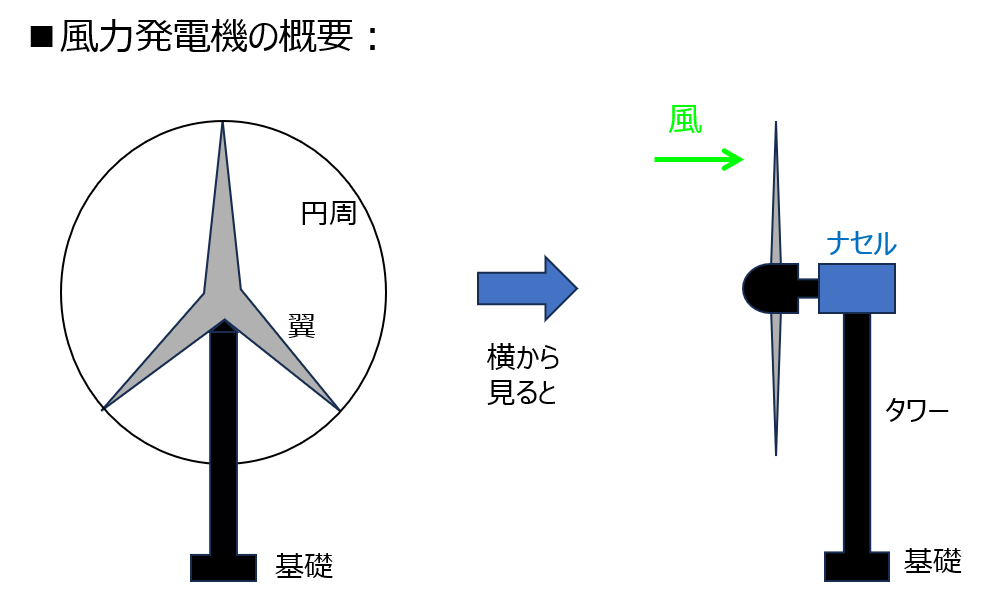
ナセルには、増速器、発電機などが内蔵されており、風で翼が回り始めた時、回転数を底上げ、電気エネルギーに変換します。
発電機は、誘導発電機が良く用いられており、交流で発電します。
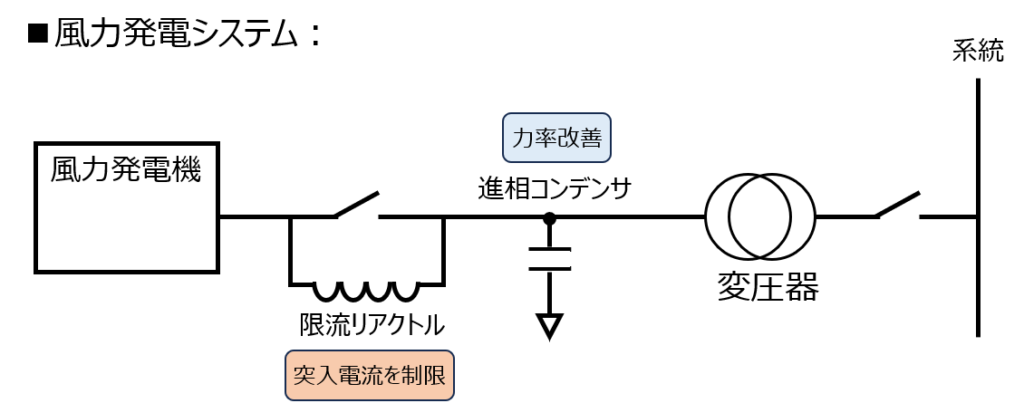
そのため、変圧器を間に挟むことで系統と接続することができます。なお、系統に接続する際は突入電流が流れるため、限流リアクトルで電流量を調整します。
他、力率改善のために進相コンデンサも接続します。自己励磁防止のため、誘導発電機のインダクタンスと共振を起こさない範囲でキャパシタンスを調整する必要があります。
発電電力(理論値)
運動エネルギー\(E=\frac{1}{2}mv^{2}\)の考えをベースにします。
水力発電と同様、風車の場合も質量\(m\)は\(m=\rho A v{2}\)と表すことができます。
速度が大きいほど、単位時間当たりのある領域を通過する風の体積が大きいため、質量\(m\)が大きくなる考え方です。
よって、運動エネルギーは
\begin{aligned}E=\dfrac{1}{2}\rho A v^{3}\end{aligned}
と速度の3乗で表すことができます。この考え方は電験でもよく出てきます。
ロータ効率の導出
問題文では端折って、結果\(\eta=4\xi(1-\xi)^{2}\)だけ記載していますが、本節では簡易的に導出をします。
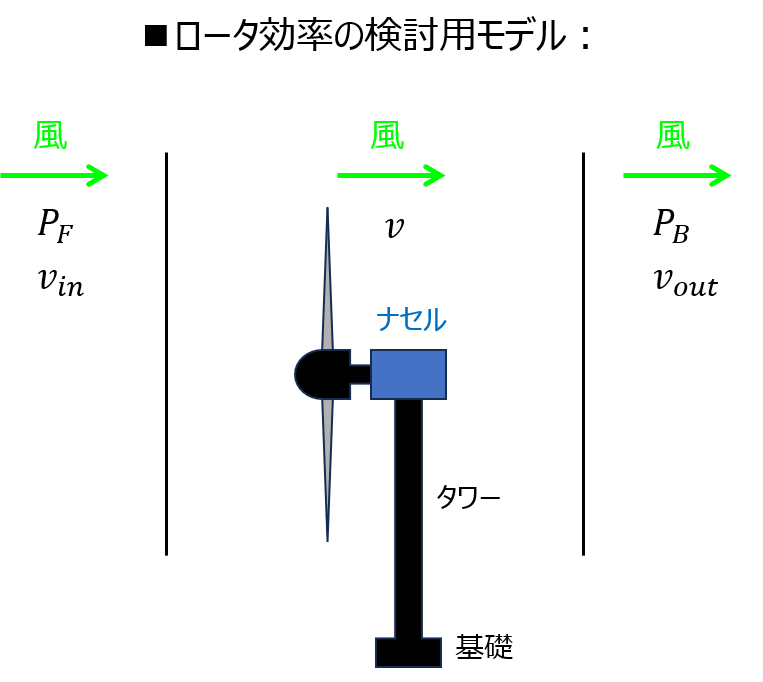
ローター入口の圧力を\(P_{F}\)、速度を\(v_{in}\)、ローターの出口部分の圧力を\(P_{B}\)、速度を\(v_{out}\)とする。また、ローター部分の速度を\(v\)、大気圧を\(P_{a}\)とする。
ローター内では、速度が線形的に減少すると仮定する。このとき\(v\)と速度減少率\(\xi\)は
\begin{cases}v=\dfrac{v_{in}+v_{out}}{2} \\ \xi=\dfrac{v_{in}-v}{v_{in}}\end{cases}
と表すことができる。(ロータは入り口と出口の中間にあると仮定)
また、ベルヌーイの定理より
\begin{cases}\dfrac{1}{2}\rho v_{in}^{2}+P_{a}=\dfrac{1}{2}\rho v^{2}+P_{F} \\ \dfrac{1}{2}\rho v^{2}+P_{B}=\dfrac{1}{2}\rho v_{out}^{2}+P_{a}\end{cases}
で、これを簡単化すると
\begin{aligned}P_{F}-P_{B}=\dfrac{1}{2}\rho(v_{in}^{2}-v_{out}^{2})\end{aligned}
風がロータにおよぼす力\(F\)は圧力変化分を考えれば良く
\begin{aligned}F=(P_{F}-P_{B})A\end{aligned}
流体がロータに与える単位時間あたりの仕事\(P\)は、(4)(5)式を利用すれば良く
\begin{aligned}P&=Fv \\ &=\dfrac{1}{2}\rho(v_{in}^{2}-v_{out}^{2})Av \end{aligned}
最後に(2)式を\(v,v_{out}\)について代入することで
\begin{aligned}P=\dfrac{1}{2}\rho A v_{in}^{3}・4\xi(1-\xi)^{2}\end{aligned}
を得る。
効率\(\eta\)は、(7)式に流体の入力パワー\(\dfrac{1}{2}\rho A v_{in}^{3}\)を除算すれば良く
\begin{aligned}\eta=4\xi(1-\xi)^{2}\end{aligned}
以上が導出過程である。
補足 風速が大きくなった時の回転数制御
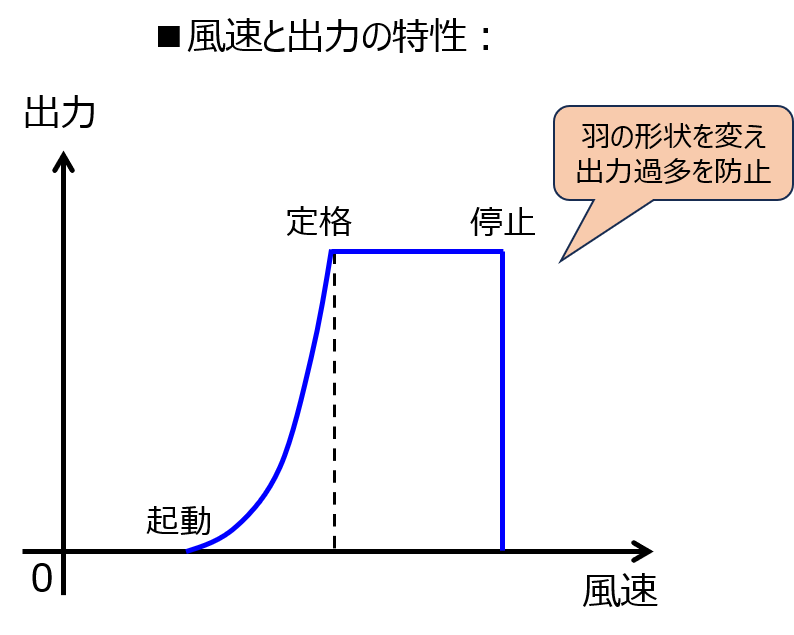
各発電器には定格出力が定められており、それに対応する風速も想定されています。
風速が定格出力以下の場合は、(1)式より風速の3乗に比例しますが、定格出力より大きくなった時はどうなるでしょうか。
この時は、翼の受け手面を風速のベクトルと平行にし、出力を落とす制御を実施します。(ピッチ制御)
こうすることで、システムの故障を防止できます。
解答例
(A)(B)単位時間あたりのエネルギーの計算
(A):前節の説明より、(1)式で表される。
(B):(1)式に与えられたパラメータを代入することで
\begin{aligned}E&=\dfrac{1}{2}*1.2*10^{2}*\pi*10^{3} \\ &=60\pi [kW]\end{aligned}
(C)(D)ロータ効率の最大値の計算
\(\eta=4\xi(1-\xi)^{2}\)を\(\xi\)で微分すると
\begin{aligned}\eta’&=4(1-\xi)^{2}+4\xi*2(1-\xi)*(-1) \\ &=12\xi^{2}-16\xi+4\end{aligned}
()式=0を考えると、\(\xi=\frac{1}{3},1\)
このとき、増減表は下記になる。
| \(\xi\) | 0 | ・・・ | 1/3 | ・・・ | 1 |
| \(\eta’\) | – | + | 0 | – | – |
| \(\eta\) | – | ↑ | 最大値 | ↓ | – |
増減表より、\(\eta=\frac{1}{3}\)のとき、最大値
\begin{aligned}\eta_{max}=4*\dfrac{1}{3} \left(1-\dfrac{1}{3} \right)^{2}\end{aligned}
を取る。
参考文献
電気エネルギー工学 八坂 保能(編著) P84~87


