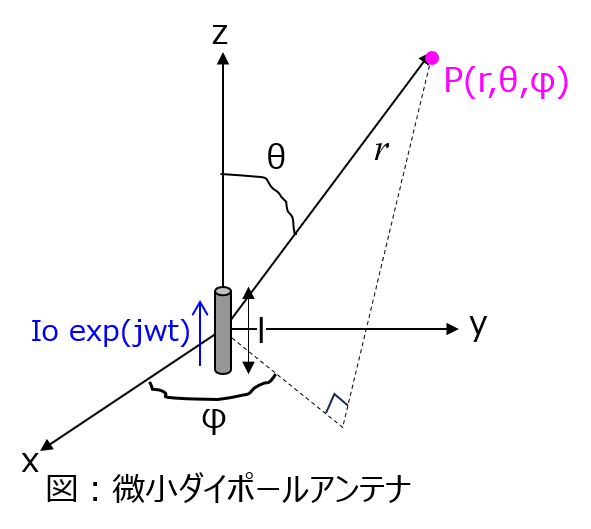
下記のように、長さ\(l\)の波長\(\lambda\)より十分短い微小ダイポールアンテナを考える。\(z\)方向に対し、電流\(I_{o}\exp(j \omega t)\)が流れているとして、下記の問いに答えよ。
(1)点P(r,θ,φ)におけるベクトルポテンシャル\(\boldsymbol{A}\)と電場\(\boldsymbol{E}\)、磁場\(\boldsymbol{H}\)を答えよ。なお、点Pは、アンテナに対し十分遠方に存在するとする。
(2)距離が十分に長いと無視できる成分を考慮し、(1)で求めた電場、磁場の放射界をそれぞれ答えよ。
ダイポールアンテナとは
直線状の導体から構成され、交流電流を流して周囲に電磁波を発生させる電気機器になります。問題で与えた図が特に分かりやすいです。
電磁波を生成すると、遠方にある物質に対し誘導電流を発生させ、電力、情報のやり取りをすることができます。この操作に対し、ダイポールアンテナでは以下の利点があります。
- シンプルな構造で製作が容易
- 全方向の指向性を持ち、任意の点で電磁波を受信できる
この利点から、ラジオのアンテナ、無線機でよく使用されています。
本記事では、実際に問題を解いてみることで、遠方の点に対し電磁波が及ぼす作用を見ていきます。
解答例
ベクトルポテンシャルを求め、その回転を取って磁場を算出します。
全体方針
まず、直交座標のベクトルポテンシャル\(A_{x},A_{y},A_{z}\)を考えて、そこから極座標\(A_{r},A_{\theta},A_{\phi}\)に変換することを考えます。
\begin{cases}A_{r}=A_{z}\cos\theta \\ A_{\theta}=-A_{z}\sin \theta \\ A_{\phi}=0 \end{cases}
の関係で変換することができます。
そこから、ベクトルポテンシャルと磁場の式
\begin{aligned}\boldsymbol{H}=\dfrac{1}{\mu_{o}}\Delta×\boldsymbol{A}\end{aligned}
及び、マクスウェル方程式(電磁誘導の法則)から
\begin{aligned}\Delta × \boldsymbol{H}=j \omega \varepsilon_{o}\boldsymbol{E}\end{aligned}
の関係を用いて各々の具体的な式を算出。r→∞の近似を考えて放射界を考えます。
ベクトルポテンシャルについて
電流ベクトルはz方向のみ向いているため
\begin{cases}A_{x}=0 \\ A_{y}=0\end{cases}
z成分については、ベクトルポテンシャルの式を使えば良い。
\begin{aligned}A=\dfrac{\mu_{o}Idl}{4 \pi r}\end{aligned}
について、\(r\)は\(l\)に対して十分に大きいので、一定値を乗算すれば良く
\begin{aligned}A_{z}=\dfrac{\mu_{o}I_{o}l}{4 \pi r} e^{-jkr}\end{aligned}
(2)式より、磁場\(\boldsymbol{H}\)を求める。
\begin{aligned}\nabla \times A=\begin{vmatrix}
\dfrac{\widehat{r}}{r^{2}\sin \theta } & \dfrac{a}{r\sin \theta }\widehat{\theta} & \dfrac{\phi }{r}\widehat{\phi} \\
\dfrac{\partial }{\partial r} & \dfrac{\partial }{\partial \theta } & \dfrac{\partial }{d\phi } \\ A_{r} & A_{\theta} & A_{\phi} \end{vmatrix}\end{aligned}
で、\(A_{\phi}=0\)なので
\begin{cases}H_{r}=0 \\ H_{\theta}=0 \\ H_{\phi}=\dfrac{I_{o}l}{4 \pi}\left(j\dfrac{k}{r}+\dfrac{1} {r^{2}}\right) \sin \theta e^{-jkr}\end{cases}
電場については、(3)式により
\begin{cases}E_{r}=\dfrac{IlZ_{o}}{2 \pi}\left(\dfrac{1}{r^{2}}-j\dfrac{1}{kr^{3}}\right)\cos\theta e^{-j k r} \\ E_{\theta}=\left(\dfrac{jk}{r}+\dfrac{1}{r^{2}}-j\dfrac{1}{kr^{3}}\right)\sin \theta e^{-jkr} \\ E_{\phi}=0\end{cases}
なお、\(Z_{o}\)は真空中の固有インピーダンス\(Z_{o}=\sqrt{\dfrac{\mu_{o}}{\varepsilon_{o}}}\)である。
(2)放射界の算出
(8)(9)式において、r→∞の極限を考える。
rが-2乗以上の項は、-1乗の項に対して十分小さいとみなせるため、下記になる。
\begin{cases}H_{r}=0 \\ H_{\theta}=0 \\ H_{\phi}=\dfrac{I_{o}l}{4 \pi}\left(j\dfrac{k}{r}\right) \sin \theta e^{-jkr}\end{cases}
\begin{cases}E_{r}=0 \\ E_{\theta}=\left(\dfrac{jk}{r}\right)\sin \theta e^{-jkr} \\ E_{\phi}=0\end{cases}
最後に
電磁ポテンシャル(ローレンツの条件)を用いて放射界を求める方法もありますが、今回は基本に忠実に解いてみました。
参考文献に、上記の方法で求める場合も記載してありますので、興味がある方は参照してみても良いかもしれません。
参考文献
電波工学 長谷川望 P62-71 (コロナ社)