下記の波形をPCM伝送したい。量子化ステップ数を256とする。
\begin{aligned}s(t)=A\cos(4000πt)+A\cos(2000πt)\end{aligned}
(1)ナイキストの標本化周波数を求めよ。
(2)標本化周波数でPCM伝送したときのビットレートを求めよ。
PCM伝送とは
信号を0,1の2元情報符号列に変換し、パルス波として送信する方式です。(Pulse Code Modulationの略です。)
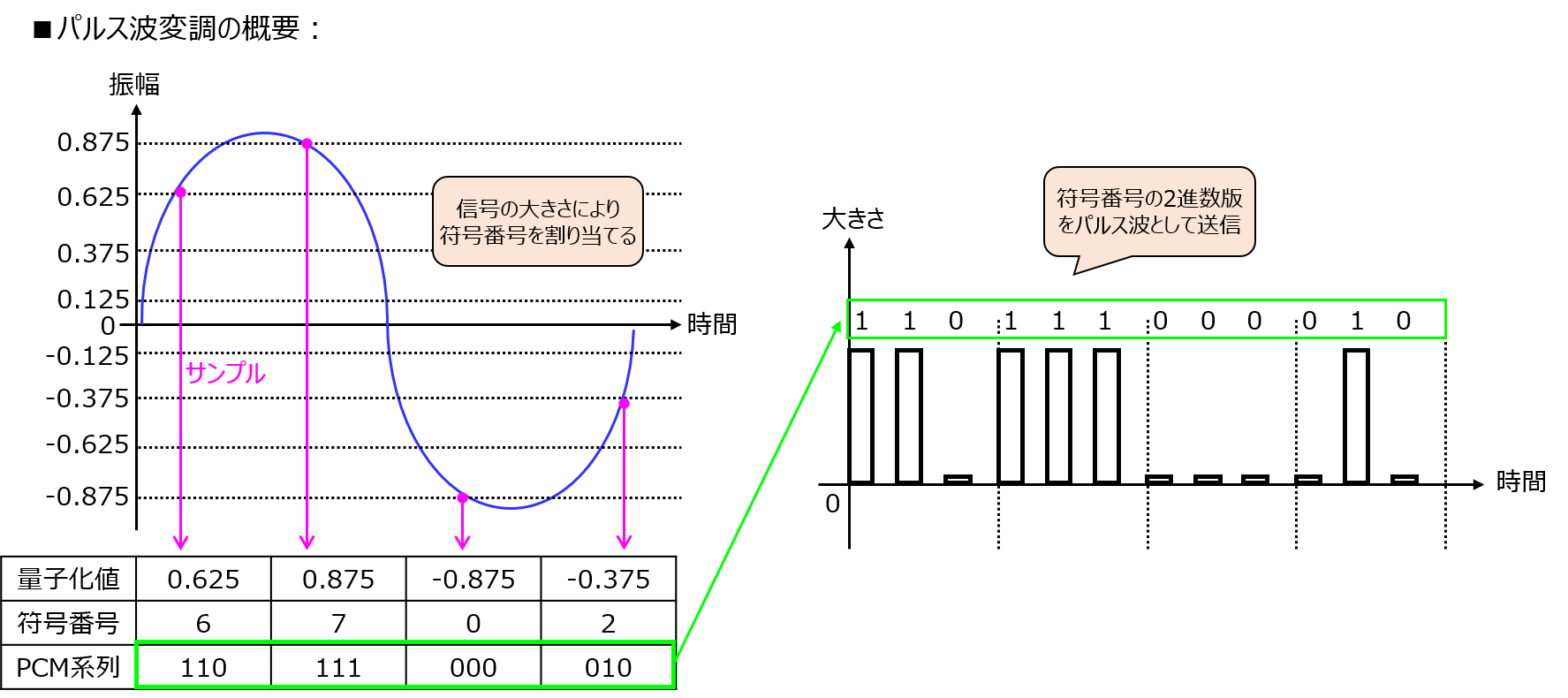
下記に、振幅1V正弦波を量子化ステップ数8でPCM伝送する場合を考えます。
量子化ステップ数とは、信号を表現できる細かさを言います。
ステップ数8ならば、-1V~1Vの2Vの範囲を1/8=0.125V刻みで表現できます。
正弦波は、時間ごとに電圧値が変化します。電圧値ごとに下記の符号番号を割り当てます。
| 電圧(V) | 符号番号 (10進数) | 符号番号 (2進数) |
| 0.875 | 7 | 111 |
| 0.625 | 6 | 110 |
| 0.375 | 5 | 101 |
| 0.125 | 4 | 100 |
| -0.125 | 3 | 011 |
| -0.375 | 2 | 010 |
| -0.625 | 1 | 001 |
| -0.825 | 0 | 000 |
この表に基づき、ある時間で電圧値0.625Vを送信したいときは、パルス波を110の順で送信すれば良いことが分かります。
受信側も、110が0.625Vであることが分かっていれば、0.625Vに復元することができます。
このように、共通のルールに基づいてパルス波を送信する通信方式をPCM伝送と言います。
補足:サンプリングした値の取り扱い
サンプリングした値から最も近い刻み点の値を採用します。
例えば、サンプリングした電圧値が0.7Vのときは、上の表だと0.625Vが一番近いです。
このため、0.625V(110)として送信します。
他、-0.4Vのときは、-0.375Vが一番近いことから、この値を(010)として送信します。
量子化サンプル数を増やした時の利点、欠点
利点:信号の分解能が細かくなり、より精度の高い通信ができる。
欠点:パルス波の長さが短くなり、周波数が大きくなる。雑音の影響を受けやすくなる。
利点について
前章の説明では、3bit符号=2^3=8であるため、信号を8つの段階でしか送信できませんでした。
しかし、4bitの場合は2^4=16より、16段階の送信ができます。
このように、bit数を増やすほど、信号のレベルを細かく分割でき、高精度の通信ができます。
欠点について
bit長が長くなると、単位時間あたりに送信しなければならないパルス波の数が多くなります。
一方で、パルス列の送信を完了する周期は固定です。
この制約を満たすため、一つのパルス波の波形を短く(細かく)する必要があります。
その結果、信号の周波数帯域が大きくなり、フィルタを通す帯域も広くなります。
一緒に通る雑音成分も大きくなるため、雑音の影響を受けやすくなります。
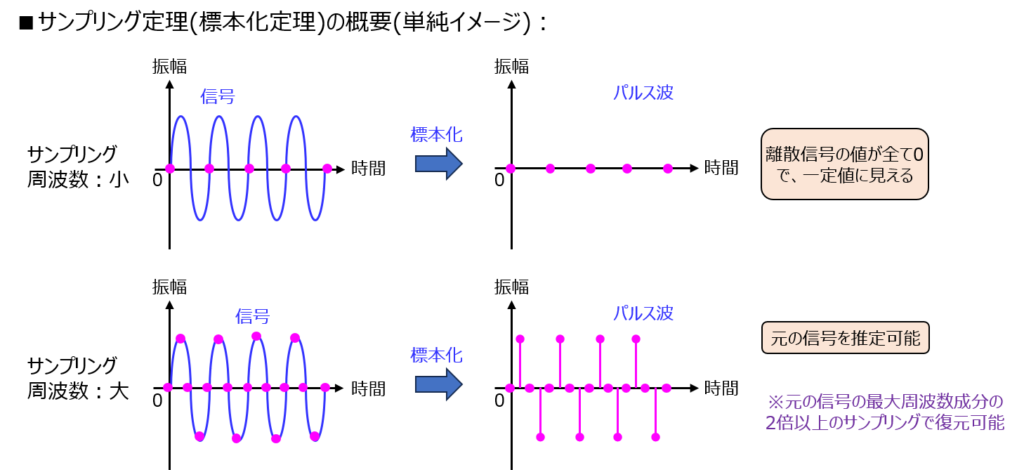
標本化定理
連続時間の信号を離散信号にサンプリングするとき、決まった周波数以上でデータを取らないと、正しく信号を復元できない事象を言います。
以前の記事にて類似の解説をしましたが、最大周波数成分が\(f_{m}\)の信号ならば、\(2f_{m}\)以上⇔周期\(T≦\frac{1}{2f_{m}}\)の必要があります。
信号の復元に最低限必要なサンプリング周波数を標本化周波数と言います。
感覚的な理解は以下です。
1.サンプリング周波数が大きいほど、周波数領域で立つスペクトルの間隔が開く。
2.標本化対象の信号が持つ周波数スペクトルを重ね合わせたとき、スペクトル同士が重ならなくなる。
3.スペクトル一つ分を低域通過フィルタに通すことで復元できる。
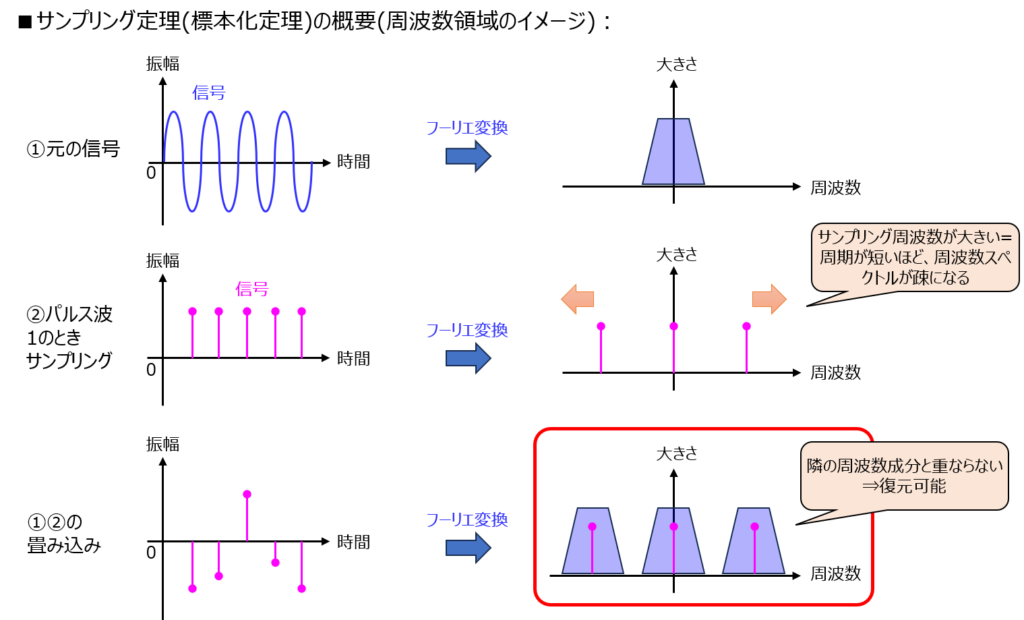
他、少し乱暴ですが、ある正弦波を周波数通りにサンプリングしたとき、一定値のものと見分けが付かない考え方もあります。(最初はこのくらいの理解で良いかもしれません。)
ビットレートとは
1秒間辺りに送信できるbit数を言います。
bit数は、前章のPCM伝送の原理から、パルス波の送信回数に依存します。
パルス波の送信回数は、信号を復元するための最低周波数(標本化周波数)分存在します。
標本化周波数に、量子化ステップ数をbit数にしたものを乗算することで、ビットレートを求められます。
(例えば、量子化ステップ数8だとすると、3bitで表現できます。これを標本化周波数と乗算することで、ビットレートが求まります。)
なお、単位は[bps]で、ネットワークの送受信速度を計測する際によく使用する単位になっています。
解答例
(1)ナイキストの標本化周波数
式(1)より、最高周波数成分は4000π=2π*2000だから、f=2000[Hz]
標本化定理より、この2倍の周波数でサンプリングすれば良い。
よって、ナイキスト周波数は、\(4000[Hz]\)
(2)ビットレート
量子化ステップ数が256のため、\(2^{8}=256\)。8bit符号である。
(1)より、ナイキスト周波数は4000[Hz]。1秒間に4000回8bit符号を送信するので
\begin{aligned}4000*8=32[kbit/sec]\end{aligned}