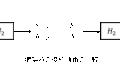周波数変調(FM)の原理と電力効率、復調方法

変調信号を\(s(t)\)とし、搬送波\(A\cos(2 \pi f_{c} t)\)により生成される角度変調波

\begin{aligned}g(t)=A\cos(\theta(t))\end{aligned}

を考える。ただし、\(s(t)\)の最大周波数を\(f_{s}\)とすると\(0<f_{s}<f_{c}\)であり、\(|s(t)|≦1\)とする。

(a)瞬時周波数\(f_{i}(t)\)を求め、周波数変調波\(g_{FM}(t)\)を導け。ただし、最大周波数偏移を\(\Delta f\)とする。
(b)\(g_{FM}(t)\)の式を用い、微分を用いた周波数変調波の復調原理を説明せよ。

東北大学 電気情報系 院試 専門科目 2019年3月 通信工学(2)より。記事向けの文言に一部改変

周波数変調(FM)とは

搬送波の周波数を変調信号\(s(t)\)に応じて変化させる方式です。(FM：Frequency Modulationの略です。)

以前の記事では、搬送波の振幅を変化させる振幅変調(AM)を説明しました。

振幅変調は、同一周波数帯でいくつもの信号を変調できる利点がありますが、電力効率が低いなどの欠点があります。

そこで、本記事では、もう一つの変調方法(周波数変調)を説明します。

原理

前節で述べたように、FM変調は、搬送波の周波数を変調する通信方式です。搬送波の周波数\(f_{c}\)に対しての差分を考え、\begin{aligned}f_{i}=f_{c}+\Delta f s(t)\end{aligned}と置きます。

\(\Delta f\)は最大周波数変位と言い、\(\Delta f s(t)\)は、瞬時周波数偏移と言います。

結局、搬送波の周波数\(f_{c}\)を加えた(1)式\(f_{i}\)が瞬時周波数になります。(問(1)の答え)

なお、瞬時周波数は、(1)式の\(\theta(t)\)を微分したものです。

ですので、FM変調波は、(2)式を積分し、(1)式に適用した形

\begin{aligned}g_{FM}(t)=A\cos\left(2\pi f_{c}t+2\pi\Delta f\int^{t}_{0}s(\tau)d\tau\right)\end{aligned}

になります。

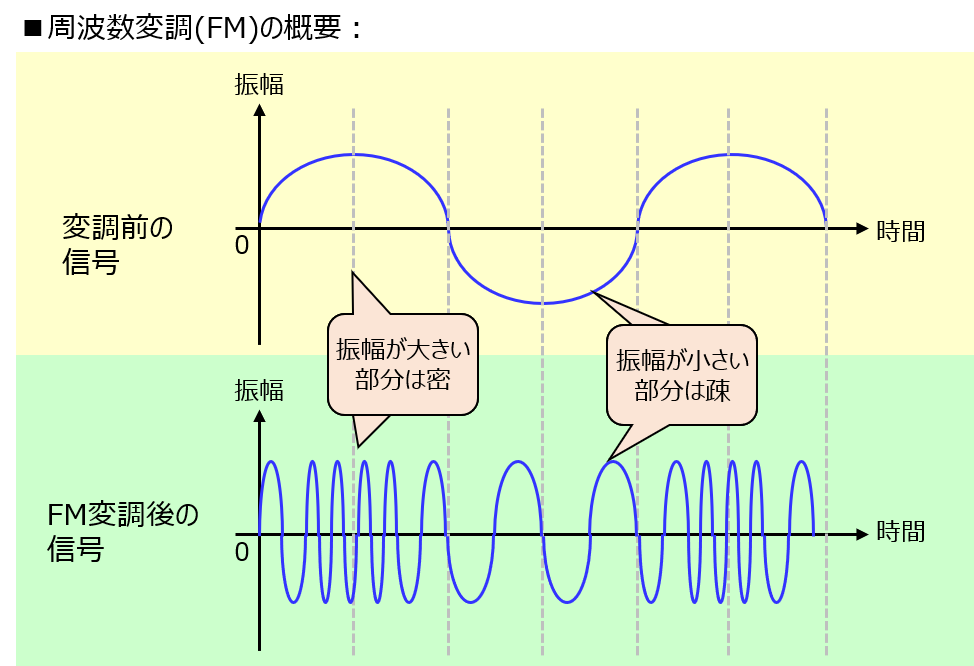
\(g_{FM}(t)\)を物理的なイメージで表すと下記になります。変調信号が小さいほど疎な波になり、大きいほど密な波になります。

電力効率

これは、問題形式で説明するには難しいので本節で取り上げます。高級な数学知識が必要です。

変調信号を\(s(t)=\cos(2 \pi f_{m}t)\)とするとき、(2)式は下記に変形できます。

\begin{aligned}g_{FM}(t)=A\cos(2\pi f_{c}t +m \sin(2 \pi f_{m}t))\end{aligned}

ただし、\(m\)はFM変調指数で\(\dfrac{\Delta f}{f_{m}}\)で表されます。

(4)式を複素関数を用いて表すと、下記のようになります。

\begin{aligned}g_{FM}(t)=Re[Ae^{j2 \pi f_{c}t}e^{j m \sin(2 \pi f_{m}t)}]\end{aligned}

ここで、下記の第1種ベッセル関数の公式を適用する。

\begin{aligned}e^{j m \sin(2 \pi f_{m}t)}=\sum ^{\infty }_{n=-\infty }J_{n}\left( m\right) e^{j2\pi nf_{m}t}\end{aligned}

これを(5)式に代入すると、下記のようになる。

\begin{aligned}g_{FM}(t)=A\sum ^{\infty }_{n=-\infty }J_{n}\left( m\right)\cos(2 \pi (f_{m}+nf)t)\end{aligned}

nは整数のため、厳密にいうと周波数帯域は無限大です。しかし、実用上は有限なため、以下の近似を行います。

第1種ベッセル関数は、mが大きくなると値が小さくなり、m<n-1では値が無視できる性質があります。よって、m+1より大きいnについて無視すると

\begin{aligned}B=2(m+1)f_{m}\end{aligned}

の帯域幅で電力は含まれます。(カーソン則と言います。)

無視できる部分を近似によって落としただけなので、一般的に、(7)式の帯域幅でも9割以上の電力が含まれています。(電力効率)

これは、振幅変調の最大電力効率33.3%に対し、大変優位な値となっています。

欠点

(6)式より、信号数を増やすほどnが大きくなり、必要な帯域幅が増えることです。

よって、一度に多数の相手と会話する航空管制には不向きな内容となっています。

解答例

(a)瞬時周波数と周波数変調波

前章の説明(原理)より瞬時周波数は(2)式で表される。

同じく、\(g_{FM}(t)\)は(3)式で表される。

(b)復調方法

(3)式に加法定理を用いると

\begin{aligned}g_{FM}(t)=A\cos(2 \pi f_{c} t+ 2 \pi )\cos(2 \pi \Delta f \int^{t}_{0}s(t) dt)-A\sin(2 \pi f_{c} t+ 2 \pi )\sin(2 \pi \Delta f \int^{t}_{0}s(t) dt)\end{aligned}

\(\Delta f << f_{c}\)より、\(\cos(\Delta f)\fallingdotseq 1\)、\(\sin(\Delta f)\fallingdotseq \Delta f\)に近似できるので

\begin{aligned}g_{FM}(t)=A\cos(2 \pi f_{c}t)-A2\pi f_{c}t \cdot 2\pi \Delta f \int^{t}_{0}s(t) dt\end{aligned}

右辺第1項が搬送波成分で、第2項が変調信号の項である。

(10)式を微分すると、第2項の積分部分の中身\(s(t)\)が抽出される。

よって、受信側で以下の操作をすることで復調信号が得られる

最後に

本問は、非常に計算が煩雑です。

試験問題として誘導付きになることは確実ですが、結果を知っていれば、さらなる時間短縮につながると思います。