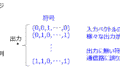\(S_{0},S_{1},S_{2},S_{3}\)をそれぞれ0.6,0.25,0.1,0.05の確率で発生する無記憶情報源について下記の問いに答えよ。
(1)2元ハフマン記号を用いて\(S_{0},S_{1},S_{2},S_{3}\)を符号化せよ。
(2)(1)で求めた符号の平均符号長を求めよ。
ハフマン符号とは
情報源を符号化する際に行う規則の一つです。
情報源を実際に伝送する際、文字を符号として置き換えて伝送する必要があります。
発生確率が低い情報源に対し、”0″,”1″などの一つの文字で完結する数値を何も考えず与えてしまうと、発生確率が高い情報源に対し”01″など2つの数値を割り当てることになり、受信側で受け取る符号長が長くなります。
符号長が長くなると、その分のbit割り当てが必要になり、処理時間が長くなる課題があります。
ここで利用するのが、ハフマン符号です。
これは、ある法則に基づいて、確率が高い文字ほど短い符号に割り当る手法です。情報源全体で送信する平均符号長が短くなる利点があります。
ハフマン符号化のルール
全体方針
左に符号化前の文字、右に符号化した後の数値を記載した樹形図を作成します。
符号化前の文字から出発し、途中で得た文字を右から並べていくことで、最終的な符号化値が分かります。
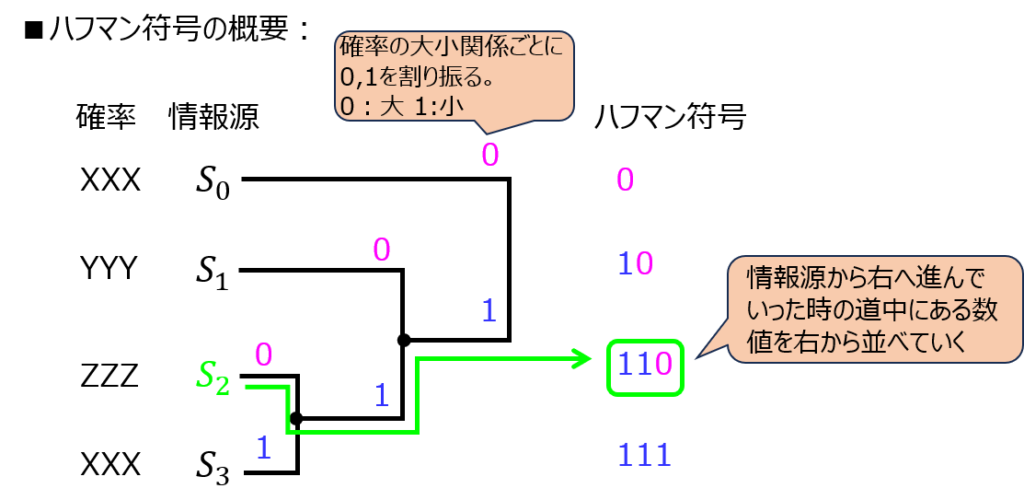
実際のルール
- 発生確率の大きい状態(文字)を左上から順に並べ、右に向く線を書く。
- 発生確率の小さい2つの状態を選び、線を合わせる。合計の確率を計算する。
- 2.で計算した確率に対し、発生確率が3番目に小さい状態との確率の大小関係を判定する。
- 確率が大きい側の状態を0、小さい側の状態を1とし、2.と同じく線を合わせる。
- 発生確率が4番目に低い状態に対しても同じことを繰り返す。
一言で説明すると、一番確率が小さい状態から出発し、2番目に小さい確率を持つ状態と符号化、合成を繰り返すわけですね。
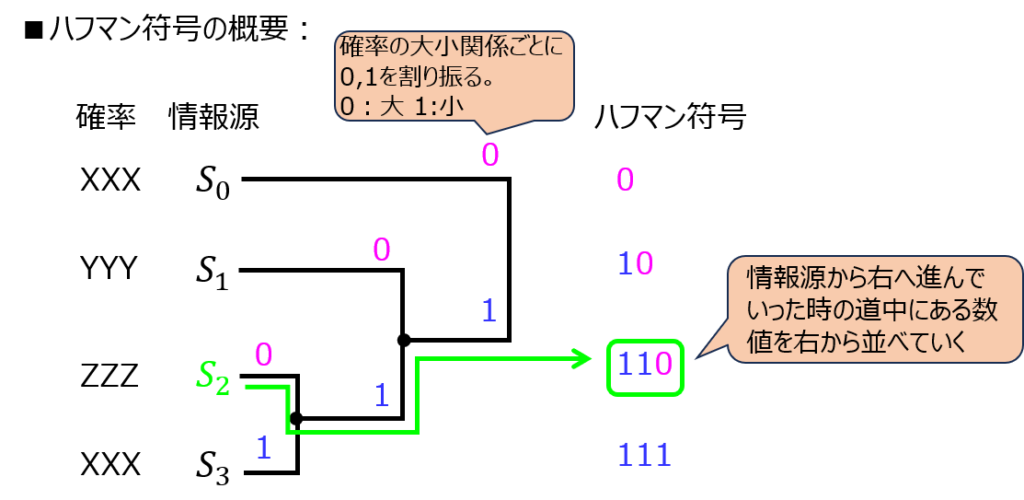
補足
前章のように、ハフマン符号化で作成する木については”直角”で書くことが多いです。これは、別の情報源とマージ、分岐した地点が明確に分かるようにするためです。どの教科書でも同じ書き方のため、試験の時でも慣例に習った方が良いと思います。
また、一般的に、確率の大きい情報源から符号0を付けていくことが多いですが、1を割り当てても良いです。(この場合、他の情報源に対しても符号1を割り当てていけば同じ結果になります。)
また、確率の等しい2つの情報源に対し割り当てるハフマン符号は順不同で良いです。(どのような組み合わせでも、平均符号長は変わらないため)
符号化の効率
無記憶情報源(1次)を0,1の2元符号化する際、平均符号長\(L\)とエントロピー\(H(S)\)の間には、下記の関係があります。
\begin{aligned}H(S)≦L<H(S)+1\end{aligned}
平均符号長は、自身の持つエントロピーより小さくならない。という意味になります。
意外と試験でも問われますので覚えておきましょう。(東大で出ました。)
他、N次拡大情報源をr元符号化する際も下記の式が成立します。
\begin{aligned}\dfrac{H(S)}{\log r}≦L<\dfrac{H(S)}{\log r}+\dfrac{1}{N}\end{aligned}
解答例
(1)ハフマン符号化
まず、\(S_{2},S_{3}\)の合成から始める。
\(S_{2}\)の確率の方が大きいので、\(S_{2}\)に0、\(S_{3}\)に1が付く。
また、確率の合計値は0.1+0.05=0.15である。
これを\(S_{1}\)と比較する。\(S_{1}\)の確率の方が大きいので、\(S_{1}\)に0。\(S_{2}+S_{3}\)に1が付く。
\(S_{1}~S_{3}\)の確率の合計値は0.4である。これは、\(S_{1}\)の確率より小さい。よって、ハフマン符号は下記図のようになる。
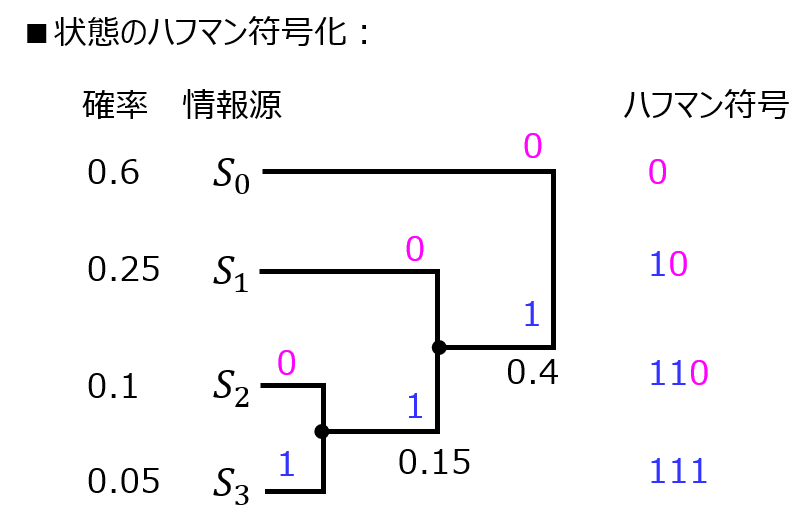
(2)平均符号長
(1)より、\(S_{0},S_{1},S_{2},S_{3},S_{4}\)のハフマン符号はそれぞれ(0,10,110,111)である。
これと発生確率を掛け合わせることで、求める平均符号長は
\begin{aligned}L&=1+0.6+2*0.25*3*0.1+3*0.05 \\ &=1.55\end{aligned}
最後に
ハフマン符号化、平均符号長の算出は、様々な大学の院試の頻出分野になります。
ただ、やることはシンプルです。本記事の問題を何も見ずに解けるようになりましょう。