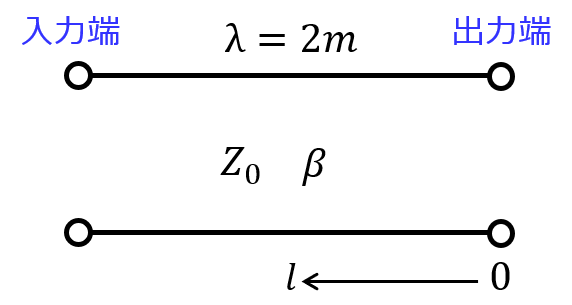
上図の無損失分布定数回路を考える。特性インピーダンスを\(Z_{0}=50[\Omega]\)とする。また、波長\(\lambda=2[m]\)とする。下図のスミスチャートを利用し、下記の問に答えよ。
(1)出力端に負荷\(Z_{L}=100-j100[\Omega]\)を接続した。受電端の反射係数\(\Gamma_{0}\)を求めよ。
(2)(1)のとき、\(l=1.25[m]\)の位置における反射係数\(\Gamma_{l}\)と駆動点インピーダンス\(Z_{l}\)を求めよ。
(3)出力端にある負荷\(Z_{L}\)を接続したとき、定在波比が3となり、\(l=1.1[m]\)から見た駆動点インピーダンスは純抵抗(リアクタンス無し)になった。考えられる\(Z_{L}\)の値を求めよ。
(4)受電端を短絡した。この時の駆動点インピーダンスは純虚数成分になった。考えられる\(l\)を求めよ。

はじめに
スミスチャートを利用し、分布定数回路の問題を解きます。以前までの記事は手計算で解いていきましたが、今回は図解的に解きます。
本記事で覚えたいこと
- \(\dfrac{Z_{L}}{Z_{0}}\)を計算し、規格化インピーダンスを求める。
- 規格化インピーダンスの実部、虚部をスミスチャートの軌跡にプロットする。
- 交点の半径が求める反射係数で、中心から交点へ直線を引いた外周円との交点が求める角度
- スミスチャートは半波長で一周する。
- 出力端⇒入力端方向へ考えるとき、時計回り、入力端⇒出力端で見るとき、反時計周り
スミスチャートとは
反射係数の式を利用し、ある位置における駆動点インピーダンスを複雑な計算無しで求められるよう図式化したものです。反射係数について、以前の記事でお話ししたように、下記の関係があります。
\begin{eqnarray}\Gamma =\dfrac{Z_{x}-Z_{0}}{Z_{x}+Z_{0}}=\dfrac{\frac{Z_{x}}{Z_{0}}-1}{\frac{Z_{x}}{Z_{0}}+1}=\dfrac{Z’-1}{Z’+1}\end{eqnarray}
\(Z_{x}\)は、駆動点インピーダンスです。\(Z_{0}\)は固定のため、反射係数の絶対値は最大1であることがわかります。
変数の個数の関係により、反射係数が分かれば、\(Z_{x}\)も分かります。これより、取りうる全てのインピーダンスを反射係数に変換して、単位円内に表示したものになります。
実際に問題で解くうえでは、\(Z_{x}\)を\(Z_{0}\)で割った規格化インピーダンス\(Z’\)を使用します。
反射係数の極座標表示\(\Gamma=|\Gamma|e^{j\theta}\)を考えると、\(\Gamma=0\)が単位円の中心。\(|\Gamma|=1\)が外周円になります。
横軸が実数成分、縦軸が虚数成分です。スミスチャートの右側の実軸との交点が定在波比にあたります。
スミスチャートの1周分は半波長分です。理由は、入射波と反射波の位相差によります。入射波の位相をaとすると、反射波の位相は-aです。入射波と反射波の合成波を考えると、入射波の位相が180度になれば、反射波の分と合わせて全体360度が取れます。
定在波も上記のような振る舞いになっています。腹と腹の間隔は半波長です。
5.については、(2),(3)で用います。
解答例
(1)受電端の反射係数
まず、規格化インピーダンスは
\begin{eqnarray}Z’_{L}=\dfrac{100-j100}{50}=2-j2\end{eqnarray}
であるので、スミスチャートの(2,-j2)に対応する軌跡をプロットすると以下のようになる。
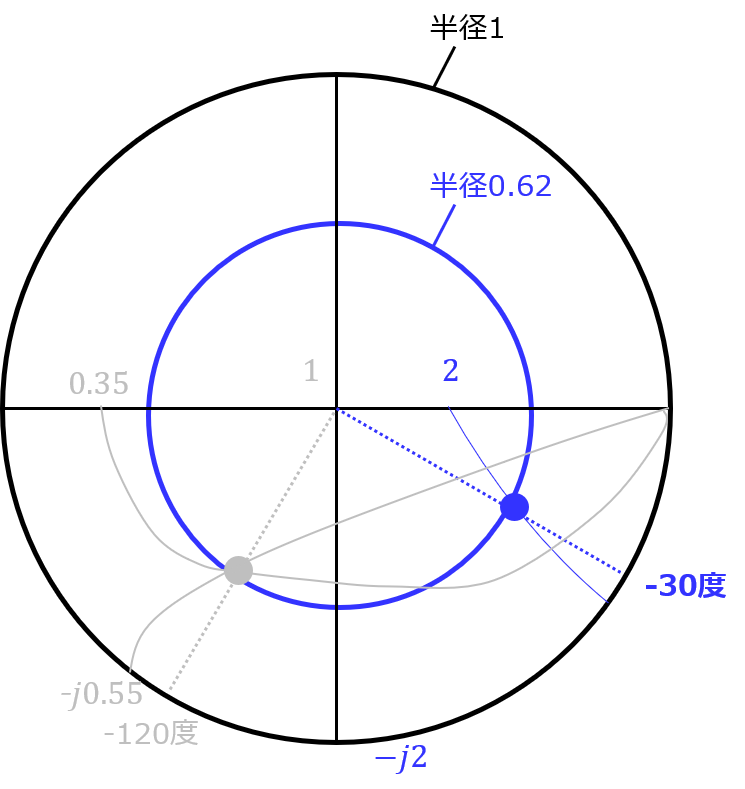
青点が交点であり、これの半径は0.62、中心と交点の2点を結ぶ線に対応する角度は-30度
よって求める反射係数は\begin{eqnarray}\Gamma_{0}=0.62 \angle-30\end{eqnarray}
(2)\(l=1.25[m]\)の位置における反射係数\(\Gamma_{l}\)と駆動点インピーダンス\(Z_{l}\)
\(\lambda=2[m]\)より、半波長は1m。これでスミスチャート1周分(360度)に対応する。
\(l=1.25[m]\)のとき、1周と0.25周。(1)で求めたインピーダンスは出力端であるので、入力端方向へ考える。青点から90度時計回りに動かした点を考えればよい。
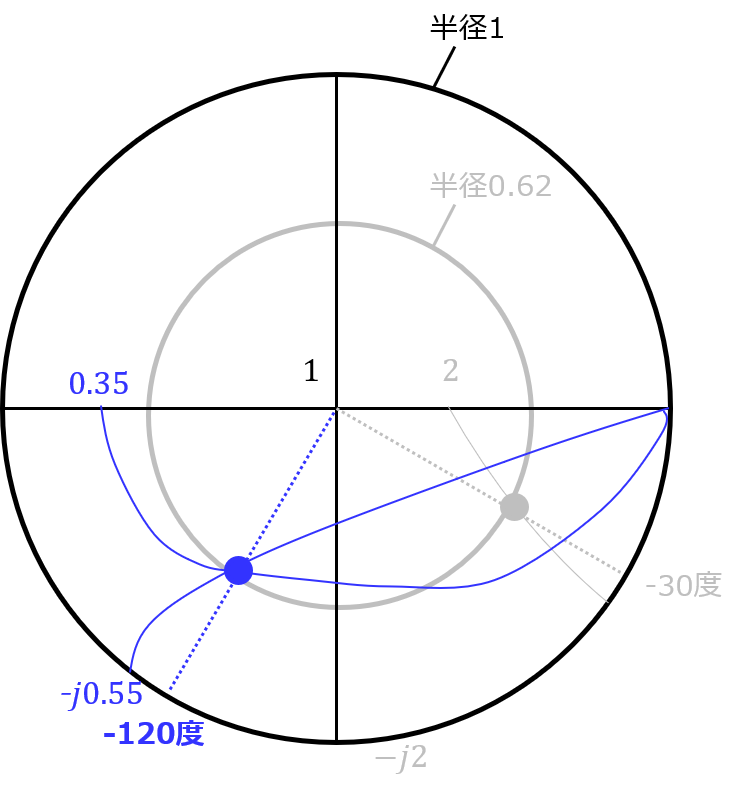
半径は変わらないので、反射係数は\begin{eqnarray}\Gamma_{l}=0.62 \angle-120\end{eqnarray}
青点に対応する規格化インピーダンスは、\begin{eqnarray}Z’_{in}=0.35-j0.55\end{eqnarray}
これに、特性インピーダンス\(50[\Omega]\)をかけると、求める駆動点インピーダンスは
\begin{eqnarray}Z_{l}=50(0.35-j0.55)\end{eqnarray}
(3)\(Z_{L}\)の値
\(l=1.1[m]\)で、入力端⇒出力端方向で考えるので、1周と0.1回転=36度反時計回りに回転した点を考えれば良い。
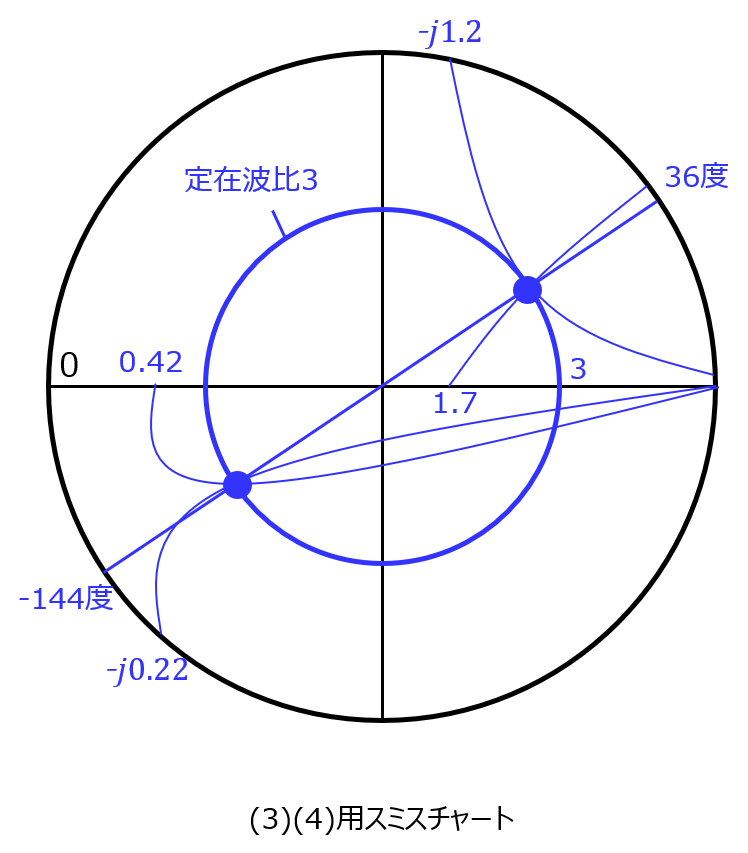
よって、考えられるインピーダンスは、下記2通り
\begin{eqnarray}Z_{L}=1.7+j1.2 , 0.42-j0.22\end{eqnarray}
(4)受電端を短絡したときの長さ\(l\)
短絡したとき、出力端のインピーダンスは\(0[\Omega]\)
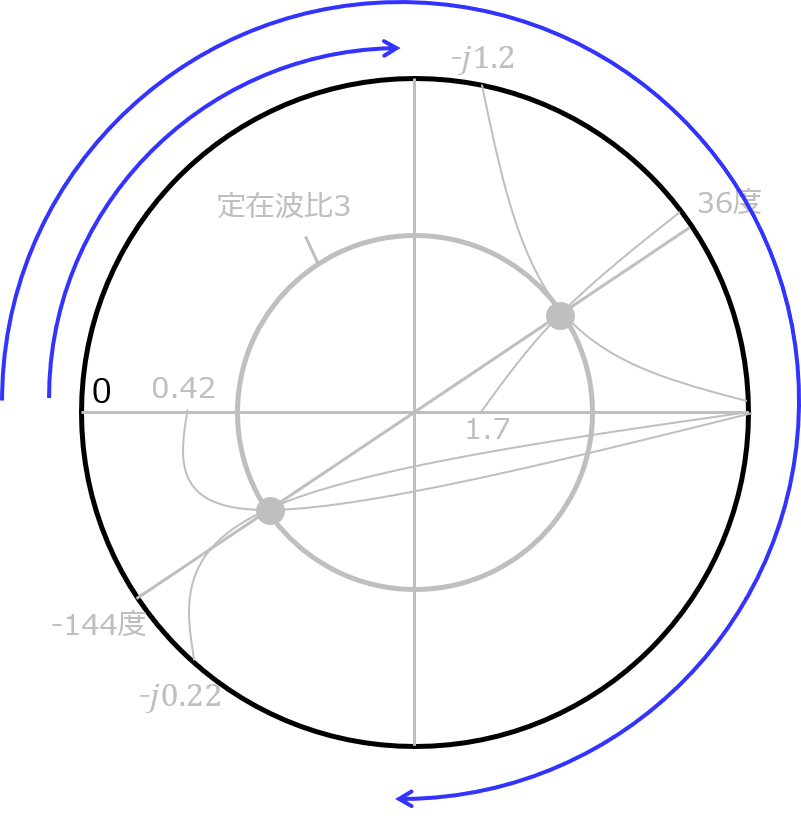
そこから、長さ\(l\)分だけ離れるごとに位相差が付いていく。
純虚数成分になるとき、90度、270度になると考えられるので、考えられる\(l\)は
\(l=0.25n,0.75n [m]\) (n:自然数)
補足(定在波法)
本問のように、反射係数が分かれば、出力端に接続するインピーダンス\(Z_{L}\)の値が分かります。
スミスチャートで図式的に解く方法を紹介しましたが、定在波法なる方法もあります。
反射係数の式(1)を変形し、下記のように\(Z_{L}\)を求められます。
\begin{eqnarray}Z_{L}=Z_{0}\dfrac{1-j\Gamma \tan \left( \dfrac{2\pi l_{min}}{\lambda }\right) }{\Gamma -j\tan \left( \dfrac{2\pi l_{min}}{\lambda }\right) }\end{eqnarray}
なお、\(l_{min}\)は、出力端から腹までの最小距離です。
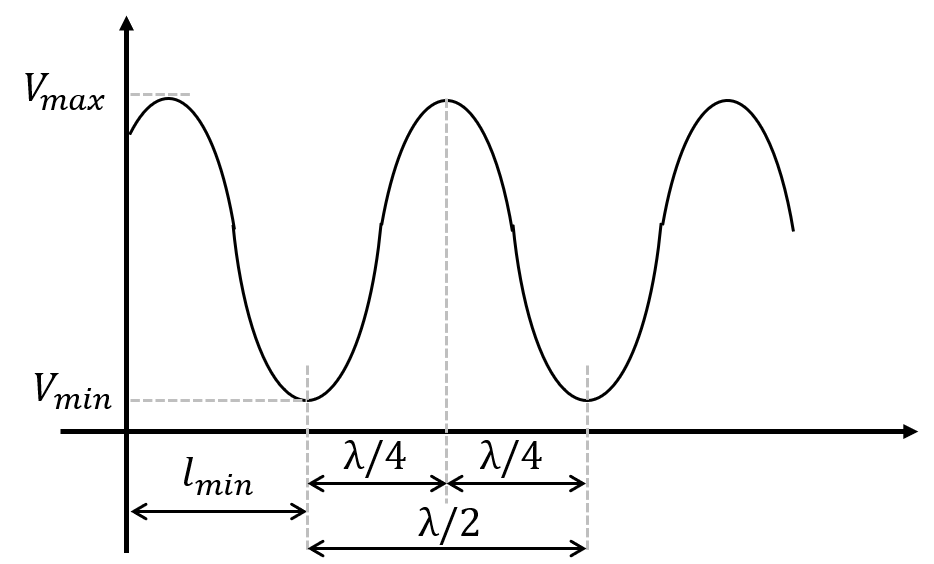
実験的に\(l_{min}\)が分かれば、後は回路の条件、波長の長さから\(Z_{L}\)が求まります。
最後に
本問では、今までの問題と異なる解き方をしました。別の切り口で考えることで、分布定数回路に対する理解が深まると幸いです。
参考文献
アンテナ工学ハンドブック:電子情報通信学会 P53
電波工学:長谷川望(著) P11