下記の力学運動系システムの伝達関数を求めよ。ただし、変数xの初期値は0とする。また、\(K_{i}\)はばね定数。\(D_{i}\)は減衰定数。物体の質量を\(M_{i}\)とする。
(1)ダンパ\(D_{1}\)と直列にばね定数\(K\)、ダンパ\(D_{2}\)が並列で接続された系。入力\(x(t)\)に対する出力\(y(t)\)。
(2)質量\(M\)、\(m\)の物体がダンパ\(D\)、ばね定数\(K\)のばねに接続されている系。\(M\)に外力\(f(t)\)を与えた時の\(m\)の変位\(y(t)\)

力学系システムと伝達関数
ある制御対象を目標値に制御するためには、制御対象を適切な数学モデルに変換する必要があります。例えば、下記のような運動系(ばね-ダンパ)を考えます。ダンパとは、振動・運動エネルギーを減衰する機械部品です。
外力を\(f(t)\)、質量\(M\)を持つ物体の変位を\(x(t)\)とすると、青矢印の力がかかります。

これより、運動方程式は
\begin{aligned}f(t)=M\dfrac{d^{2}x}{dt^{2}}+D\dfrac{dx}{dt}+Kx(t)\end{aligned}
変位をある一定の値に制御したい。と考えた時、上式では\(x(t)\)で対象の変数を表しています。よって、これを目標値に合うように計算することで、適切に制御できると考えられます。
今日では、計算機の発達により、微分方程式のまま近似計算を用いて制御検討できるようになりました。しかし、昔はそのようなことはできませんでした。代替手段として、微分方程式をラプラス変換をし、微分項、積分項を\(s\)の次数に置き換え、微分積分項が存在しない式に変換。計算していました。
その名残で、大学講義で制御工学を習う時は、最初に古典制御を扱います。ラプラス変換を用いて計算できるモデルを対象としています。
実際に、(1)式をラプラス変換すると下記になります。2次の微分項は\(s^{2}\)、1次は\(s\)とすると、下記になります。
\begin{aligned}F(s)=Ms^{2}X(s)+DsX(s)+KX(s)\end{aligned}
以上より、伝達関数\(G(s)=\dfrac{X(s)}{F(s)}\)は下記のようになります。
\begin{aligned}G(s)=\dfrac{1}{Ms^{2}+Ds+K}\end{aligned}
後は、質量\(M\)に応じて、減衰定数\(D\)、ばね定数\(K\)を選び、制御系の最適設計ができます。
本記事では、様々な運動系の伝達関数を考えていきます。機械力学と密接な関係にあるため、電気系出身者よりは機械系の方が太刀打ちしやすい問題内容です。
解答例
(1)ダンパとばねの直列結合系
系にかかる力を図示すると、青矢印のようになる。

ダンパ\(D_{1}\)にかかる力\(F_{1}\)は、
\begin{aligned}F_{1}=D_{1}\dfrac{dy}{dt}\end{aligned}
ばね定数\(K\)、ダンパ\(D_{2}\)の系にかかる力\(F_{2}\)は、相対変位が\(x(t)-y(t)\)であることに注意すると
\begin{aligned}F_{2}=K(x(t)-y(t))+D_{2}\dfrac{d(x(t)-y(t))}{dt}\end{aligned}
\(F_{1},F_{2}\)の力は等しいので
\begin{aligned}D_{1}\dfrac{dy}{dt}=K(x(t)-y(t))+D_{2}\dfrac{d(x(t)-y(t))}{dt}\end{aligned}
これをラプラス変換し、\(G(s)=\dfrac{Y(s)}{X(s)}\)を考えると
\begin{aligned}D_{1}sY(s)=K(X(s)-Y(s))+D_{2}s(X(s)-Y(s))\end{aligned}
\begin{aligned}G(s)=\dfrac{D_{2}s+K}{(D_{1}+D_{2})s+K}\end{aligned}
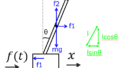
(2)2質量系の伝達関数
\(M\)、\(m\)にかかる力を青矢印、緑矢印で図示すると下記のようになる。

運動方程式は
\begin{cases}f(t)=M\dfrac{d^{2}x}{dt^{2}}+K(x(t)-y(t))+D\left(\dfrac{d(x(t)-y(t))}{dt}\right) \\ m\dfrac{d^{2}y}{dt^{2}}= K(y(t)-x(t))+D\left(\dfrac{d(y(t)-x(t))}{dt}\right)\end{cases}
上式をラプラス変換し
\begin{cases}F(s)=Ms^{2}+Ds(X(s)-Y(s))+K(X(s)-Y(s)) \\ ms^{2}Y(s)=Ds(X(s)-Y(s))-K(X(s)-Y(s))\end{cases}
以上より、求める伝達関数は、\(X(s)\)を消去することで
\begin{aligned}G(s)&=\dfrac{Y(s)}{F(s)} \\ &=\dfrac{Ds+K}{s^{2}(Mms^{2}+(M+m)Ds+K(M+m))}\end{aligned}
最後に
本問は、電気系と言うよりは機械系の院試で出てきがちですが、名工大のように、電気系の院試でも出題される場合があります。機械要素を知る機会にもなり、社会に入ってからも役立ちます。