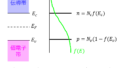
電気伝導の項目
ドリフト電流と拡散電流に大別されます。
ドリフト電流は、半導体内の電場によって流れる電流です。
拡散電流は、半導体内の電子の濃度勾配によって流れる電流です。
下記にて、詳しく解説していきます。
ドリフト電流の特性
電子のドリフト移動度を\(\mu_{n}\)、電場を\(E\)とすると、電子の平均速度\(v_{d}\)は下記の式で表すことができます。
\begin{eqnarray}v_{d}=-\mu _{n}E\end{eqnarray}
ただし、現実的には散乱が発生します。これは、結晶格子内を電子が移動する際、下記の影響により電子の速度が変化する事象です。
- 結晶格子の振動により、原子の作る電場が局所的に変動する
- イオン化した不純物が半導体内に存在し、そのクーロン力により速度変動する
- 半導体内の中性不純物により、電場が局所的に変動する

特に2.が重要です。これは、次節で説明します。
散乱と散乱の間の距離を平均自由行程\(\lambda\)、平均速度を\(v\)平均時間を\(\tau\)とすると、以下の運動方程式で表すことができます。
\begin{eqnarray}m\dfrac{dv}{dt}=-eE-m\dfrac{v}{\tau }\end{eqnarray}
これをラプラス変換を利用し、解くことで以下の式を導出できます。
\begin{aligned}msV\left( s\right) =-\dfrac{eE}{5}-\dfrac{m}{\tau }V\left( s\right) \\ V\left( s\right) =\dfrac{eE}{m}\dfrac{1}{s\left( s+\dfrac{1}{\tau }\right) }\\ v\left( t\right) =-\dfrac{e}{m}TE\left( 1-\exp \left(-\frac{t}{\tau} \right) \right) \end{aligned}
\(t→∞\)の極限を考えると、
\begin{eqnarray}v=-\dfrac{e}{m}\tau E\end{eqnarray}
これを(1)式を比較すると、電子移動度は下記の関係で表される。
\begin{eqnarray}\mu = \dfrac{e}{m}\tau \end{eqnarray}
電流密度を\(J\)とすると、下記の式で表すことができる。
\begin{eqnarray}J=-env=en\mu E=\sigma E\end{eqnarray}
ただし、\(\sigma\)は導電率で、下記の式で表すことができる。
\begin{eqnarray}\sigma=en\mu\end{eqnarray}
電子についての関係を示してきましたが、正孔についても同じ関係式が成立します。
よって、正孔分も加味すると(7)式は下記のように表すことができます。
\begin{eqnarray}\sigma=e(n\mu_{n}+p\mu_{p})\end{eqnarray}
ただし、\(\mu_{n}\)は電子移動度、\(\mu_{p}\)は正孔移動度です。
不純物濃度と移動度の関係
前節の説明は、散乱が理想的だった場合の話です。
実際は、半導体内の不純物の濃度によって散乱の程度も変わります。温度にもよりますが、半導体内の移動度は下記の関係になります。

低温領域では、熱の影響が小さいため、不純物から発生する電場の変化による散乱の影響を受けます。
高温領域では、熱による格子振動の散乱が支配的になります。よって、不純物による散乱はあまり関係なくなります。
拡散電流の特性
定義から、電子、正孔の拡散電流は以下の式で表すことができます。
\begin{cases}J_{n}=eD_{n}\dfrac{dn}{dx}\\
J_{p}=-eD_{p}\dfrac{dp}{dx}\end{cases}
ただし、\(D_{n}\)は電子の拡散係数、\(D_{p}\)は正孔の拡散係数を示します。微分項で濃度を微分していることから、拡散電流を表していることが分かります。
電子密度をマクスウェル・ボルツマン分布により、下記の式でおきます。
\begin{eqnarray}n\left( x\right) =C\exp \left( -\dfrac{e\overline{V}\left( x\right) }{kT}\right)\end{eqnarray}
ただし、Cは定数です。上式をxで微分すると以下の式が成立します。
\begin{eqnarray}\dfrac{dn}{dx}=-\dfrac{Ce}{kT}\exp \left( -\dfrac{eV(x)}{kT}\right)\dfrac{dV(x)}{dx}=\dfrac{e}{kT}n(x)E\end{eqnarray}
熱平衡状態のときドリフト電流と拡散電流は等しいので、下記の関係が成立します。
\begin{eqnarray}en(x)\mu_{n}E=eD_{n}\dfrac{dn}{dx}=\dfrac{e}{kT}n(x)E\end{eqnarray}
ホール効果を利用した移動度の測定
前章まで、電子の移動度について説明してきました。本節では、実験的に移動度を求める方法を説明します。
ホール効果とは
半導体に電流、磁場をかけると半導体内で電場が発生する現象です。これを利用し、半導体の物性値を計測しています。
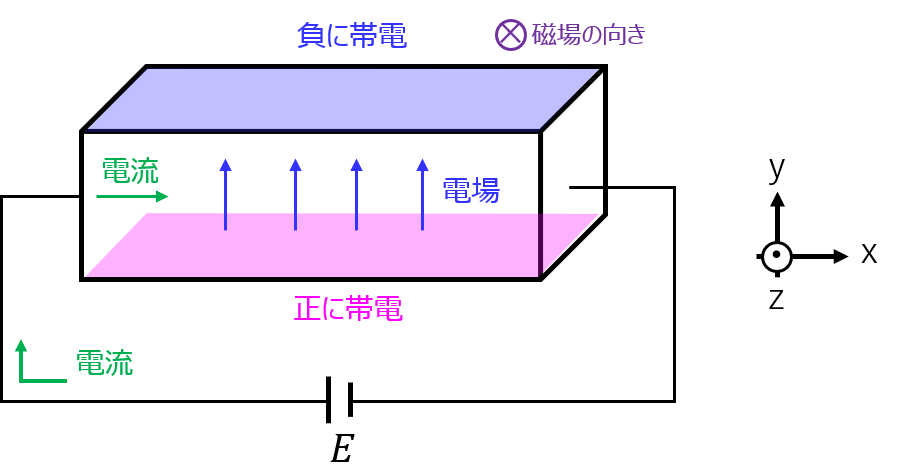
半導体の+x方向に電流を流し、-z方向に磁場を印可する場合を考えます。
電子は-x方向に流れるため、ローレンツ力が+y方向に働きます。これにより、電子が+y方向に帯電するため、電場が+y方向に発生します。
電場により発生する電位差を\(V_{H}\)とし、ローレンツ力とクーロン力が等しいとき、下記の関係が成立します。
\begin{eqnarray}evB=\dfrac{eV_{H}}{d}\end{eqnarray}
左辺がローレンツ力を示し、右辺がクーロン力を示します。なお、電場は一定です。
これを簡単化すると
\begin{eqnarray}I=envwd\end{eqnarray}
\begin{eqnarray}V_{H}=\dfrac{IB}{enW}=R_{H}\dfrac{IB}{W}\end{eqnarray}
\(\sigma=en\mu\)であるため、結局電子移動度は下記の式で表すことができます。
\begin{eqnarray}\mu_{H}=\dfrac{\sigma}{en}\end{eqnarray}
最後に
院試では、本記事の導出過程を問われることがあります。文章の誘導に乗って進めることがありますので、出題意図も理解しながら解き進めるようにしましょう。
参考文献
半導体デバイス 松波 弘之 (著), 吉本 昌弘 (著) 第2章