相互情報量の意味、例題と通信路容量との関係

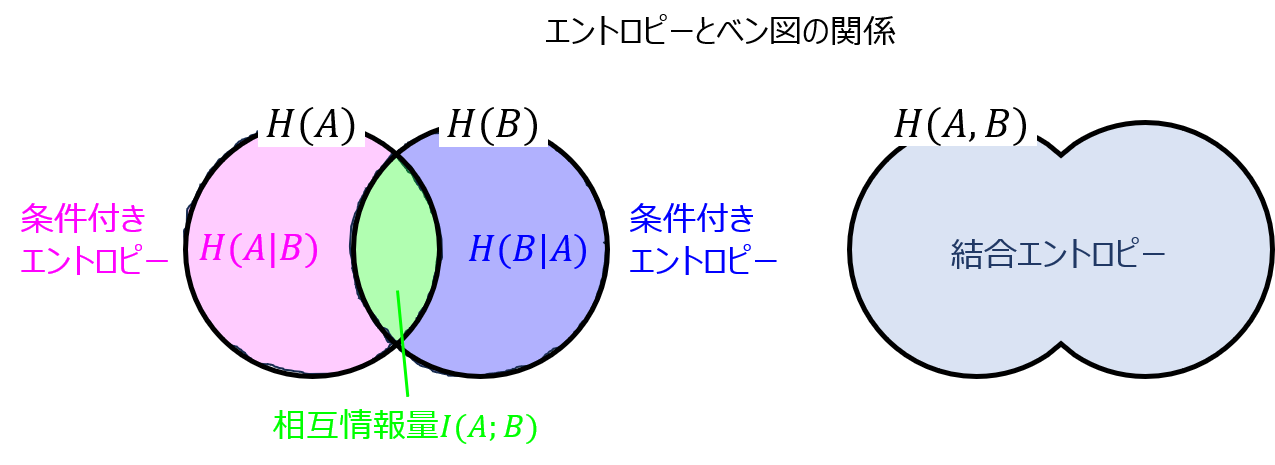
相互情報量とは

事象A,Bの持つエントロピーの相互関係を示します。

下記にてベン図を示します。

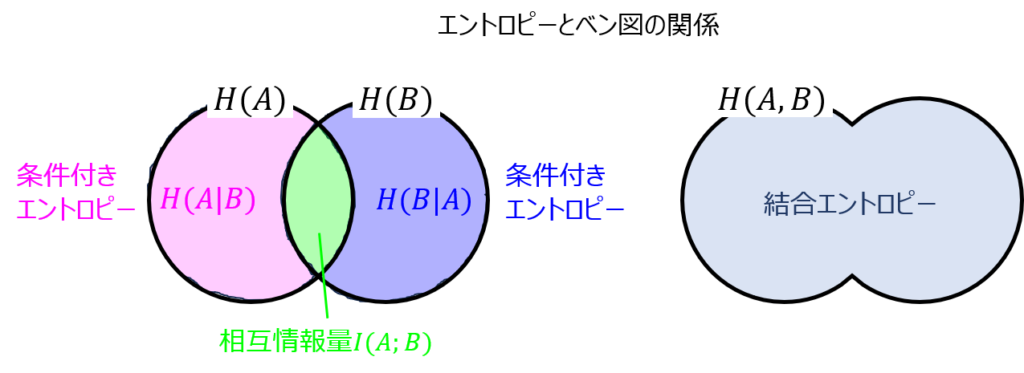
事象Aの持つエントロピーとBの持つエントロピーの共通事象部分を相互情報量と言います。

事象Bが発生していることが分かった上での事象Aのエントロピーを\(H(A|B)\)とすると、下記の関係式で表せます。

1.について、負になる相互情報量は無いです。相互情報量を得たことで、元の事象Aのエントロピーは増えることは無いことが分かります。(ベン図で見ると分かりやすいです。)

2.について、下記の解釈ができます。

つまり、事象Aのエントロピーが、\(H(A)=100\)とし、事象Bが分かった上でのAの条件付きエントロピーが\(H(A|B)=90\)だとすると、

相互情報量は\(I(A;B)=10\)となります。事象Bが分かったことで、Aの不確定性が10下がった。と言うことが分かります。

条件付きエントロピーの計算

前章では、相互情報量\(I(A;B)\)の計算に条件付きエントロピー\(H(A|B)\)を使用することが分かりました。

では、\(H(A|B)\)はどのようにして求めるのでしょうか。

相互情報量は未知であることが多く、前章の関係式は使用できません。

そこで、下記の式を使用します。

\begin{aligned}H\left( A| B\right) =-\sum_{A}\sum_{B}P\left( a,b\right) \log P\left( a|b\right)\end{aligned}

事象A,Bを構成する要素の取り得る確率に対するエントロピーを総当たりで足していけば、条件付きエントロピーを求められます。

注意点として、logの外では結合確率。logの中は条件付き確率を代入する必要があります。

これにさえ気を付ければ、\(H(A|B)\)が求まり、\(I(A;B)\)も求まるということですね。

相互情報量と通信路容量

通信路容量とは

ある通信路に情報源を伝送したときに伝送できる情報量の最大値を言います。

例えば、下記の通信路を考えます。入力を\(X\)、出力を\(Y\)とすると、通信路容量\(C\)は

\begin{aligned}C=max\lbrace I(X;Y)\rbrace\end{aligned}

で表されます。

通信路容量の最大は1で、最小は0です。大きいほど、伝送可能な情報量が大きいため、通信路として優れている。と言えます。

加法的2元通信路の通信路容量

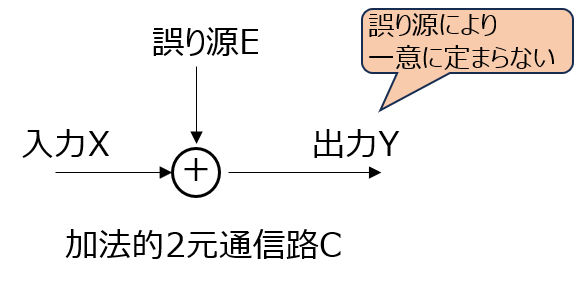
誤り源Eのエントロピーを\(H(E)\)とすると、下記で表されます。

\begin{aligned}C=1-H(E)\end{aligned}

証明

通信路の図より、相互情報量\(I(X;Y)\)は

\begin{aligned}I(X;Y)&=H(Y)-H(Y|X) \\ &=H(Y)-H(X \oplus E|X) \\ &=H(Y)-H(E|X)\end{aligned}

誤り源Eと入力Xは独立のため、\(H(E|X)=H(E)\)となる。
また、(2)式より相互情報量の最大値を考える必要があるので、\(H(Y)=1\)とする。

このとき、(3)式が成立する。

解答例

(1)エントロピー\(H(A)\)

サイコロは1~6の目を取り、全て確率は等しい。

1の目が出た時のエントロピーは\(H(a=1)=-\dfrac{1}{6}\log_{2}\dfrac{1}{6}\)

2以上の目に対しても同じのため、結果を6倍すれば良く

\begin{aligned}H(A)&=-\dfrac{1}{6}*6\log_{2}\dfrac{1}{6} \\ &=\log_{2}6\end{aligned}

(2)条件付きエントロピー

事象Bが4以上かつ事象Aに4が出る確率は\(P(a=4,b≧4)=\dfrac{1}{6}\)

事象Bが4以上であることが分かっている上で、事象Aに4の数値が出る確率は\(P(a=4|b≧4)=\dfrac{1}{3}\)

事象Bが4以上かつ事象Aに5,6が出る確率 および 事象Bが3以下かつ事象Aに1,2,3が出る確率も上記と同じ考え方をすれば良いので、(1)式から

\begin{aligned}H(A|B)&=-\sum_{A}\sum_{B}\dfrac{1}{6}\log_{2}\frac{1}{3} \\ &=6*\dfrac{1}{6}\log_{2}\frac{1}{3} \\ &=\log_{2}3[bit]\end{aligned}

(3)相互情報量

相互情報量の関係式により

\begin{aligned}I(A;B)&=\log_{2}6-\log_{2}3=1[bit]\end{aligned}

(4)通信路容量

ビット誤り率1/3の場合のエントロピー、誤りなく送信できる確率2/3の事象を合わせたエントロピー\(H(E)\)を考える。(3)式より

\begin{aligned}C&=1-H(E) \\ &=1+\frac{1}{3}\log_{2}\frac{1}{3}+\frac{2}{3}\log_{2}\frac{2}{3}\end{aligned}

最後に

相互情報量を求めるために、事象A,Bのそれぞれのエントロピーおよび、条件付き確率を前段で求めることが多いです。

ぜひ、試験問題全体を見渡し、相互情報量を求める問題が出ているときは、各事象のエントロピーから考える癖を付けましょう。