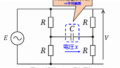
下記の図に示すように、質量Mの台車の上に質量m、長さ2lの棒が乗っている倒立振子を考える。この系が\(\theta=0\)の近傍で動作しているとき、下記の問(1)(2)を答えよ。ただし、棒については中心点を重心とする。また、\(\sin \theta \fallingdotseq \theta,\cos \fallingdotseq 1\)を用いて良い。
(1)入力\(f(t)\)に対する出力\(\theta\)の伝達関数\(G(s)\)を求めよ。
(2)入力\(f(t)\),状態変数\(\theta,\theta’,x,x’\)に対する下記の状態方程式を求めよ。
\begin{aligned}x=Ax+bu\end{aligned}

倒立振子とは
重心が支点の上にある運動系を指しています。上記の図のように、長さ\(2l\)の振子は、台車との接点を始点としています。重心は支点の上に存在するため、少しの外乱で横に傾いた時、重力に引っ張られて何もしないと倒れてしまいます。
このような事象を防止するため、台車が左右に動くことでバランスを取ろうとします。制御工学の安定性を検討する際、よく使用するモデルです。九大の院試でも出題されたことがあります。
伝達関数、状態方程式の求め方
以前の記事で類題を説明したように、下記の手順で解くことができます。
- 伝達関数の求め方
- 系の運動方程式を立式し、ラプラス変換する。
- ラプラス変換した式のうち、未知数を削除し、入力と出力の関係式を立てる。
- 入力と出力の比を取り、伝達関数を求める。
- 状態方程式の求め方
- 系の運動方程式を立式する。(ラプラス変換はしなくて良い)
- 状態変数の微分項に対する定常項の関係を立式し、行列表示する。
結局、運動方程式を適切に変形していくことに尽きます。こればかりは、多くの問題を解いて慣れていくしかありません。(電気回路における状態方程式の立て方も過去の記事で解説しています。合わせて確認してみると良いです。)
倒立振子の場合は下記のようになりますので、是非練習してみましょう。
解答例
(1)倒立振子の伝達関数
物体にかかる力を図示すると、以下のようになる。
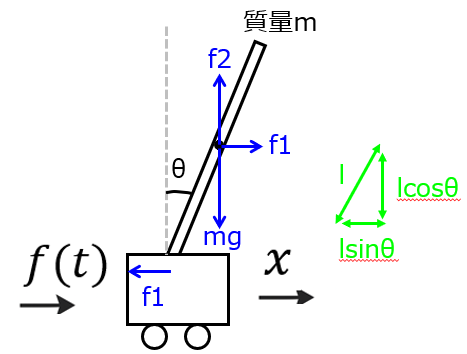
これより、支点に加わる水平方向の力を\(f_{1}\)、垂直方向の力を\(f_{2}\)は
\begin{cases}f_{1}=m\dfrac{d^{2}}{dt^{2}}(x+l \sin \theta) \\ f_{2}=mg+m\dfrac{d^{2}}{dt^{2}}(l \cos \theta) \end{cases}
これを用いて、運動方程式は下記のようになる。
\begin{cases}M\dfrac{d^{2}x}{dt^{2}}=f(t)-f_{1} \\ I\dfrac{d^{2}\theta}{dt^{2}}=f_{2} l \sin \theta – f_{1} l \cos \theta\end{cases}
\(\sin \theta \fallingdotseq \theta,\cos \fallingdotseq 1\)と近似できるので
\begin{cases}f_{1}=m\dfrac{d^{2}}{dt^{2}}(x+l\theta) \\ f_{2}=mg \\ M\dfrac{d^{2}x}{dt^{2}}=f(t)-f_{1} \\ I\dfrac{d^{2}\theta}{dt^{2}}=f_{2} l \theta^{\prime \prime} – f_{1} l\end{cases}
上記から\(f_{1},f_{2},x^{\prime \prime}\)を削除する。第3式と第1式より
\begin{aligned}x^{\prime \prime}&=\dfrac{1}{M}(f(t)-f_{1}) \\ &=\dfrac{1}{M}(f(t)-mx^{\prime \prime}-ml\theta ^{\prime \prime}) \\ &=\dfrac{1}{M+m}(f(t)-ml\theta^{\prime \prime})\end{aligned}
これを(4)の第4式に代入し、ラプラス変換すると
\begin{aligned}I\theta^{\prime \prime}&=mgl\theta-(mx^{\prime \prime}+ml\theta^{\prime \prime}) \\ &=mgl\theta-ml\theta^{\prime \prime} -\dfrac{m}{M+m}(f-ml\theta^{\prime \prime})\end{aligned}
\begin{aligned}Is^{2}=mgl \Theta – mls^{2} \Theta-\dfrac{m}{M+m}F+\dfrac{m^{2}ls^{2}}{M+m} \Theta \end{aligned}
\begin{aligned}\left(Is^{2}+mls^{2}-\dfrac{m^{2}ls^{2}}{M+m}-mgl\right)\Theta=-\dfrac{m}{M+m}F\end{aligned}
\begin{aligned}G(s)=\dfrac{\Theta}{F}=-\dfrac{\dfrac{m}{M+m}}{\left(Is^{2}+mls^{2}-\dfrac{m^{2}ls^{2}}{M+m}-mgl\right)}\end{aligned}
(2)状態方程式
(1)ではラプラス変換しましたが、(2)については微分方程式のまま関係式を導きます。
(4)式を変形し、状態変数の関係を導く
まず、\(\theta^{\prime \prime}\)の関係式を導く。第3式より
\begin{aligned}Mx^{\prime \prime}=f-mx^{\prime \prime}-ml\theta^{\prime \prime}\end{aligned}
\begin{aligned}x^{\prime \prime}=\dfrac{1}{M+m}f-\dfrac{ml}{M+m}\theta^{\prime \prime}\end{aligned}
これを第1式に代入し
\begin{aligned}f_{1}=m\left(\dfrac{1}{M+m}f(t)-\dfrac{ml}{M+m}\theta^{\prime \prime}\right)+ml\theta^{\prime \prime}\end{aligned}
これを第4式に代入し
\begin{aligned}I \theta^{\prime \prime}=mgl\theta – \dfrac{mlf(t)}{M+m}-\dfrac{m^{2}l^{2}}{M+m}\theta^{\prime \prime}+ml^{2}\theta^{\prime \prime}\end{aligned}
\begin{aligned}\left(I+\dfrac{m^{2}l^{2}}{M+m}-ml^{2}\right)\theta^{\prime \prime}=mgl\theta-\dfrac{ml}{M+m}f(t)\end{aligned}
\begin{aligned}\theta^{\prime \prime}=\dfrac{mgl\theta-\dfrac{ml}{M+m}f(t)}{\left(I+\dfrac{m^{2}l^{2}}{M+m}-ml^{2}\right)}\end{aligned}
次に、\(x^{\prime \prime}\)について考える。第3式により
\begin{aligned}Mx^{\prime \prime}=f(t)-mx^{\prime \prime}-ml\theta^{\prime \prime}\end{aligned}
\begin{aligned}\theta^{\prime \prime}=\dfrac{f(t)}{ml}-\dfrac{M+m}{ml}x^{\prime \prime}\end{aligned}
これを第4式に代入し
\begin{aligned}I\left(\dfrac{f(t)}{ml}-\dfrac{M+m}{ml}x^{\prime \prime}\right)=mgl\theta+l(Mx^{\prime \prime}-f(t))\end{aligned}
\begin{aligned}I\left(-\dfrac{M+m}{ml}x^{\prime \prime}-Mlx^{\prime \prime}\right)=mgl\theta-\dfrac{I}{ml}f(t)-lf(t)\end{aligned}
\begin{aligned}x^{\prime \prime}=-\dfrac{mgl\theta-\dfrac{I}{ml}f(t)-lf(t)}{I\left(\dfrac{M+m}{ml}+Ml\right)}\end{aligned}
(15)式、(20)式より、求める状態方程式の行列\(\boldsymbol{A}\)は
\begin{aligned}\boldsymbol{A}=\begin{pmatrix}0 & 1 & 0 & 0 \\ \dfrac{mgl}{\left(I+\dfrac{m^{2}l^{2}}{M+m}-ml^{2}\right)} & 0 &0 &1 \\ 0 & 0 & 0 &0 \\ -\dfrac{mgl}{I\left(\dfrac{M+m}{ml}+Ml\right)} & 0 & 0 &0\end{pmatrix}\end{aligned}
次にベクトル\(\boldsymbol{b}\)は
\begin{aligned}\boldsymbol{b}=\begin{pmatrix}0 \\ \dfrac{-\dfrac{ml}{M+m}}{\left(I+\dfrac{m^{2}l^{2}}{M+m}-ml^{2}\right)} \\ 0 \\ \dfrac{\dfrac{I}{ml}+l}{I\left(\dfrac{M+m}{ml}+Ml\right)}\end{pmatrix}\end{aligned}
\(\theta^{\prime},x^{\prime}\)については関係式が無いため、行列成分には1を入れるだけで良いです。
最後に
式変形があまりにもしんどかったため、計算ミス、記載ミスなどあれば申し訳ございません。そして、こっそり教えて下さると幸いです。