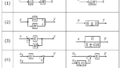
(1)下記のシステムの可観測性を調べよ。なお、状態変数は2次元とする。
\begin{cases}\dot{\boldsymbol{x}(t)}=\begin{pmatrix}0 & 2 \\ 1 & -1 \end{pmatrix}\boldsymbol{x}(t)+\begin{pmatrix}2 \\ -1\end{pmatrix}u(t) \\ y(t)=\begin{pmatrix} 0 & 1 \end{pmatrix}\boldsymbol{x}(t)\end{cases}
(2)上記システムの状態変数\(\boldsymbol{x}(t)\)を、ベクトル\(\boldsymbol{l}=\begin{pmatrix} l_{1} \\ l_{2}\end{pmatrix}\)を用いて推定する。
\begin{aligned}\boldsymbol{\hat{x}}(t)=\boldsymbol{A}\boldsymbol{\hat{x}}(t)+\boldsymbol{b}\boldsymbol{u}(t)-\boldsymbol{l}(\boldsymbol{\hat {y}}(t)-\boldsymbol{y}(t))\end{aligned}
\(\boldsymbol{\hat{x}}(t),\boldsymbol{\hat{y}}(t)\)は、それぞれ\(x(t),y(t)\)の推定値である。推定値と真値の誤差を\(\boldsymbol{e}(t)=\boldsymbol{\hat{x}}(t)-\boldsymbol{x}(t)\)とするとき、状態方程式
\begin{aligned}\boldsymbol{\dot{e}}(t)=\boldsymbol{A_{e}}\boldsymbol{e}(t)\end{aligned}
の行列\(\boldsymbol{A_{e}}\)を\(l_{1},l_{2}\)を用いて表せ。
(3)行列\(\boldsymbol{A_{e}}\)の固有値を-1,-2にする\(\boldsymbol{l}=\begin{pmatrix} l_{1} \\ l_{2}\end{pmatrix}\)を求めよ。
可観測性とは
注目している制御対象の内部状態を計算できること。を言います。以前の記事では、システムの可制御性を説明しました。可制御なシステムは、システムの出力を自由に制御できます。ただし、出力の計算に必要なシステムの内部状態は直接計測できず、出力から計算(推定)する必要があります。任意のシステムで内部状態を計算できるわけではありません。
例として、下記の電気回路を考えます。入力電圧Eが0のとき、出力電圧Vも0になりますが、間のコンデンサにはどのような電圧がかかっているのか不明です。元々電圧がかかっていなかったとすると、出力と同じく電圧0かもしれませんし、以前のどこかのタイミングで充電されていると、0より大きい値を取ります。いずれにせよ、計算(推定)することが出来ません。システムとして不可観測です。
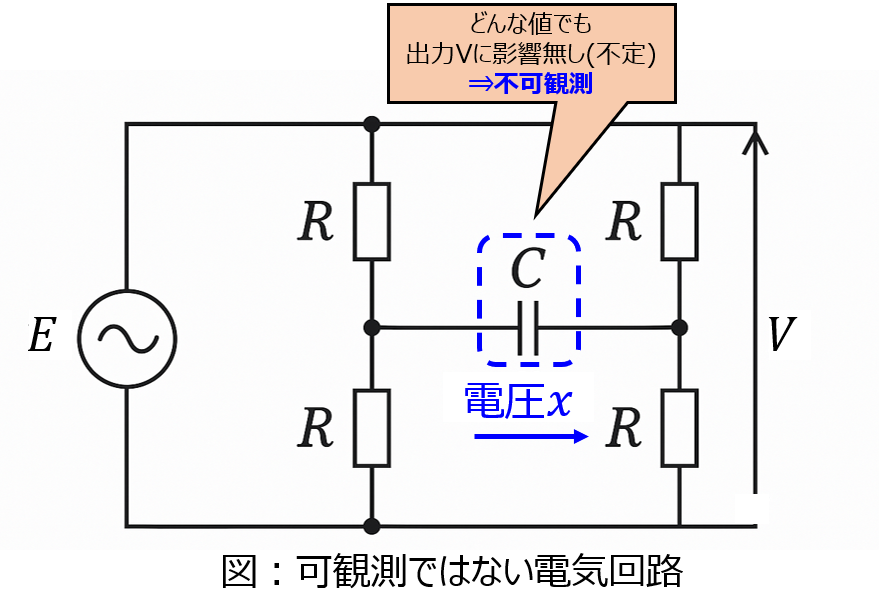
このように、システムには可観測なものと観測できないもの2つが存在します。可観測性は下記の法則で求められます。
l*n次元の可観測性行列\(\boldsymbol{M}=\begin{pmatrix}\boldsymbol{c} \\ \boldsymbol{cA} \\ \vdots \\ \boldsymbol{cA^{n-1}}\end{pmatrix}\)のrankがnであること。
要は、状態方程式の出力に関わる行列\(\boldsymbol{c}\)に\(\boldsymbol{A}\)をn-1次数分かけた値を用いて可観測性行列\(\boldsymbol{M}\)を作成した時、全ての行が線形独立であれば良いです。
詳しい証明については専門書に譲りますが、もし全ての行が線形独立でない場合はどれかの行が線形従属になります。線形従属となった行に関しては、計算が不定となるため状態観測できない。というのが、大まかなイメージです。
状態観測器の極配置
システムが可観測であるとき、可制御の場合と同じように状態観測器の極配置ができます。方針としては、以前の記事と変わらないです。フィードバックベクトルを定義し、状態方程式に代入すると良いです。問題(2)(3)で実際に解いて確認しましょう。
解答例
(1)可観測性の判定
まず、可観測性行列\(\boldsymbol{M}\)は
\begin{aligned}\boldsymbol{cA}=\begin{pmatrix}0 & 1\end{pmatrix}\begin{pmatrix}0 & 2 \\ 1 & -1\end{pmatrix}=\begin{pmatrix}1 & -1\end{pmatrix}\end{aligned}
だから
\begin{aligned}\boldsymbol{M}=\begin{pmatrix}0 & 1 \\ 1 & -1 \end{pmatrix}\end{aligned}
Rank2より可観測
(2)状態方程式の変換
まず、状態方程式は
\begin{cases}\boldsymbol{\dot{x}}(t)=\boldsymbol{A}\boldsymbol{x}(t) + \boldsymbol{b}\boldsymbol{u}(t) \\ y(t)=\boldsymbol{c}\boldsymbol{x}(t)\end{cases}
状態観測器に関する式は
\begin{cases}\boldsymbol{\dot{\hat{x}}}(t)=\boldsymbol{A}\boldsymbol{\hat{x}}(t)+\boldsymbol{b}\boldsymbol{u}(t)-\boldsymbol{l}(\boldsymbol{\hat {y}}(t)-\boldsymbol{y}(t)) \\ \hat{y}(t)=\boldsymbol{c}\boldsymbol{\hat{x}}(t)\end{cases}
推定誤差\(\boldsymbol{e}(t)\)は、\(\boldsymbol{e}(t)=\boldsymbol{\hat{x}}(t) – \boldsymbol{x}(t)\)で表される。これを微分した場合でも同じ関係式になるので、(6式)、(7式)を代入し
\begin{aligned}\boldsymbol{\dot{e}}(t)&=\boldsymbol{A}\boldsymbol{\hat{x}}(t)+\boldsymbol{b}\boldsymbol{u}(t)-\boldsymbol{l}(\boldsymbol{\hat{y}}(t)-\boldsymbol{y}(t))-\boldsymbol{Ax}(t)-\boldsymbol{bu}(t) \\ &=\boldsymbol{A\hat{x}}(t)-\boldsymbol{l}(\boldsymbol{c \hat{x}}(t)-\boldsymbol{cx}(t))-\boldsymbol{Ax}(t) \\ &= (\boldsymbol{A}-\boldsymbol{lc})\boldsymbol{\hat{x}}(t)-(\boldsymbol{A}-\boldsymbol{lc})\boldsymbol{x}(t) \\ &= ( \boldsymbol{A}-\boldsymbol{lc})\boldsymbol{e}(t)\end{aligned}
以上より、求める行列\(\boldsymbol{A_{e}}\)は
\begin{aligned}\boldsymbol{A_{e}}&=\boldsymbol{A}-\boldsymbol{lc} \\ &=\begin{pmatrix}0 & 2 \\ 1 & -1 \end{pmatrix}-\begin{pmatrix}l_{1} \\ l_{2}\end{pmatrix}\begin{pmatrix}0 & 1\end{pmatrix} \\ &=\begin{pmatrix}0 & 2-l_{1} \\ 1 & -1-l_{2}\end{pmatrix}\end{aligned}
(3)行列\(A_{e}\)の固有値
特性方程式を考える
\begin{aligned}|s\boldsymbol{I}-\boldsymbol{A_{e}}|&=\begin{vmatrix}s & -2+l_{1} \\ -1 & s+1+l_{2}\end{vmatrix} \\ &=s(s+1+l_{2})+(-2+l_{1}) \\ &=s^{2}+(1+l_{2})s+(-2+l_{1})\end{aligned}
\(\boldsymbol{A_{e}}\)の固有値が-1,-2のとき、
\begin{aligned}(s+1)(s+2)=s^{2}+3s+2\end{aligned}
となるので、上式を比較して
\begin{cases}l_{1}=4 \\ l_{2}=2 \end{cases}