MOSFET(CMOS)を使用したNAND、NOR回路

論理回路素子の構造

論理回路の勉強をしていると、AND、OR、NOTなる演算子に出くわします。

計算式上では、\(A\cdot A,A+A,\overline{A}\)で表されます。

また、シンボルでは下記のようになっています。

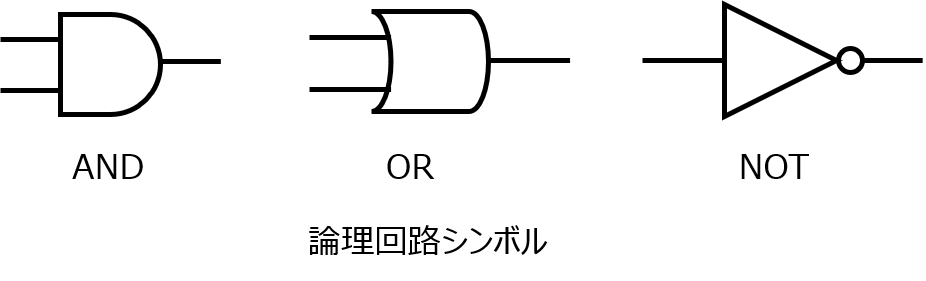
当たり前のように使っている事実ですが、現実にはシンボル通りの素子は無く、何かしらの電気電子回路素子を組み合わせて代用されているはずです。

では、どのような素子を使用しているのでしょうか。

MOSFETが他の回路素子より優れている理由

一番よく使われる素子は、MOSFETです。

理由は電圧制御素子だからです。物理的な接点スイッチや、電流制御素子(バイポーラトランジスタ)を用いる別の手法に対して下記のメリットがあります。

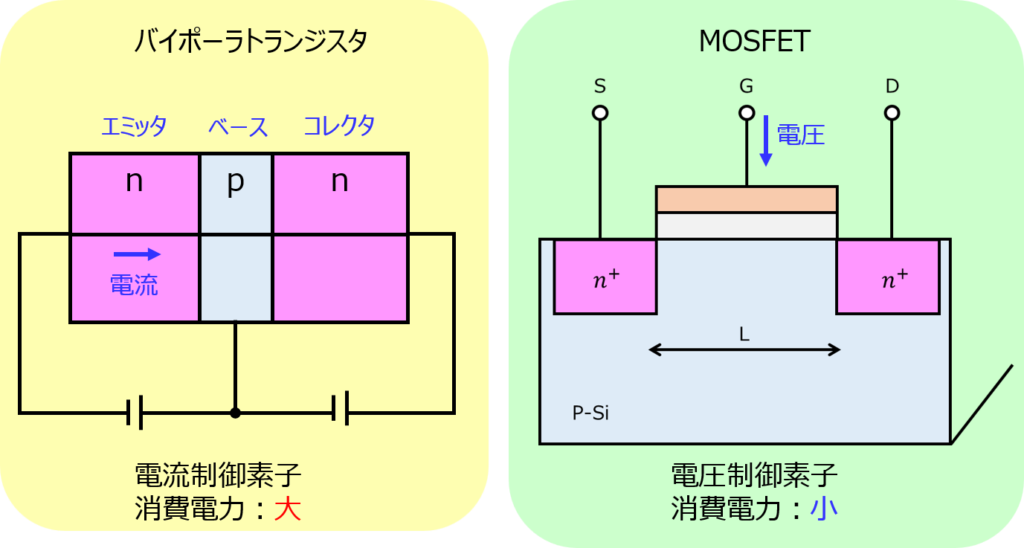
１．については文言通りです。MOSFETは、端子に電圧を印可する/しないで制御するため、物理接点を考えなくて良いです。

２．については、消費電力の式\(P=RI^{2}\)で説明します。電流制御素子は、その名の通り電流制御するため、電圧制御素子に対して大電流が流れます。そのため、上式の電流の二乗が効いて、消費電力が大きくなります。

一方で、電圧制御素子は、電圧を利用するため電流はあまり流れません。よって、消費電力を低減できます。

その他、電圧制御素子は、電流制御素子に対して動作が高速である特性もあります。

PC、家庭用家電など、大電力を消費しない機器ではよく使用されます。

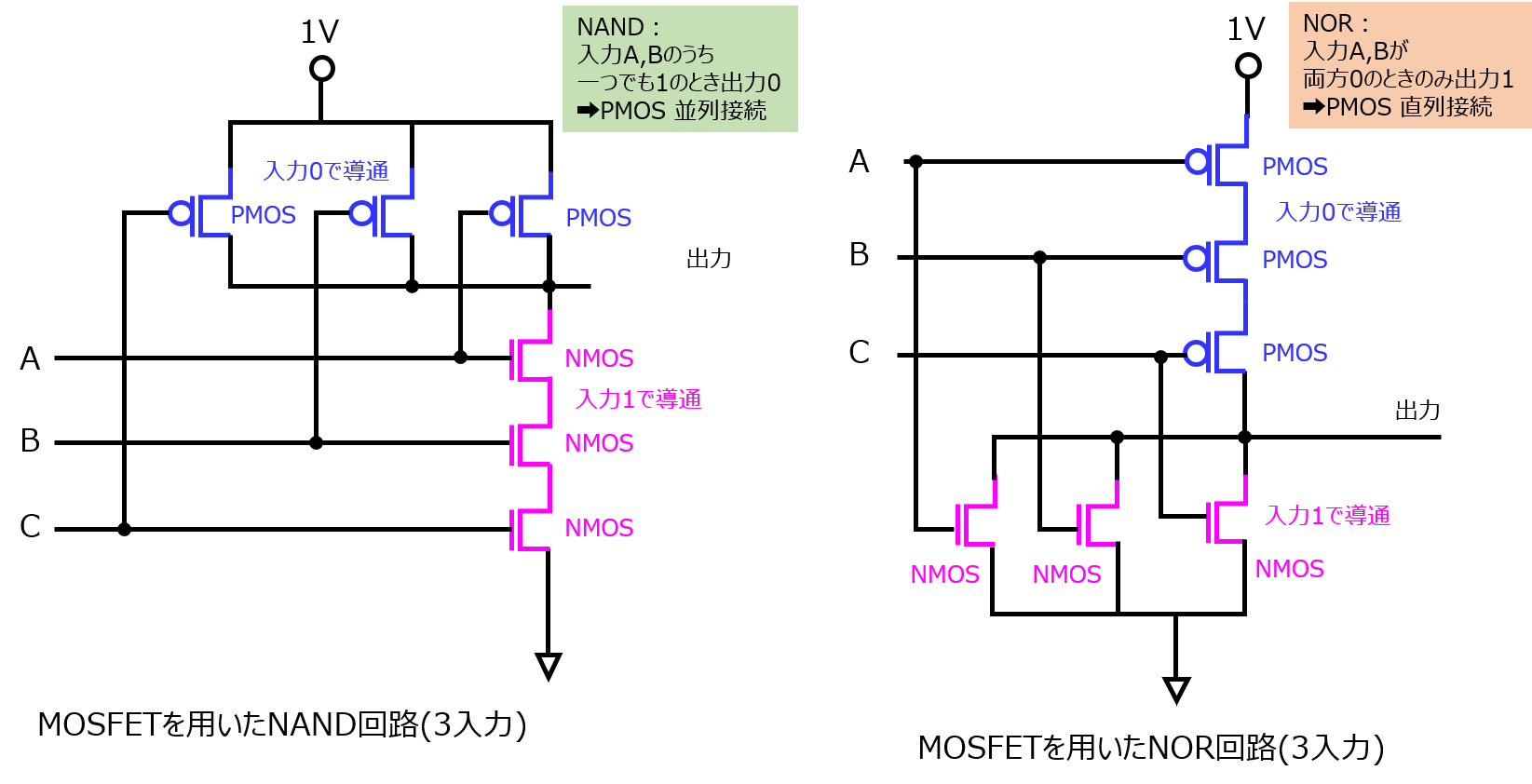
MOSFETを利用した論理回路の構成

入力電圧が所定値以下のとき、1を出力する(導通する)PMOS

入力電圧が所定値以上のとき、1を出力する(導通する)NMOS

以上2つの素子を1つずつ組み合わせて構成します。

PMOSとNMOSの組み合わせ回路を、CMOS(Complementary MOS)と呼びます。

半導体デバイスで出てくるMOSFETは、一般的にNMOSを指しています。PMOSのシンボルは、MOSFETのゲートの入力に〇を付けます。(下図)

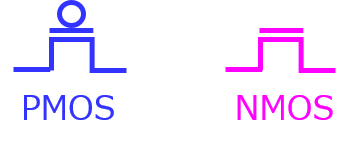
完全系の記事で説明した通り、全ての論理演算は、NAND、NORで表現できます。

ですので、CMOSもNAND、NORを表すように考えます。

MOSFETを利用したNAND回路

一般的に、MOSFETを論理回路として利用するときは、電源(正)を上に、GNDを下に書きます。

また、PMOSを上に、NMOSを下に書きます。

PMOSのラインのうち、一つでもGND側へ導通していれば1を出力し、導通ラインが無ければ0を出力します。

まず、2入力NANDの構成を示します。

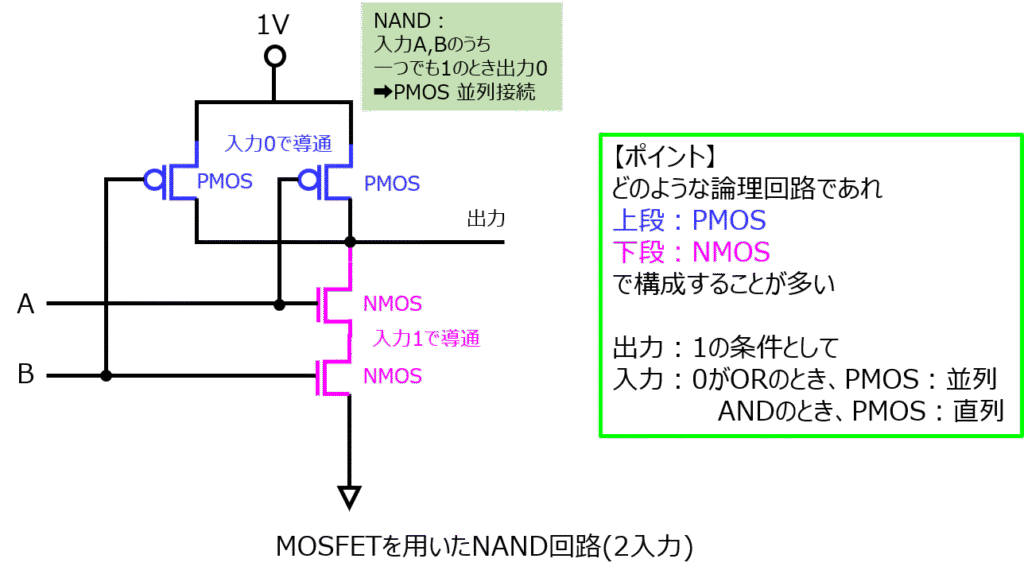
NANDは、入力が全て1の時以外は出力1になります。

言い換えると、一つでも入力が0のときは出力1になります。

よって、入力が0の場合導通するPMOSのラインは並列とし、NMOSのラインは反対に直列とします。

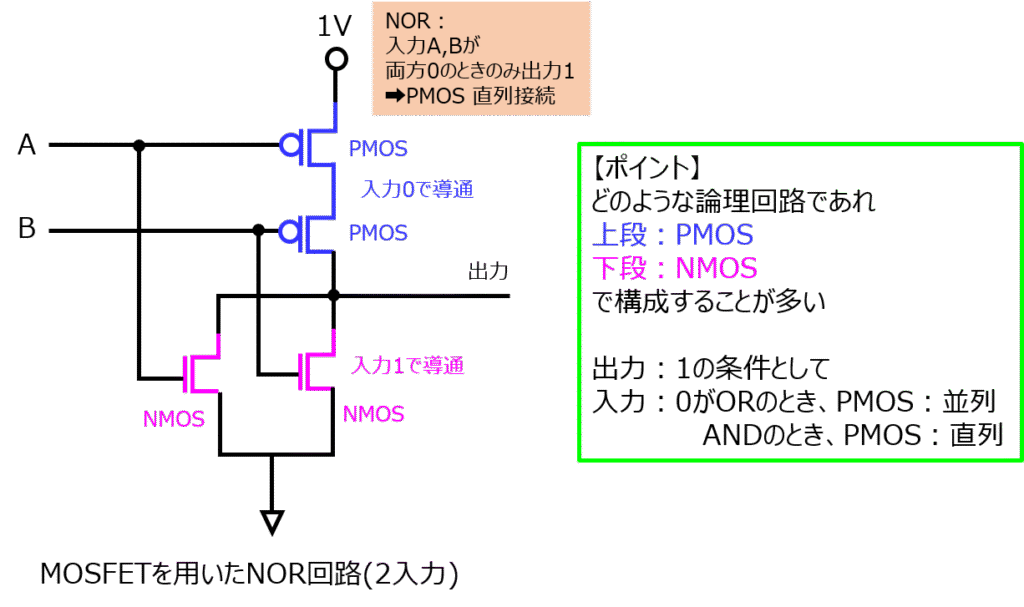
MOSFETを使用したNOR回路

NANDと逆に、入力が全て0のときは出力1になります。

これを回路で表現すると、0で導通するPMOSを全て直列したとき、出力ラインに繋がる構成になります。

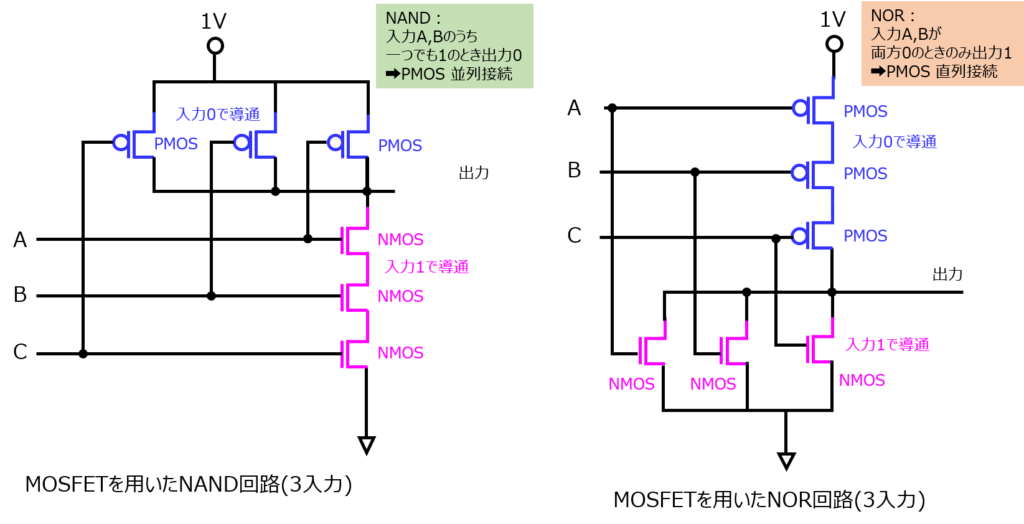
3入力NAND、NOR回路

本章で説明した考え方は3入力以上でも同じです。入力数が増えた分、並列にするPMOSの数を増やし、直列にするNMOSの数を同じく増やせば良いです。

複合ゲートを利用したMOSFET数の低減

前章で、NAND、NORの構成を説明しました。

シャノンの展開定理により、全ての論理式はNAND、NORで表現できます。

よって、前章で説明した回路を組み合わせることで任意の論理式を表現できます。

この時、使用するMOSFET数が増加する課題があります。なるべく低減したいと考えます。

ここで、複合ゲートの考え方を使用します。

AOI複合ゲート

AND-OR-Intert回路の略です。

3入力A,B,Cに対する出力\begin{aligned}Y=\overline{A \cdot B+C}\end{aligned}を考えます。

ドモルガン律により、\begin{aligned}Y=\overline{\overline{\overline{A \cdot B}}+C}\end{aligned}になります。前章の考え方を用いて回路を表すと、下記になります。

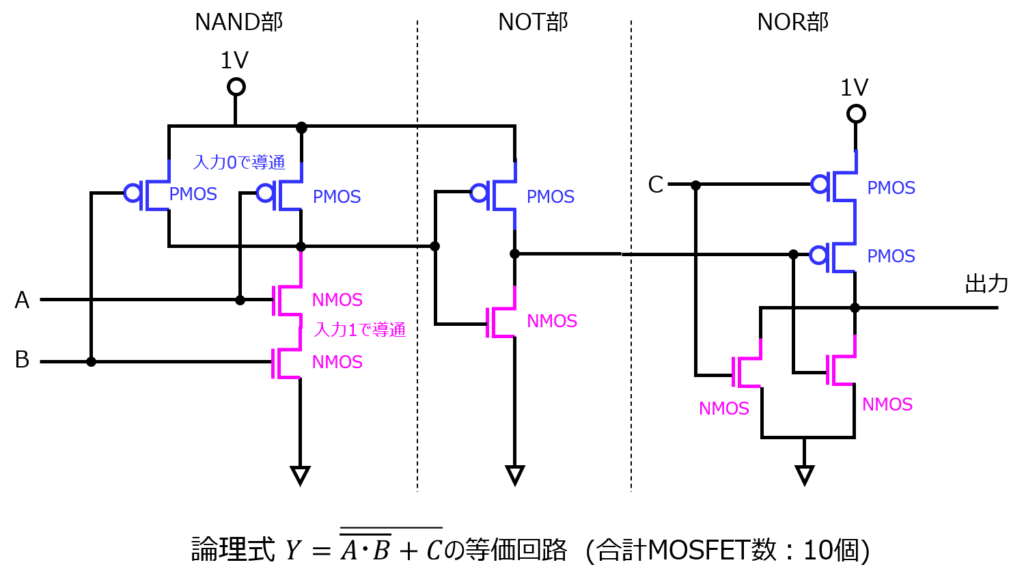
NOR(A,B)の部分でMOSFET4つ、NOTの部分でMOSFET2つ、NAND(A,B)の部分でMOSFET4つと、合計10個必要です。

これをAOI複合ゲートで表すこと、下記になります。

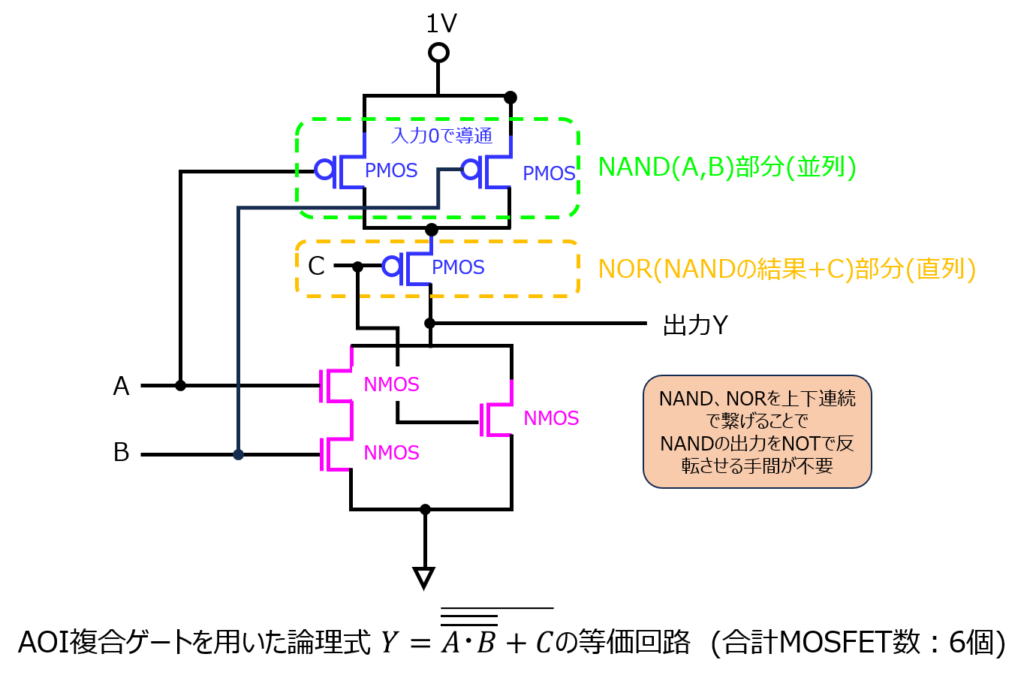
(1)式を左から見るとNAND➡NORの順に続きますので、この通りに上から回路を組んでいます。

※NANDの上にNOTが余分に付いていますが、(2)式よりNOTは打ち消し合うので結局出力には影響しないイメージです。

このように、与えられた論理式をNAND,NORで表現できれば、後は上から順にブロックで並べていくと等価回路を表現できます。

OAI複合ゲート

OR-ANDの順でInvertする回路をOAI複合ゲートと言います。

前節のように、3入力A,B,Cに対する出力\begin{aligned}Y=\overline{(A + B) \cdot C}\end{aligned}を考えます。

同じく、ドモルガン律を用いると\begin{aligned}Y=\overline{\overline{\overline{A + B}} \cdot C}\end{aligned}

になり、式の通りにMOSFETを組むと10個必要ですが、A+B, ・Cをブロックとして見ると

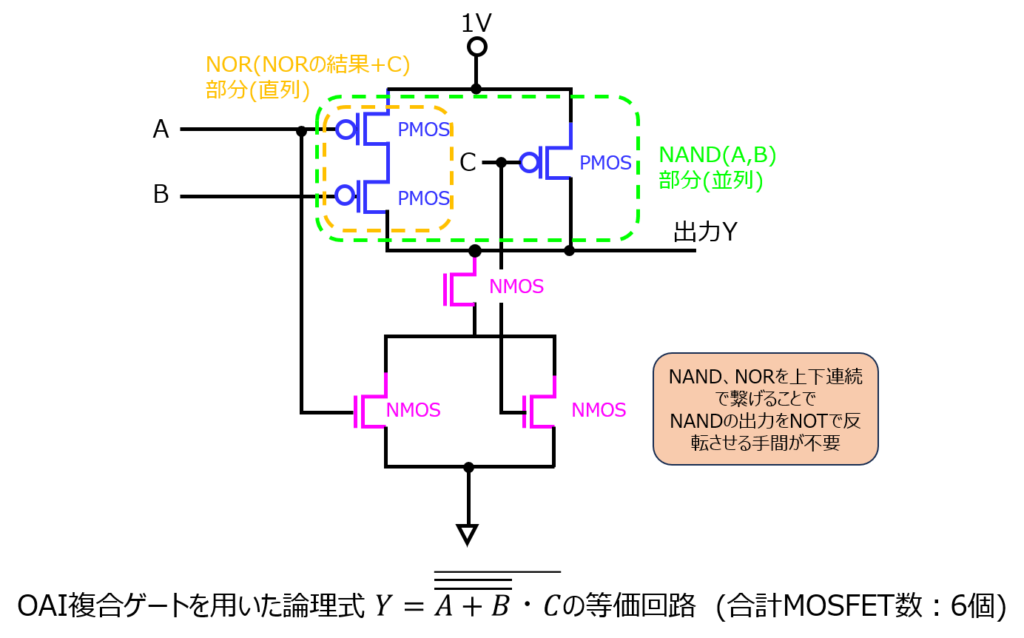
と同じくMOSFET6個で表すことができました。

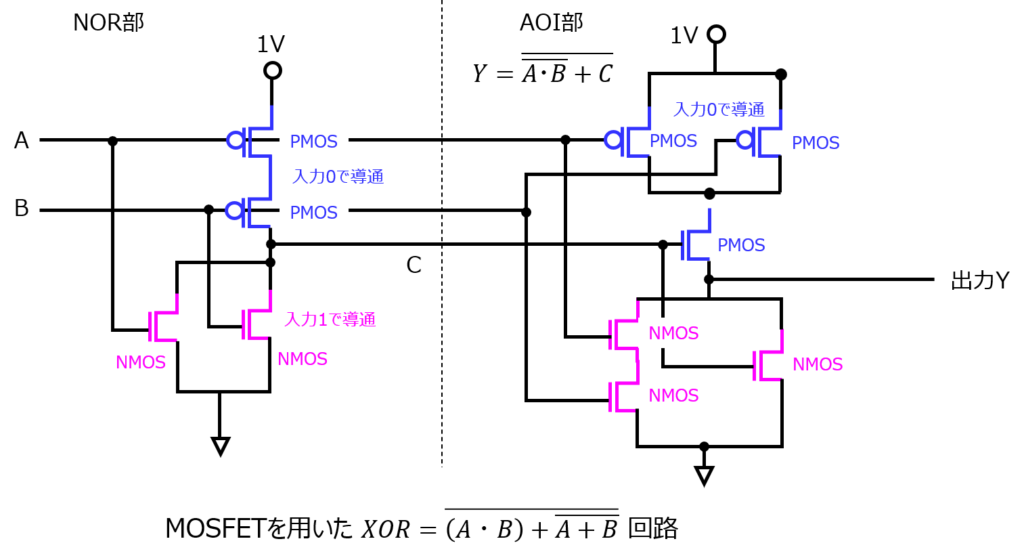
複合ゲートを利用したXORの表記

XOR：排他的論理和は、\(Y=A \cdot \overline{B}+\overline{A} \cdot B\)と表せます。

これをドモルガン律を利用すると、

\begin{aligned}Y=\overline{(A\cdot B)+\overline{A+B}}\end{aligned}

と表せます。これをAOI複合ゲートを用いて表現することを考えます。

まず、(5)式の第2項\(\overline{A + B}\)は普通にPMOS,NMOS2個ずつで表します。

この出力をCとすると、

\begin{aligned}Y=\overline{C+\overline{A+B}}\end{aligned}

となるので、AOI複合ゲートの論理式通りになります。

よって、(5)式はNORとAOI複合ゲートの2段で表すことができるので、下記になります。

補足

複合ゲートの方が、論理式通りにMOSFETを繋げた場合と比較して高周波で動作できます。また、消費電力も少ないです。

これは、使用するMOSFET数が少ないためです。

最後に

PMOS、NMOSを用いたディジタル電子回路設計は、神戸大学、京都工芸繊維大学の院試でよく見られます。

本記事の内容を理解し、試験会場で問題を解き進める一つの要素になれば幸いです。

参考文献

OHM大学テキスト 集積回路工学 吉本雅彦(編著) P42-53